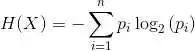譯者 | 趙青窕

審校 | 孫淑娟

前言

在機器學習中，分類具有兩個階段，分別是學習階段和預測階段。在學習階段，基于給定的訓練數據建立模型；在預測階段，該模型用于預測給定數據的響應。決策樹是最容易理解和解釋的分類算法之一。

在機器學習中，分類具有兩個階段，分別是學習階段和預測階段。在學習階段，基于給定的訓練數據建立模型；在預測階段，該模型用于預測給定數據的響應。決策樹是最容易理解和解釋的分類算法之一。

決策樹算法

決策樹算法屬于監督學習算法中的一種。與其他監督學習算法不同，決策樹算法可以用于解決回歸和分類問題。

使用決策樹的目的是創建一個訓練模型，通過學習從之前的數據（訓練數據）推斷出的簡單決策規則來預測目標變量的類或值。

在決策樹中，我們從樹的根開始來預測一個記錄的類標簽。我們將根屬性的值與記錄的屬性進行比較，在比較的基礎上，我們跟隨該值對應的分支并跳轉到下一個節點。

決策樹的類型

基于我們所擁有的目標變量的類型，我們可以把樹分為兩種類型:

1.分類變量決策樹：有一個分類目標變量的決策樹，稱為分類變量決策樹。

2.連續變量決策樹：決策樹的目標變量是連續的，因此稱為連續變量決策樹。

例子：假設我們有一個預測客戶是否會向保險公司支付續期保費的問題。這里客戶的收入是一個重要的變量，但保險公司沒有所有客戶的收入細節。現在，我們知道這是一個重要的變量，然后我們可以建立一個決策樹，基于職業，產品和其他各種變量來預測客戶的收入。在這種情況下，我們預測目標變量是連續的。

與決策樹相關的重要術語

1.根節點(root node)：它代表整個成員或樣本，這些成員或樣本會進一步被分成兩個或多個同類型的集合。

2.分離Splitting)：將一個節點拆分為兩個或多個子節點的過程。

3.決策節點(Decision Node)：當一個子節點分裂成更多的子節點時，它被稱為決策節點。

4.葉子/終端節點(Leaf / Terminal Node)：不可拆分的節點稱為葉子或終端節點。

5.修剪(Pruning)：我們刪除一個決策節點的子節點的過程被稱為修剪。也可以把修建看作是分離的反過程。

6.分支/子樹(Branch / Sub-Tree)：整個樹的一個子部分稱為分支或子樹。

7.父節點和子節點(Parent and Child Node)：節點可以拆分出子節點的節點稱為父節點，子節點是父節點的子節點。

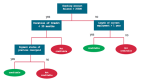
決策樹通過從根到葉/終端節點的降序方式來對樣本進行分類，葉/終端節點提供樣品的分類方式。樹中的每個節點都充當某個屬性的測試用例，從節點的每個降序方向都對應著測試用例的可能答案。這個過程本質上是遞歸的過程，并且對每個在新節點上扎根的子樹采用相同的處理方式。

創建決策樹時所進行的假設

以下是我們在使用決策樹時所做的一些假設:

●首先，將整個訓練集作為根。

●特征值最好是可以分類的。如果這些值是連續的，那么在建立模型之前可以對它們進行離散化處理。

●記錄是基于屬性值遞歸分布的。

●通過使用一些統計方法來把相應屬性按順序放置在樹的根節點或者樹的內部節點。

決策樹遵循乘積和表述形式。乘積和(SOP)也被稱為析取范式。對于一個類，從樹根到具有相同類的葉節點的每個分支都是值的合取，在該類中結束的不同分支構成了析取。

決策樹實現過程中的主要挑戰是確定根節點及每一級節點的屬性，這個問題就是屬性選擇問題。目前有不同的屬性選擇方法來選擇每一級節點的屬性。

決策樹是如何工作的?

決策的分離特性嚴重影響樹的準確性，分類樹和回歸樹的決策標準不同。

決策樹使用多種算法來決定將一個節點分成兩個或多個子節點。子節點的創建增加了子節點的同質性。換句話說，相對于目標變量來說，節點的純度增加了。決策樹將所有可用變量上的節點進行分離，然后選擇可以產生很多同構子節點的節點進行拆分。

算法是基于目標變量的類型進行選擇的。接下來，讓我們看一看決策樹中會使用到的一些算法:

ID3→(D3的延伸)

C4.5→(ID3的繼承者)

CART→(分類與回歸樹)

CHAID→(卡方自動交互檢測(Chi-square automatic interaction detection)在計算分類樹時進行多級分離)

MARS→(多元自適應回歸樣條)

ID3算法使用自頂向下的貪婪搜索方法，在不回溯的情況下，通過可能的分支空間構建決策樹。貪婪算法，顧名思義，總是某一時刻做出似乎是最好的選擇。

ID3算法步驟:

1.它以原始集合S作為根節點。

2.在算法的每次迭代過程中，對集合S中未使用的屬性進行迭代，計算該屬性的熵(H)和信息增益(IG)。

3.然后選擇熵最小或信息增益最大的屬性。

4.緊接著用所選的屬性分離集合S以產生數據的子集。

5.該算法繼續在每個子集上迭代，每次迭代時只考慮以前從未選擇過的屬性。

屬性選擇方法

如果數據集包含N個屬性，那么決定將哪個屬性放在根節點或放在樹的不同級別作為內部節點是一個復雜的步驟。通過隨機選擇任意節點作為根結點并不能解決問題。如果我們采用隨機的方法，可能會得到比較糟糕的結果。

為了解決這一屬性選擇問題，研究人員設計了一些解決方案。他們建議使用如下標準:

• 熵
• 信息增益
• 基尼指數
• 增益率
• 方差削減
• 卡方

使用這些標準計算每個屬性的值，然后對這些值進行排序，并將屬性按照順序放置在樹中，也就是說，高值的屬性放置在根位置。

在使用信息增益作為標準時，我們假設屬性是分類的，而對于基尼指數，我們假設屬性是連續的。

1. 熵

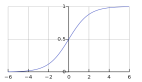
熵是對被處理信息的隨機性的度量。熵值越高，就越難從信息中得出任何結論。拋硬幣就是提供隨機信息的行為的一個例子。

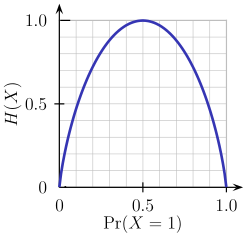
由上圖可知，當概率為0或1時，熵H(X)為零。當概率為0.5時，熵是最大的，因為它在數據中投射出完全的隨機性。

ID3遵循的規則是：一個熵為0的分支是一個葉節點，一個熵大于0的分支需要進一步分離。

單個屬性的數學熵表示如下:

其中S表示當前狀態，Pi表示狀態S中事件i的概率或狀態S節點中i類的百分比。

多個屬性的數學熵表示如下:

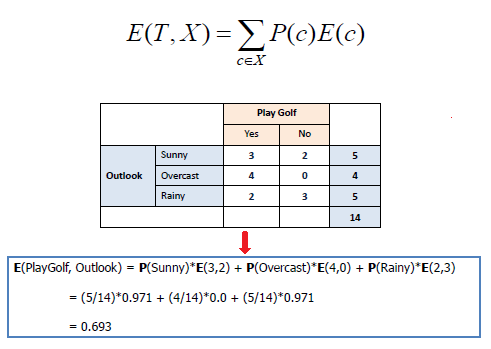
其中T表示當前狀態，X表示選定屬性

2.信息增益

信息增益(Information gain, IG)是一種統計屬性，用來衡量給定屬性根據目標類分離訓練的效果。構建決策樹就是尋找一個返回最高信息增益和最小熵的屬性的過程。

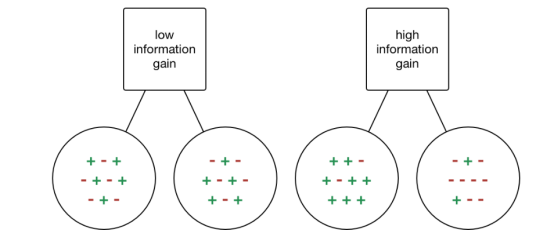
信息的增加就是熵的減少。它根據給定的屬性值計算數據集分離前的熵差和分離后的平均熵差。ID3決策樹算法使用的就是信息增益的方法。

IG在數學上表示如下:

用一種更簡單的方法，我們可以得出這樣的結論:

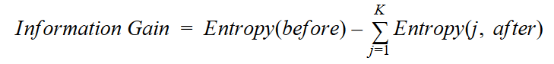
其中before為拆分前的數據集，K為拆分產生的子集數量，(j, after)為拆分后的子集j。

3.基尼指數

您可以將基尼指數理解為用于評估數據集中分離的成本函數。它的計算方法是用1減去每個類的概率平方和。它傾向于較大的分區并且易于實現的情形，而信息增益則傾向于具有不同值的較小分區的情形。

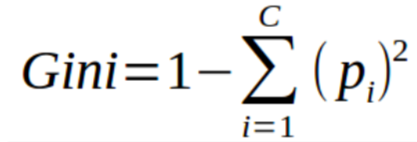
基尼指數離不開分類目標變量“成功”或“失敗”。它只執行二進制分離。基尼系數越高，不平等程度越高，異質性越強。

計算基尼指數分離的步驟如下：

• 計算子節點的基尼系數，使用上面的成功(p)和失敗(q)的公式(p2+q2)。
• 使用分離的每個節點的加權基尼得分計算分離的基尼系數指數。

CART(Classification and Regression Tree)就是使用基尼指數方法來創建分離點。

4.增益率

信息增益傾向于選擇具有大量值的屬性作為根節點。這意味著它更喜歡具有大量不同值的屬性。

C4.5是ID3的改進方法，它使用增益比，這是對信息增益的一種修正，以減少其偏置，通常是最好的選擇方法。增益率克服了信息增益的問題，在進行拆分之前考慮了分支的數量。它通過考慮分離的內在信息來糾正信息增益。

假如我們有一個數據集，其中包含用戶和他們的電影類型偏好，這些偏好基于性別、年齡組、等級等變量。在信息增益的幫助下，你將在“性別”中進行分離(假設它擁有最高的信息增益)，現在變量“年齡組”和“評級”可能同樣重要，在增益比的幫助下，我們可以選擇在下一層中進行分離的屬性。

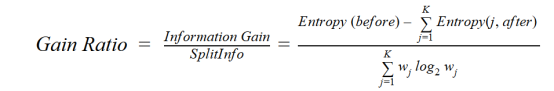
其中before為分離前的數據集，K為分離產生的子集數量，(j, after)為分離后的子集j。

5.方差削減

方差削減是一種用于連續目標變量(回歸問題)的算法。該算法使用標準方差公式來選擇最佳分離方式。選擇方差較低的分離作為分離總體的標準:

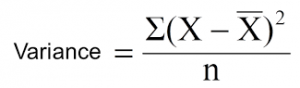
是均值，X是實際值，n是值的個數。

計算方差的步驟:

• 計算每個節點的方差。
• 計算每一次分離的方差并作為每個節點方差的加權平均。

6.卡方

CHAID是Chi-squared Automatic Interaction Detector的縮寫。這是比較老的樹的分類方法之一。找出子節點與父節點之間的差異具有統計學意義。我們通過對目標變量的觀測頻率和期望頻率之間的標準化差的平方和來衡量它。

它與分類目標變量“成功”或“失敗”一起工作。它可以執行兩次或多次分離。卡方值越高，子節點與父節點之間的差異統計意義就越高。它生成一個名為CHAID的樹。

在數學上，Chi-squared表示為:

計算卡方的步驟如下:

• 通過計算成功和失敗的偏差來計算單個節點的卡方
• 使用分離的各節點的成功和失敗的所有卡方之和計算分離的卡方

如何避免/對抗決策樹的過擬合(Overfitting)?

決策樹存在一個常見問題，特別是對于一個滿列的樹。有時它看起來像是樹記住了訓練數據集。如果一個決策樹沒有限制，它會給你100%的訓練數據集的準確性，因為在最糟糕的情況下，它最終會為每個觀察產生一個葉子。因此，當預測不屬于訓練集的樣本時，這就會影響準確性。

在此我介紹兩種方法來消除過擬合，分別是修剪決策樹和隨機森林。

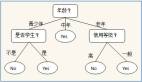
1.修剪決策樹

分離過程會產生完全長成的樹，直到達到停止標準。但是，成熟的樹很可能會過度擬合數據，導致對未見數據的準確性較差。

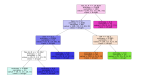
在修剪中，你剪掉樹的分支，也就是說，刪除從葉子節點開始的決策節點，這樣整體的準確性就不會受到干擾。這是通過將實際的訓練集分離為兩個集：訓練數據集D和驗證數據集V，用分離的訓練數據集D準備決策樹，然后繼續對樹進行相應的修剪，以優化驗證數據集V的精度。

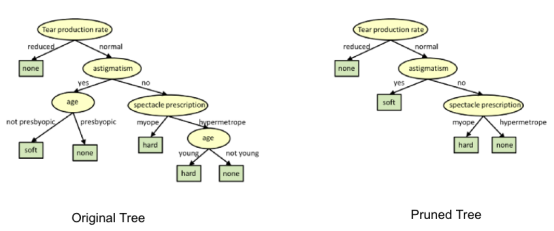
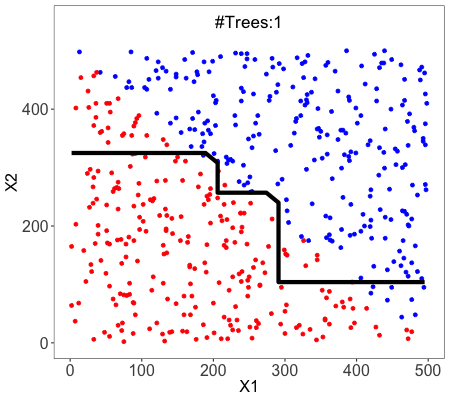
在上圖中，樹左側的“Age”屬性已經被修剪，因為它在樹的右側更重要，因此消除了過擬合。

2.隨機森林

隨機森林是集成學習(Ensemble Learning)的一個例子，我們結合多種機器學習算法來獲得更好的預測性能。因為構建樹時訓練數據集是隨機抽樣的，且分離節點時考慮特征的隨機子集，所以我們把這種方法稱之為隨機。

一種被稱為bagging的技術被用來創建一個樹的集合，其中多個訓練集通過替換生成。

bagging技術采用隨機抽樣的方法將數據集劃分為N個樣本。然后，使用單一學習算法在所有樣本上建立模型。之后通過并行投票或平均的方式將預測結果結合起來。

線性模型和基于樹的模型哪個更好?

該問題取決于你要解決的問題類型。

1.如果因變量和自變量之間的關系可以被一個線性模型很好地模擬，線性回歸將優于基于樹的模型。

2.如果因變量和自變量之間存在高度的非線性且復雜的關系，樹模型將優于經典回歸方法。

3.如果你需要建立一個容易理解的模型，決策樹模型總是比線性模型更好。決策樹模型比線性回歸更容易理解!

使用Scikit-learn進行決策樹分類器構建

我采用的數據是從https://drive.google.com/open?id=1x1KglkvJxNn8C8kzeV96YePFnCUzXhBS下載的超市相關數據，首先使用下面的代碼加載所有基本庫：

import numpy as np
import matplotlib.pyplot as plt 
import pandas as pd

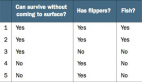
之后，我們采用下面的方式加載數據集。它包括5個屬性，用戶id，性別，年齡，預估工資和購買情況。

data = pd.read_csv('/Users/ML/DecisionTree/Social.csv')
data.head()

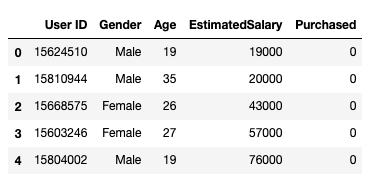
圖1數據集

我們只將年齡和預估工資作為我們的自變量X，因為性別和用戶ID等其他特征是不相關的，對一個人的購買能力沒有影響，y是因變量。

feature_cols = ['Age','EstimatedSalary' ]X = data.iloc[:,[2,3]].values
y = data.iloc[:,4].values

下一步是將數據集分離為訓練集和測試集。

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test =  train_test_split(X,y,test_size = 0.25, random_state= 0)

接下來執行特征縮放

#feature scaling
from sklearn.preprocessing import StandardScaler
sc_X = StandardScaler()
X_train = sc_X.fit_transform(X_train)
X_test = sc_X.transform(X_test)

將模型擬合到決策樹分類器中。

from sklearn.tree import DecisionTreeClassifier
classifier = DecisionTreeClassifier()
classifier = classifier.fit(X_train,y_train)

進行預測并檢查準確性。

#prediction
y_pred = classifier.predict(X_test)#Accuracy
from sklearn import metricsprint('Accuracy Score:', metrics.accuracy_score(y_test,y_pred))

決策樹分類器的準確率達到91%。

混淆矩陣

from sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred)Output:
array([[64,  4],
       [ 2, 30]])

這意味著有6個觀測結果被列為錯誤。

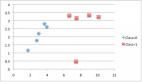
首先，讓我們將模型預測結果可視化

from matplotlib.colors import ListedColormap
X_set, y_set = X_test, y_test
X1, X2 = np.meshgrid(np.arange(start = X_set[:,0].min()-1, stop= X_set[:,0].max()+1, step = 0.01),np.arange(start = X_set[:,1].min()-1, stop= X_set[:,1].max()+1, step = 0.01))
plt.contourf(X1,X2, classifier.predict(np.array([X1.ravel(), X2.ravel()]).T).reshape(X1.shape), alpha=0.75, cmap = ListedColormap(("red","green")))plt.xlim(X1.min(), X1.max())
plt.ylim(X2.min(), X2.max())for i,j in enumerate(np.unique(y_set)):
    plt.scatter(X_set[y_set==j,0],X_set[y_set==j,1], c = ListedColormap(("red","green"))(i),label = j)
plt.title("Decision Tree(Test set)")
plt.xlabel("Age")
plt.ylabel("Estimated Salary")
plt.legend()
plt.show()

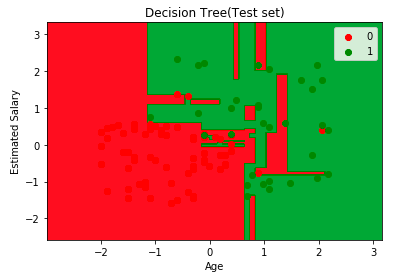
接下來，想象一下這棵樹

接下來您可以使用Scikit-learn的export_graphviz函數在Jupyter筆記本中顯示樹。為了繪制樹，我們需要采用下面的命令安裝Graphviz和pydotplus：

conda install python-graphviz
pip install pydotplus

export_graphviz函數將決策樹分類器轉換為點文件，pydotplus將該點文件轉換為png或在Jupyter上顯示的形式，具體實現方式如下：

from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO  
from IPython.display import Image  
import pydotplusdot_data = StringIO()
export_graphviz(classifier, out_file=dot_data,  
                filled=True, rounded=True,
                special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())  
Image(graph.create_png())

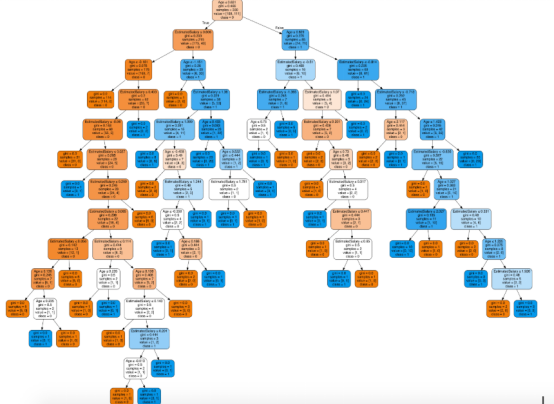
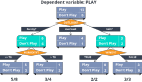
在決策樹形圖中，每個內部節點都有一個分離數據的決策規則。Gini代表基尼系數，它代表了節點的純度。當一個節點的所有記錄都屬于同一個類時，您可以說它是純節點，這種節點稱為葉節點。

在這里，生成的樹是未修剪的。這棵未經修剪的樹不容易理解。在下一節中，我會通過修剪的方式來優化樹。

隨后優化決策樹分類器

criteria: 該選項默認配置是Gini，我們可以通過該項選擇合適的屬性選擇方法，該參數允許我們使用different-different屬性選擇方式。支持的標準包含基尼指數的“基尼”和信息增益的“熵”。

splitter: 該選項默認配置是" best "，我們可以通過該參數選擇合適的分離策略。支持的策略包含“best”(最佳分離)和“random”(最佳隨機分離)。

max_depth：默認配置是None，我們可以通過該參數設置樹的最大深度。若設置為None，則節點將展開，直到所有葉子包含的樣本小于min_samples_split。最大深度值越高，過擬合越嚴重，反之，過擬合將不嚴重。

在Scikit-learn中，只有通過預剪枝來優化決策樹分類器。樹的最大深度可以用作預剪枝的控制變量。

# Create Decision Tree classifer object
classifier = DecisionTreeClassifier(criterion="entropy", max_depth=3)# Train Decision Tree Classifer
classifier = classifier.fit(X_train,y_train)#Predict the response for test dataset
y_pred = classifier.predict(X_test)# Model Accuracy, how often is the classifier correct?
print("Accuracy:",metrics.accuracy_score(y_test, y_pred))

至此分類率提高到94%，相對之前的模型來說，其準確率更高。現在讓我們再次可視化優化后的修剪后的決策樹。

dot_data = StringIO()
export_graphviz(classifier, out_file=dot_data,  
                filled=True, rounded=True,
                special_characters=True, feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())  
Image(graph.create_png())

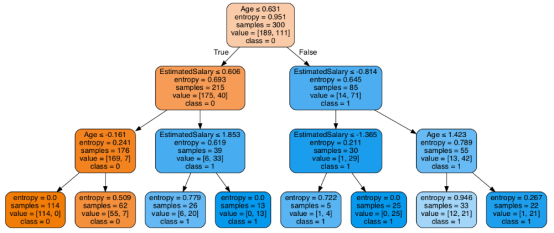
上圖是經過修剪后的模型，相對之前的決策樹模型圖來說，其更簡單、更容易解釋和理解。

總結

在本文中，我們討論了很多關于決策樹的細節，它的工作方式，屬性選擇措施，如信息增益，增益比和基尼指數，決策樹模型的建立，可視化，并使用Python Scikit-learn包評估和優化決策樹性能，這就是這篇文章的全部內容，希望你們能喜歡它。

譯者介紹

趙青窕，51CTO社區編輯，從事多年驅動開發。

原文標題：??Decision Tree Algorithm, Explained??，作者：Nagesh Singh Chauhan