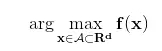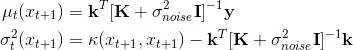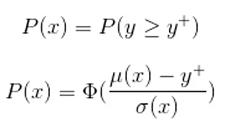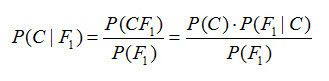擬合目標函數后驗分布的調參利器:貝葉斯優化
如何優化機器學習的超參數一直是一個難題,我們在模型訓練中經常需要花費大量的精力來調節超參數而獲得更好的性能。因此,貝葉斯優化利用先驗知識逼近未知目標函數的后驗分布從而調節超參數就變得十分重要了。本文簡單介紹了貝葉斯優化的基本思想和概念,更詳細的推導可查看文末提供的論文。
超參數
超參數是指模型在訓練過程中并不能直接從數據學到的參數。比如說隨機梯度下降算法中的學習速率,出于計算復雜度和算法效率等,我們并不能從數據中直接學習一個比較不錯的學習速度。但學習速率卻又是十分重要的,較大的學習速率不易令模型收斂到較合適的較小值解,而較小的學習速率卻又常常令模型的訓練速度大大降低。對于像學習速率這樣的超參數,我們通常需要在訓練模型之前設定。因此,對于超參數眾多的復雜模型,微調超參數就變得十分痛苦。
超參數的選擇同樣對深度神經網絡十分重要,它能大大提高模型的性能和精度。尋找優良的超參數通常需要解決這兩個問題:
- 如何高效地搜索可能的超參數空間,在實踐中至少會有一些超參數相互影響。
- 如何管理調參的一系列大型試驗。
簡單的調參法
在介紹如何使用貝葉斯優化進行超參數調整前,我們先要了解調參的樸素方法。
執行超參數調整的傳統方法是一種稱之為網格搜索(Grid search)的技術。網格搜索本質上是一種手動指定一組超參數的窮舉搜索法。假定我們的模型有兩個超參數 learning_rate 和 num_layes,表格搜索要求我們創建一個包含這兩個超參數的搜索表,然后再利用表格中的每一對(learning_rate,num_layes)超參數訓練模型,并在交叉驗證集或單獨的驗證集中評估模型的性能。網格搜索***會將獲得***性能的參數組作為***超參數。
網格搜索窮舉地搜索整個超參數空間,它在高維空間上并不起作用,因為它太容易遇到維度災難了。而對于隨機搜索來說,進行稀疏的簡單隨機抽樣并不會遇到該問題,因此隨機搜索方法廣泛地應用于實踐中。但是隨機搜索并不能利用先驗知識來選擇下一組超參數,這一缺點在訓練成本較高的模型中尤為突出。因此,貝葉斯優化能利用先驗知識高效地調節超參數。
貝葉斯優化的思想
貝葉斯優化是一種近似逼近的方法。如果說我們不知道某個函數具體是什么,那么可能就會使用一些已知的先驗知識逼近或猜測該函數是什么。這就正是后驗概率的核心思想。本文的假設有一系列觀察樣本,并且數據是一條接一條地投入模型進行訓練(在線學習)。這樣訓練后的模型將顯著地服從某個函數,而該未知函數也將完全取決于它所學到的數據。因此,我們的任務就是找到一組能***化學習效果的超參數。
具體來說在 y=mx+c 中,m 和 c 是參數,y 和 x 分別為標注和特征,機器學習的任務就是尋找合適的 m 和 c 構建優秀的模型。
貝葉斯優化可以幫助我們在眾多模型中選取性能***的模型。雖然我們可以使用交叉驗證方法尋找更好的超參數,但是我們不知道需要多少樣本才能從一些列候選模型中選出性能***的模型。這就是為什么貝葉斯方法能通過減少計算任務而加速尋找***參數的進程。同時貝葉斯優化還不依賴于人為猜測所需的樣本量為多少,這種***化技術是基于隨機性和概率分布而得出的。
簡單來說,當我們饋送***個樣本到模型中的時候,模型會根據該樣本點構建一個直線。饋送第二個樣本后,模型將結合這兩個點并從前面的線出發繪制一條修正線。再到第三個樣本時,模型繪制的就是一條非線性曲線。當樣本數據增加時,模型所結合的曲線就變得更多。這就像統計學里面的抽樣定理,即我們從樣本參數出發估計總體參數,且希望構建出的估計量為總體參數的相合、無偏估計。
下面我們繪制了另外一張非線性目標函數曲線圖。我們發現對于給定的目標函數,在饋送了所有的觀察樣本后,它將搜尋到***值。即尋找令目標函數***的參數(arg max)。
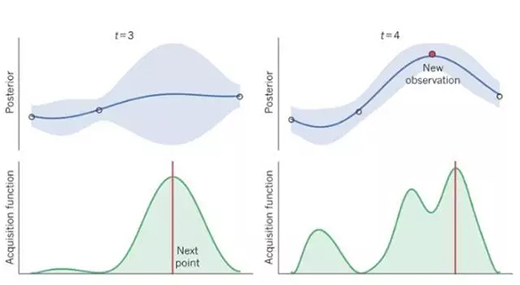
我們的目標并不是使用盡可能多的數據點完全推斷未知的目標函數,而是希望能求得***化目標函數值的參數。所以我們需要將注意力從確定的曲線上移開。當目標函數組合能提升曲線形成分布時,其就可以稱為采集函數(Acquisition funtion),這就是貝葉斯優化背后的思想。
因此,我們的目標首要就是確定令目標函數取***值的參數,其次再選擇下一個可能的***值,該***值可能就是在函數曲線上。
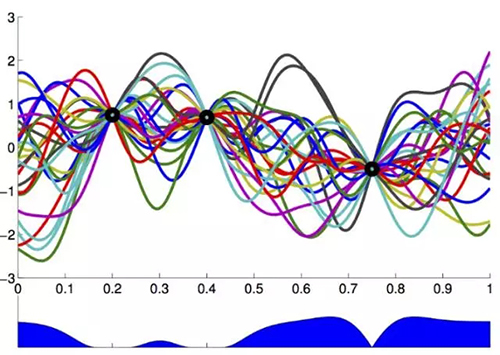
上圖是許多隨機集成曲線,它們都由三個黑色的觀察樣本所繪制而出。我們可以看到有許多波動曲線,它表示給定一個采樣點,下一個采樣點可能位于函數曲線的范圍。從下方的藍色區域可以看出,分布的方差是由函數曲線的均值得出。
因為我們疊加未知函數曲線的觀察值而進行估計,所以這是一種無噪聲的優化方法。但是當我們需要考慮噪聲優化方法時,我們未知的函數將會因為噪聲誤差值而輕微地偏離觀察樣本點。
貝葉斯優化的目標
我們一般希望能選取獲得***性能的超參數,因此超參數選擇就可以看作為一種***化問題,即***化超參數值為自變量的性能函數 f(x)。我們可以形式化為以下表達式:
許多優化設定都假設目標函數 f(x) 是已知的數學形式,同時還假定它為容易評估的凸函數。但是對于調參來說,目標函數是未知的,且它為計算昂貴的非凸函數。所以常用的優化方法很難起到作用,我們需要專門的貝葉斯優化方法來解決這一類問題。
貝葉斯優化方法在目標函數未知且計算復雜度高的情況下極其強大,該算法的基本思想是基于數據使用貝葉斯定理估計目標函數的后驗分布,然后再根據分布選擇下一個采樣的超參數組合。
貝葉斯優化充分利用了前一個采樣點的信息,其優化的工作方式是通過對目標函數形狀的學習,并找到使結果向全局***提升的參數。貝葉斯優化根據先驗分布,假設采集函數而學習到目標函數的形狀。在每一次使用新的采樣點來測試目標函數時,它使用該信息來更新目標函數的先驗分布。然后,算法測試由后驗分布給出的最值可能點。
高斯過程
為了使用貝葉斯優化,我們需要一種高效的方式來對目標函數的分布建模。這比直接對真實數字建模要簡單地多,因為我們只需要用一個置信的分布對 f(x) 建模就能求得***解。如果 x 包含連續型超參數,那么就會有無窮多個 x 來對 f(x) 建模,即對目標函數構建一個分布。對于這個問題,高斯過程(Gaussian Process)實際上生成了多維高斯分布,這種高維正態分布足夠靈活以對任何目標函數進行建模。
逼近目標函數的高斯過程
在上圖中,假定我們的目標函數(虛線)未知,該目標函數是模型性能和超參數之間的實際關系。但我們的目標僅僅是搜索令性能達到***的超參數組合。
開發和探索之間的權衡
一旦我們對目標函數建了模,那么我們就能抽取合適的樣本嘗試計算,這就涉及到了開發(exploitation)和探索(exploration)之間的權衡,即模型到底是在當前***解進一步開發,還是嘗試探索新的可能解。
對于貝葉斯優化,一旦它找到了局部***解,那么它就會在這個區域不斷采樣,所以貝葉斯優化很容易陷入局部***解。為了減輕這個問題,貝葉斯優化算法會在探測和開發 (exploration and exploitation) 中找到一個平衡點。
探測(exploration)就是在還未取樣的區域獲取采樣點。開發(exploitation)就是根據后驗分布,在最可能出現全局***解的區域進行采樣。我們下一個選取點(x)應該有比較大的均值(開發)和比較高的方差(探索)。
選擇下一個可能的***點,并在方差和均值間權衡。因為我們在高方差分布中搜索下一點,這意味著探測新的點 x。高均值意味著我們在較大偏移/偏差下選擇下一點(x)。
在給定前 t 個觀察樣本,我們可以利用高斯過程計算出觀察值的可能分布,即:
μ和σ的表達式如下,其中 K 和 k 是由正定核推導出的核矩陣和向量。具體來說,K_ij=k(x_i,x_j) 為 t 乘 t 階矩陣,k_i=k(x_i,x_t+1) 為 t 維向量。***,y 為觀察樣本值的 t 維向量。
上面的概率分布表明在擬合數據后,樣本點 x 的預測值 y 成高斯分布。并且該高斯分布有樣本均值和樣本方差這兩個統計量。現在為了權衡開發和探索,我們需要選擇下一點到底是均值較高(開發)還是方差較大(探索)。
采集函數
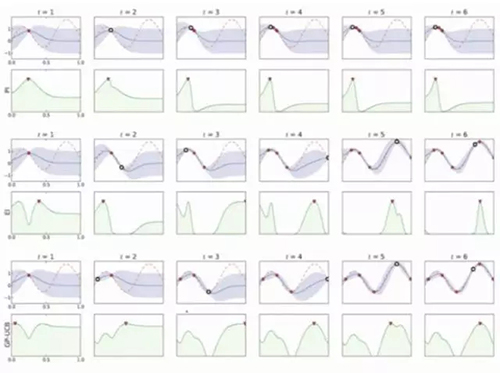
為了編碼開發探索之間的權衡,我們需要定義一個采集函數(Acquisition function)而度量給定下一個采樣點,到底它的效果是怎樣的。因此我們就可以反復計算采集函數的極大值而尋找下一個采樣點。
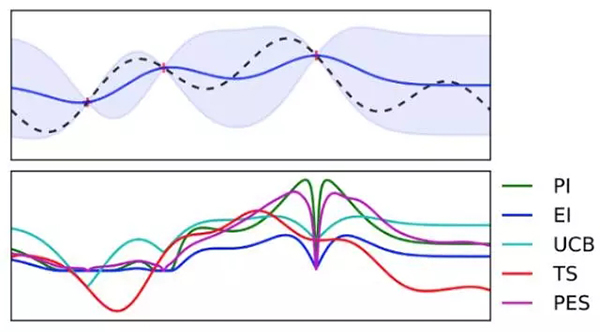
隨著樣本增加,不同的采集函數和曲線擬合的對比。
上置信邊界
也許最簡單的采集函數就是采取有較高期望的樣本點。給定參數 beta,它假設該樣本點的值為均值加上 beta 倍標準差,即:
通過不同的 beta 值,我們可以令算法傾向于開發還是探索。
提升的概率
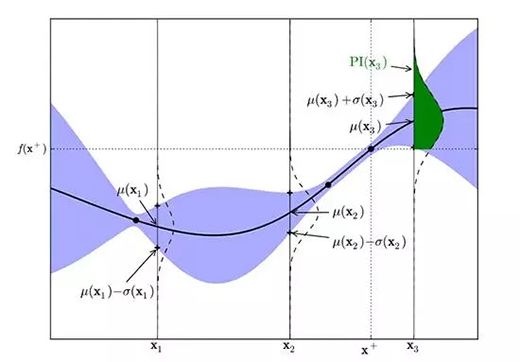
提升采集函數概率背后的思想,即我們在***化提升概率(MPI)的基礎上選擇下一個采樣點。
高斯過程的提升概率
在上圖中,***觀察值是在 x*上的 y*,綠色區域給出了在 x_3 點的提升概率,而 x_1 和 x_2 點的提升概率非常小。因此,在 x_3 點抽樣可能會在 y*的基礎上得到提升。
其中Φ(x) 為標準正態分布函數。
貝葉斯優化過程
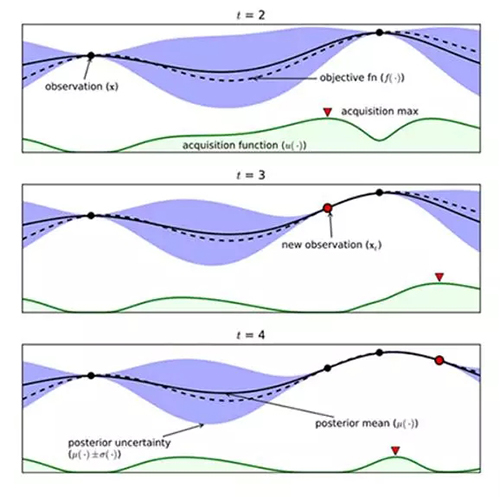
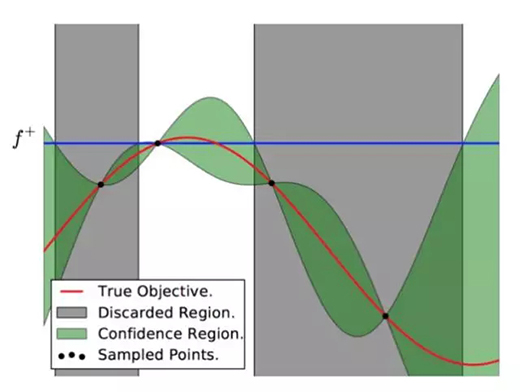
上圖可以直觀地解釋貝葉斯優化。其中紅色的曲線為實際的目標函數,并且我們并不知道該函數確切的表達式。所以我們希望使用高斯過程逼近該目標函數。通過采樣點(上圖有 4 個抽樣點),我們能夠得出直觀或置信曲線以擬合觀察到的樣本點。所以上圖綠色的區域為置信域,即目標曲線最有可能處于的區域。從上面的先驗知識中,我們確定了第二個點(f+)為***的樣本觀察值,所以下一個***點應該要比它大或至少與之相等。因此,我們繪制出一條藍線,并且下一個***點應該位于這一條藍線之上。因此,下一個采樣在交叉點 f+和置信域之間,我們能假定在 f+點以下的樣本是可以丟棄的,因為我們只需要搜索令目標函數取極大值的參數。所以現在我們就縮小了觀察區域,我們會迭代這一過程,直到搜索到***解。下圖是貝葉斯優化算法的偽代碼:
論文:Taking the Human Out of the Loop: A Review of Bayesian Optimization
地址:http://ieeexplore.ieee.org/document/7352306/
摘要:大數據應用通常和復雜系統聯系到一起,這些系統擁有巨量用戶、大量復雜性軟件系統和大規模異構計算與存儲架構。構建這樣的系統通常也面臨著分布式的設計選擇,因此最終產品(如推薦系統、藥物分析工具、實時游戲引擎和語音識別等)涉及到許多可調整的配置參數。這些參數通常很難由各種開發者或團隊具體地編入軟件中。如果我們能聯合優化這些超參數,那么系統的性能將得到極大的提升。貝葉斯優化是一種聯合優化超參數的強力工具,并且最近也變得越來越流行。它能自動調節超參數以提升產品質量和人類生產力。該綜述論文介紹了貝葉斯優化,并重點關注該算法的方法論和列舉一些廣泛應用的案例。
原文:
- https://cloud.google.com/blog/big-data/2017/08/hyperparameter-tuning-in-cloud-machine-learning-engine-using-bayesian-optimization
- https://medium.com/towards-data-science/shallow-understanding-on-bayesian-optimization-324b6c1f7083
【本文是51CTO專欄機構“機器之心”的原創譯文,微信公眾號“機器之心( id: almosthuman2014)”】