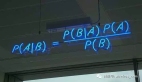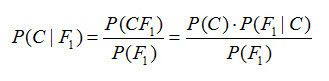譯者 | 朱先忠
審校 | 重樓
駕馭復雜性:預測醫(yī)療保健中的患者數(shù)量

在醫(yī)療保健領域,準確預測即將到來的患者數(shù)量不僅對手術成功至關重要,也是一個非常棘手的問題。原因很簡單:需要考慮的依賴性因素太多了——患者的嚴重程度和特殊要求、管理需求、檢查室限制、員工請病假、嚴重的暴風雪等等。更糟糕的是,意外情況可能會對日程安排和資源分配產生連鎖影響,甚至可能與最高質量的Excel項目預測結果產生矛盾。
從數(shù)據(jù)的角度來看,這些挑戰(zhàn)真的很有趣,因為它們極其復雜,足夠你考慮一段時間的。但是,即使是輕微的改進也可能帶來重大的勝利(例如,提高患者吞吐量、縮短等待時間、讓醫(yī)療保健提供者更快樂、降低成本等)。
另一種預測方法:貝葉斯模型
那么,還有什么替代方案呢?Epic為我們提供了大量數(shù)據(jù),包括患者何時赴約的實際記錄。在已知歷史“顯示”和“未顯示”的情況下,我們可以在監(jiān)督學習的空間中操作,貝葉斯網(wǎng)絡(BN:Bayesian Networks)提供了很好的概率圖形模型來預測未來的訪問概率。
雖然生活中的大多數(shù)決定都可以通過一個輸入來決定(例如,考慮“我應該帶雨衣嗎?”。假設外面下雨,那么這個決定應該是“是”),但貝葉斯網(wǎng)絡可以很容易地處理更復雜的決策——涉及多個輸入的決策(例如,天氣潮濕,步行僅3分鐘,你的雨衣在另一層樓,你的朋友可能有傘,等等),具有不同的概率結果和依賴性。在這篇文章中,我將在Python語言環(huán)境中構造一個超簡單的貝葉斯網(wǎng)絡,它可以根據(jù)癥狀、癌癥分期和治療目標這三個因素的已知概率,輸出患者在2個月內到達的概率得分。
理解貝葉斯網(wǎng)絡
貝葉斯網(wǎng)絡的核心是使用有向無環(huán)圖(DAG)的聯(lián)合概率分布的圖形表示。DAG中的節(jié)點表示隨機變量,有向邊表示這些變量之間的因果關系或條件依賴關系。正如所有數(shù)據(jù)科學項目一樣,在一開始就花大量時間與利益相關者協(xié)商,以正確映射決策中涉及的工作流程(例如變量),這對于高質量的預測結果是至關重要的。
因此,我將發(fā)明一個場景,讓我們與乳腺腫瘤合作伙伴會面,由他們來解釋三個變量——患者癥狀、癌癥分期和當前治療目標,對于確定患者是否需要在2個月內預約至關重要。
(事實上,影響未來患者數(shù)量的因素不下幾十個,其中一些是單一或多重依賴性的,另一些則是完全獨立但仍有影響的)。
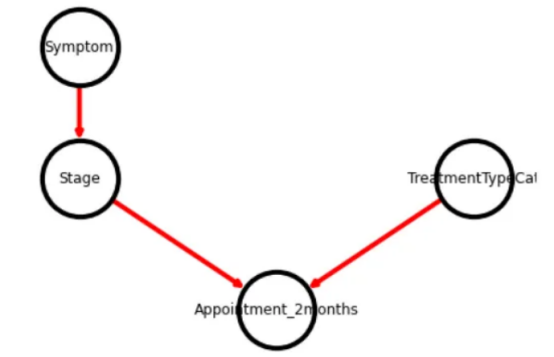
現(xiàn)在,假設我們同意如下工作流程:階段取決于他們的癥狀,但治療類型與癥狀無關,也影響到2個月內的預約。
基于此,我們將從我們的數(shù)據(jù)源(對我們來說是Epic)中獲取這些變量的數(shù)據(jù),該數(shù)據(jù)源將再次包含我們的分數(shù)節(jié)點(Appointment_2months)的已知值,標記為“是”或“否”。這種數(shù)據(jù)整理是一個重要部分;你需要根據(jù)這些變量在2個月前表明的情況,正確地捕捉2個月內真正到達患者的病例。
# 安裝包
import pandas as pd # 用于數(shù)據(jù)處理
import networkx as nx # 用于繪圖
import matplotlib.pyplot as plt # 用于繪圖
!pip install pybbn
# 用于創(chuàng)建貝葉斯置信網(wǎng)絡(BBN)
from pybbn.graph.dag import Bbn
from pybbn.graph.edge import Edge, EdgeType
from pybbn.graph.jointree import EvidenceBuilder
from pybbn.graph.node import BbnNode
from pybbn.graph.variable import Variable
from pybbn.pptc.inferencecontroller import InferenceController
# 通過手動鍵入概率創(chuàng)建節(jié)點
Symptom = BbnNode(Variable(0, 'Symptom', ['Non-Malignant', 'Malignant']), [0.30658, 0.69342])
Stage = BbnNode(Variable(1, 'Stage', ['Stage_III_IV', 'Stage_I_II']), [0.92827, 0.07173,
0.55760, 0.44240])
TreatmentTypeCat = BbnNode(Variable(2, 'TreatmentTypeCat', ['Adjuvant/Neoadjuvant', 'Treatment', 'Therapy']), [0.58660, 0.24040, 0.17300])
Appointment_2weeks = BbnNode(Variable(3, 'Appointment_2weeks', ['No', 'Yes']), [0.92314, 0.07686,
0.89072, 0.10928,
0.76008, 0.23992,
0.64250, 0.35750,
0.49168, 0.50832,
0.32182, 0.67818])上面代碼中,讓我們手動輸入每個變量(節(jié)點)中對應級別的一些概率值。注意,這些概率值沒有被猜測,甚至會是最好的猜測結果。不過,在實踐應用中,您還將再次根據(jù)現(xiàn)有數(shù)據(jù)來計算對應的頻率。
讓我們以癥狀(symptom)變量為例。我會得到它們的2級頻率值:大約31%是非惡性的,69%是惡性的,請參考下圖:
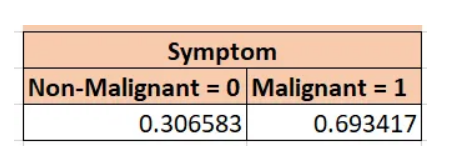
然后,我們考慮下一個變量Stage,并使用Symptom進行交叉表計算,以獲得這些頻率。我們這樣做是因為階段(Stage)取決于癥狀(Symptom),因為它們每個變量都對應兩個場景,所以它們實際上存在4個概率結果。
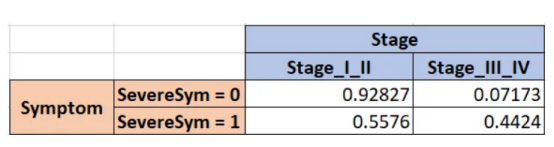
依此類推,直到定義了父子對之間的所有交叉表。
現(xiàn)在,大多數(shù)貝葉斯網(wǎng)絡包括許多父子關系,因此計算概率可能會變得乏味(而且非常容易出錯),下面的函數(shù)可以用來計算與0、1或2個父節(jié)點對應的任何子節(jié)點的概率矩陣。雖然醫(yī)學洞見不能也不應該被自動化處理,但數(shù)據(jù)準備部分的工作完全可以也應該通過自動化的方式來實現(xiàn)。
# 此函數(shù)有助于計算進入BBN的概率分布(注意,最多可以處理2個父節(jié)點)
def probs(data, child, parent1=None, parent2=None):
if parent1==None:
# 計算概率
prob=pd.crosstab(data[child], 'Empty', margins=False, normalize='columns').sort_index().to_numpy().reshape(-1).tolist()
elif parent1!=None:
# 檢查子節(jié)點是否有1個父節(jié)點或2個父節(jié)點
if parent2==None:
# 計算概率
prob=pd.crosstab(data[parent1],data[child], margins=False, normalize='index').sort_index().to_numpy().reshape(-1).tolist()
else:
# 計算概率
prob=pd.crosstab([data[parent1],data[parent2]],data[child], margins=False, normalize='index').sort_index().to_numpy().reshape(-1).tolist()
else: print("Error in Probability Frequency Calculations")
return prob接下來,我們創(chuàng)建實際的貝葉斯網(wǎng)絡節(jié)點和網(wǎng)絡本身:
# 通過使用我們早期的函數(shù)自動計算概率來創(chuàng)建節(jié)點
Symptom = BbnNode(Variable(0, 'Symptom', ['Non-Malignant', 'Malignant']), probs(df, child='SymptomCat'))
Stage = BbnNode(Variable(1, 'Stage', ['Stage_I_II', 'Stage_III_IV']), probs(df, child='StagingCat', parent1='SymptomCat'))
TreatmentTypeCat = BbnNode(Variable(2, 'TreatmentTypeCat', ['Adjuvant/Neoadjuvant', 'Treatment', 'Therapy']), probs(df, child='TreatmentTypeCat'))
Appointment_2months = BbnNode(Variable(3, 'Appointment_2months', ['No', 'Yes']), probs(df, child='Appointment_2months', parent1='StagingCat', parent2='TreatmentTypeCat'))
# 創(chuàng)建貝葉斯網(wǎng)絡
bbn = Bbn() \
.add_node(Symptom) \
.add_node(Stage) \
.add_node(TreatmentTypeCat) \
.add_node(Appointment_2months) \
.add_edge(Edge(Symptom, Stage, EdgeType.DIRECTED)) \
.add_edge(Edge(Stage, Appointment_2months, EdgeType.DIRECTED)) \
.add_edge(Edge(TreatmentTypeCat, Appointment_2months, EdgeType.DIRECTED))
# 將BBN轉換為連接樹
join_tree = InferenceController.apply(bbn)現(xiàn)在,我們準備好了一切。接下來,讓我們通過貝葉斯網(wǎng)絡運行一些假設,并給出評估輸出。
評估貝葉斯網(wǎng)絡輸出
首先,讓我們看看每個節(jié)點的概率,而不需要具體聲明任何條件。
# 定義打印邊際概率的函數(shù)
#每個節(jié)點的概率
def print_probs():
for node in join_tree.get_bbn_nodes():
potential = join_tree.get_bbn_potential(node)
print("Node:", node)
print("Values:")
print(potential)
print('----------------')
# 使用以上函數(shù)打印邊際概率
print_probs()
輸出結果如下:
Node: 1|Stage|Stage_I_II,Stage_III_IV
Values:
1=Stage_I_II|0.67124
1=Stage_III_IV|0.32876
----------------
Node: 0|Symptom|Non-Malignant,Malignant
Values:
0=Non-Malignant|0.69342
0=Malignant|0.30658
----------------
Node: 2|TreatmentTypeCat|Adjuvant/Neoadjuvant,Treatment,Therapy
Values:
2=Adjuvant/Neoadjuvant|0.58660
2=Treatment|0.17300
2=Therapy|0.24040
----------------
Node: 3|Appointment_2weeks|No,Yes
Values:
3=No|0.77655
3=Yes|0.22345
----------------上述情況表明,該數(shù)據(jù)集中的所有患者都有67%的概率為Stage_I_II,69%的概率為非惡性(Non-Malignant),58%的概率需要輔助/新輔助(Adjuvant/Neoadjuvant)治療,其中只有22%的患者需要在2個月后預約。
顯然,我們可以很容易地從沒有貝葉斯網(wǎng)絡的簡單頻率表中得到這一點。
但現(xiàn)在,讓我們問一個更有條件的問題:考慮到患者患有階段=Stage_I_II和TreatmentTypeCat=Therapy,患者在2個月內需要護理的可能性有多大。此外,考慮到醫(yī)療保健提供者對他們的癥狀一無所知(也許他們還沒有見過病人)。
我們將在節(jié)點中運行我們所知道的正確內容:
# 添加已發(fā)生事件的證據(jù),以便重新計算概率分布
def evidence(ev, nod, cat, val):
ev = EvidenceBuilder() \
.with_node(join_tree.get_bbn_node_by_name(nod)) \
.with_evidence(cat, val) \
.build()
join_tree.set_observation(ev)
# 添加更多證據(jù)
evidence('ev1', 'Stage', 'Stage_I_II', 1.0)
evidence('ev2', 'TreatmentTypeCat', 'Therapy', 1.0)
# 打印邊際概率
print_probs()上述代碼的執(zhí)行將返回如下內容:
Node: 1|Stage|Stage_I_II,Stage_III_IV
Values:
1=Stage_I_II|1.00000
1=Stage_III_IV|0.00000
----------------
Node: 0|Symptom|Non-Malignant,Malignant
Values:
0=Non-Malignant|0.57602
0=Malignant|0.42398
----------------
Node: 2|TreatmentTypeCat|Adjuvant/Neoadjuvant,Treatment,Therapy
Values:
2=Adjuvant/Neoadjuvant|0.00000
2=Treatment|0.00000
2=Therapy|1.00000
----------------
Node: 3|Appointment_2months|No,Yes
Values:
3=No|0.89072
3=Yes|0.10928
----------------上面結果顯示,這個病人在兩個月內到達的幾率只有11%。我們可以詢問我們變量的已知或未知特征的任何排列,以預測患者在2個月內到達的概率。可以利用進一步的算法和函數(shù)來收集許多患者或患者組的概率,或優(yōu)化這些概率。
關于質量輸入變量重要性的說明
Python代碼編寫是一回事,但貝葉斯網(wǎng)絡在提供可靠的未來就診估計方面的真正成功在很大程度上取決于患者護理工作流程的準確映射。所有這些需要時間、談話和白板——而不是僅僅的編碼工作。這樣的信息取得甚至可能需要幾次數(shù)據(jù)挖掘,并與客戶重新接觸,以進行壓力測試假設:“我們之前說過,護士導航儀總是在報告癥狀不佳后給患者打電話,但這種情況只發(fā)生了10%。下一次與患者交談是與他們的醫(yī)療服務提供者進行的。”。
在類似的情況下,表現(xiàn)相似的患者通常需要類似的服務,并以類似的節(jié)奏進入。這些輸入的排列,其特征可以從臨床到管理,最終對應于服務需求的某種確定性路徑。但是,時間預測越復雜或越遠,就越需要更具體、更復雜的具有高質量輸入的貝葉斯網(wǎng)絡。
原因如下:
- 精確表示:貝葉斯網(wǎng)絡的結構必須反映變量之間的實際關系。選擇不當?shù)淖兞炕蛘`解的依賴關系可能導致不準確的預測和見解。
- 有效推理:高質量的輸入變量增強了模型執(zhí)行概率推理的能力。當變量根據(jù)其條件依賴性準確連接時,網(wǎng)絡可以提供更可靠的見解。
- 降低復雜性:包含不相關或冗余的變量會使模型不必要地復雜化,并增加計算需求。高質量的投入使網(wǎng)絡更加高效。
譯者介紹
朱先忠,51CTO社區(qū)編輯,51CTO專家博客、講師,濰坊一所高校計算機教師,自由編程界老兵一枚。
原文標題:Using Bayesian Networks to forecast ancillary service volume in hospitals,作者:Gabe Verzino