本文經AI新媒體量子位（公眾號ID:QbitAI）授權轉載，轉載請聯系出處。

快排堆排冒泡排。排序，在計算機中是再常見不過的算法。

在機器學習中，排序也經常用于統計數據、信息檢索等領域。

那么問題來了，排序算法在函數角度上是分段線性的，也就是說，在幾個分段的“節點”處是不可微的。這樣，就給反向傳播造成了困難。

現在，谷歌大腦針對這一問題，提出了一種快速可微分排序算法，并且，時間復雜度達到了O(nlogn)，空間復雜度達為O(n)。

速度比現有方法快出一個數量級！

代碼的PyTorch、TensorFlow和JAX版本即將開源。

快速可微分排序算法

現代深度學習架構通常是通過組合參數化功能塊來構建，并使用梯度反向傳播進行端到端的訓練。

這也就激發了像LeCun提出的可微分編程 (differentiable programming)的概念。

雖然在經驗上取得了較大的成功，但是許多操作仍舊存在不可微分的問題，這就限制了可以計算梯度的體系結構集。

諸如此類的操作就包括排序 (sorting)和排名 (ranking)。

從函數角度來看都是分段線性函數，排序的問題在于，它的向量包含許多不可微分的“節點”，而排名的秩要比排序還要麻煩。

首先將排序和排名操作轉換為在排列多面體(permutahedron)上的線性過程，如下圖所示。

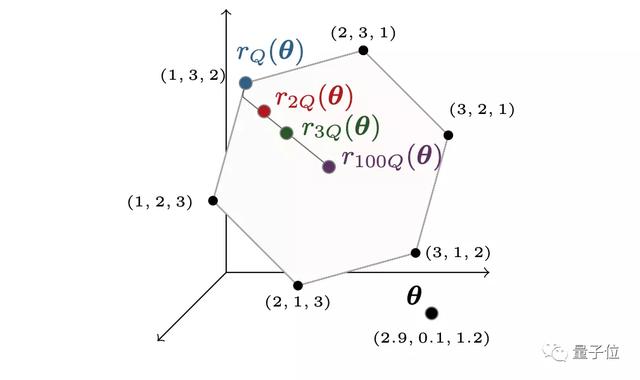
△排列多面體說明

在這一過程后，可以發現對于r(θ)，若是θ出現微小“擾動”，就會導致線性程序跳轉到另外一個排序，使得r(θ)不連續。

也就意味著導數要么為null，要么就是“未定義”，這就阻礙了梯度反向傳播。

為了解決上述的問題，就需要對排序和排名運算符，進行有效可計算的近似設計。

谷歌大腦團隊提出的方法，就是通過在線性規劃公式中引入強凸正則化來實現這一目標。

這就讓它們轉換成高效可計算的投影算子(projection operator)，可微分，且服從于形式分析(formal analysis)。

在投影到排列多面體之后，可以根據這些投影來定義軟排序(soft sorting)和軟排名(soft ranking)操作符。

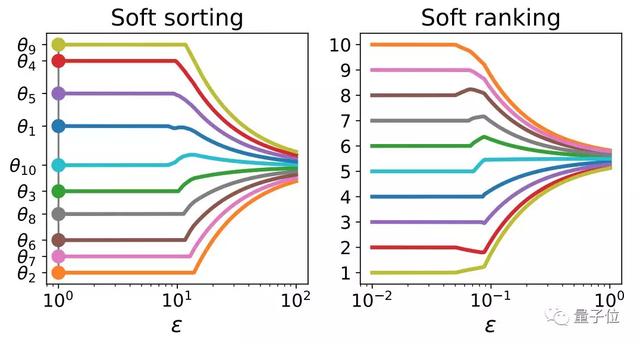
△軟排序和軟排名操作符

在此基礎上，要想完成快速計算和微分，一個關鍵步驟就是將投影簡化為保序優化 (isotonic optimization)。

接下來是將保序優化進行微分，此處采用的是雅可比矩陣(Jacobian)，因為它簡單的塊級結構，使得導數很容易分析。

而后，結合命題3和引理2，可以描述投影到排列多面體上的雅可比矩陣。

需要強調的是，與保序優化的雅可比矩陣不同，投影的雅可比矩陣不是塊對角的，因為我們需要對它的行和列進行轉置。

最終，可以用O(n)時間和空間中的軟算子雅可比矩陣相乘。

實驗結果

研究人員在CIFAR-10和CIFAR-100數據集上進行了實驗。

實驗使用的CNN，包含4個具有2個最大池化層的Conv2D，RelU激活，2個完全連接層；ADAM優化器的步長恒定為10-4，k=1。

與之比較的是O(Tn2)的OT方法，以及O(n2)的All-pairs方法。

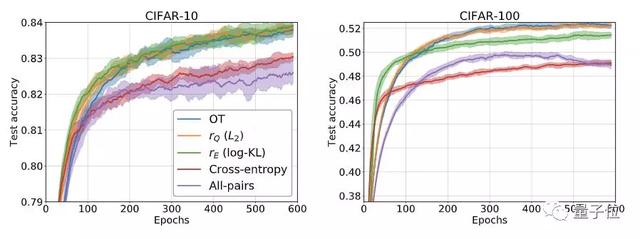
△rQ及rE為新算法

結果表明，在CIFAR-10和CIFAR-100上，新算法都達到了與OT方法相當的精度，并且速度明顯更快。

在CIFAR-100上訓練600個epoch，OT耗費的時間為29小時，rQ為21小時，rE為23小時，All-pairs為16小時。在CIFAR-10上結果差不多。

在驗證輸入尺寸對運行時間的影響時，研究人員使用的是64GB RAM的6核Intel Xeon W-2135，以及GeForce GTX 1080Ti。

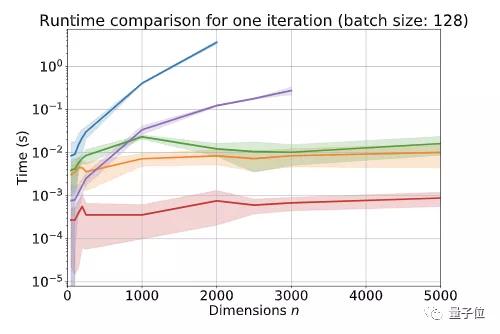
禁用反向傳播的情況下，進行1個batch的計算，OT和All-pairs分別在n=2000和n=3000的時候出現內存不足。

啟用反向傳播時，OT和All-pairs分別在n=1000和n=2500的時候出現內存不足。

開啟新的可能性

曾就職于谷歌、NASA的機器學習工程師Brad Neuberg認為，從機器學習的角度來說，快速可微分排序、排名算法看上去十分重要。

而谷歌的這一新排序算法，也在reddit和hacker news等平臺上引起了熱烈的討論。

有網友對其帶來的“新可能性”做出了更為詳細的討論：

我想，可微分排序生成的梯度信息量更大，使得梯度下降的速度更快，從而能夠進一步提升訓練速度。

我認為，這意味著某些基于排名的指標，以后可以用可微分的形式來表示。也就是說，神經網絡可以輕松地針對這些結果直接進行優化。

對于谷歌而言，這很顯然會應用于網絡搜索，以及諸如標簽分配之類的東西問題。

也有網友指出，雖然該算法并不是第一個解決了排序不可微問題的方法，但它的效率無疑更高。

傳送門

論文：https://arxiv.org/pdf/2002.08871.pdf

討論：https://news.ycombinator.com/item?id=22393790https://www.reddit.com/r/MachineLearning/comments/f85yp4/r_fast_differentiable_sorting_and_ranking/