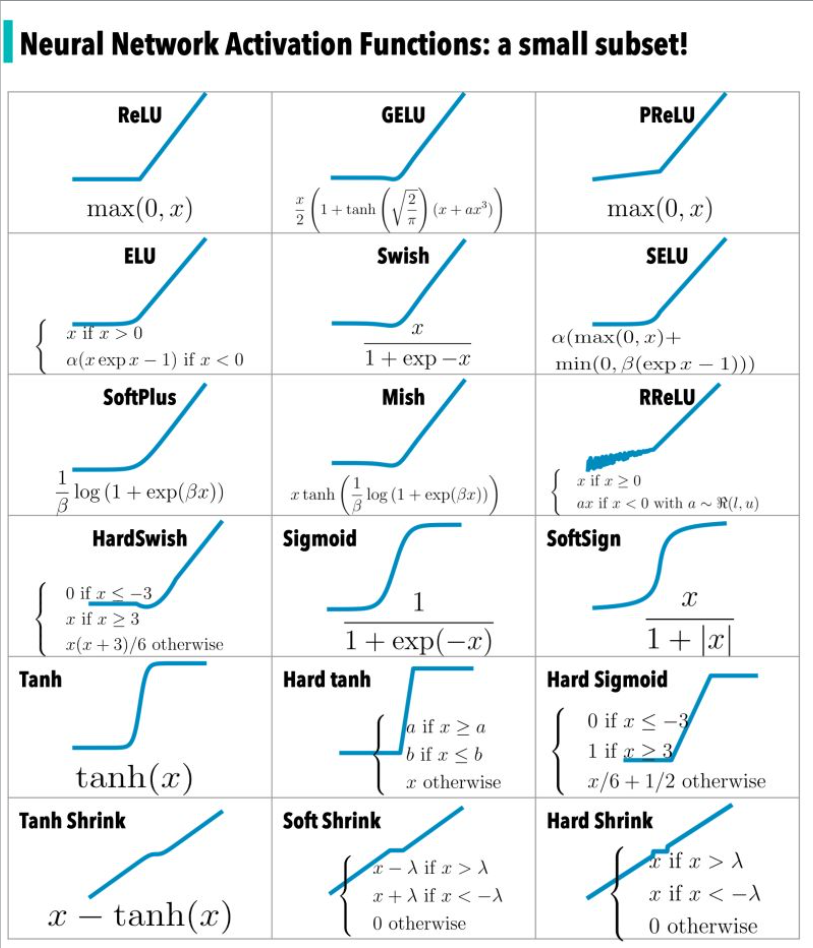
在《神經網絡中常見的激活函數》一文中對激活函數進行了回顧，下圖是激活函數的一個子集——

而在神經網絡領域中的另一類重要的函數就是損失函數，那么，什么是損失函數呢？

損失函數是將隨機事件或其有關隨機變量的取值映射為非負實數以表示該隨機事件的“風險”或“損失”的函數，用于衡量預測值與實際值的偏離程度。在機器學習中，損失函數是代價函數的一部分，而代價函數是目標函數的一種類型。在應用中，損失函數通常作為學習準則與優化問題相聯系，即通過最小化損失函數求解和評估模型。

這里簡要回顧一些常見的損失函數及其簡明用例。為了便于理解，將損失函數分為兩類：面向分類的損失函數和面向回歸的損失函數。 為了便于不同損失函數的比較，常將其表示為單變量的函數，在回歸問題中這個變量為y?f(x)，在分類問題中則為yf(x)。

面向分類的損失函數

對于二分類問題，y∈{?1,+1}，損失函數常表示為關于yf(x)的單調遞減形式。yf(x)被稱為margin，最小化損失函數也可以看作是最大化 margin 的過程，任何合格的分類損失函數都應該對 margin<0 的樣本施以較大的懲罰。

Cross Entropy Loss 損失函數

物理學上的熵表示一個熱力學系統的無序程度。為了解決對信息的量化度量問題，香農在1948年提出了“信息熵”的概念，使用對數函數表示對不確定性的測量。熵越高，表示能傳輸的信息越多，熵越少，表示傳輸的信息越少，可以直接將熵理解為信息量。

交叉熵(cross-entropy，CE)刻畫了兩個概率分布之間的距離，更適合用在分類問題上，因為交叉熵表達預測輸入樣本屬于某一類的概率。

Cross Entropy loss損失函數，或負對數損失，衡量輸出為0到1之間的概率值的分類模型的性能，常用于二分類和多分類問題中。交叉熵損失隨著預測的概率值遠離實際標簽而增加。一個完美的模型將會是0損失，因為預測的值將會匹配實際的值。

對二分類，交叉熵損失的公式如下：

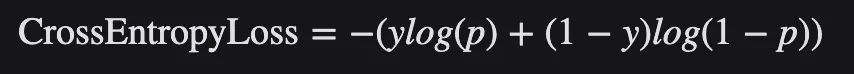
在多分類任務中，經常采用 softmax 激活函數+交叉熵損失函數，因為交叉熵描述了兩個概率分布的差異，然而神經網絡輸出的是向量，并不是概率分布的形式。所以需要 softmax激活函數將一個向量進行“歸一化”成概率分布的形式，再采用交叉熵損失函數計算 loss。

對于多分類，交叉熵損失的公式如下：

Focal Loss 損失函數

Focal loss 損失函數是為了解決 one-stage 目標檢測中正負樣本極度不平衡的問題，是一個密集目標檢測的損失函數。在訓練深層神經網絡解決目標檢測和分類問題時，這是最常見的選擇之一。

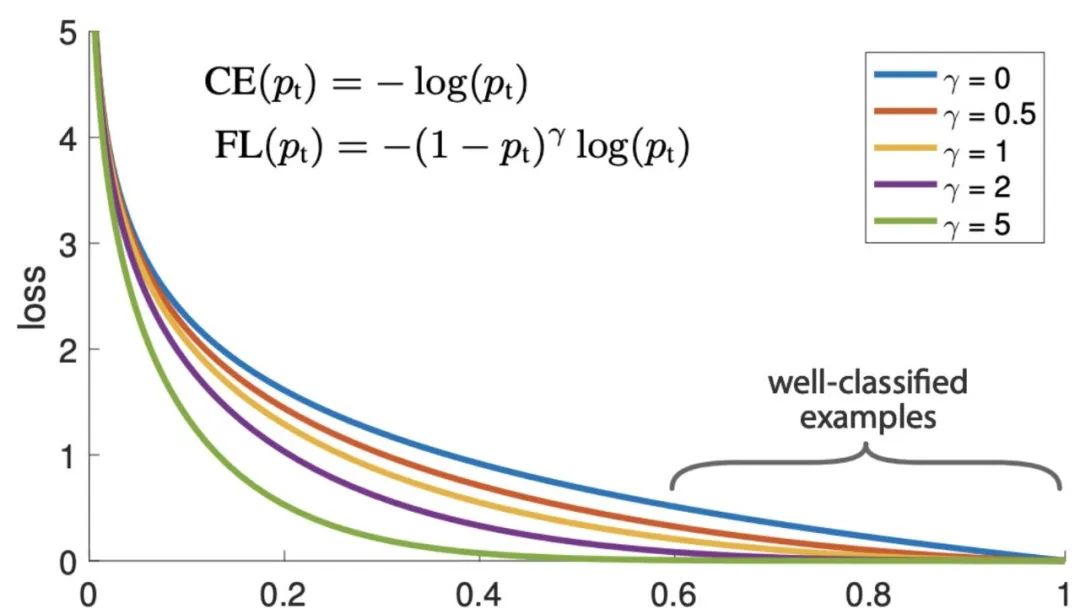
Focal loss損失函數是基于二分類交叉熵的，通過一個動態縮放因子，可以動態降低訓練過程中易區分樣本的權重，從而將重心快速聚焦在那些難區分的樣本。那些樣本有可能是正樣本，也有可能是負樣本，但都是對訓練網絡有幫助的樣本。

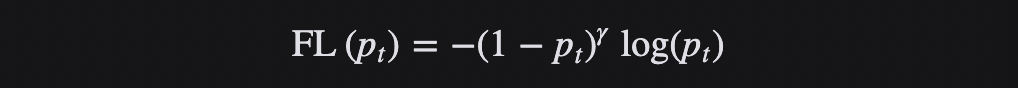
Focal loss損失函數計算一個動態縮放的交叉熵損失，如果其中的比例因子衰減為零，作為正確的類的置信度增加。

Polyloss 損失函數

Cross-entropy loss損失函數和 focal loss損失函數是深層神經網絡分類問題訓練中最常用的選擇。然而，一般來說，一個好的損失函數可以采取更加靈活的形式，應該為不同的任務和數據集量身定制。

可以將損失函數視為多項式函數的線性組合，并通過泰勒展開來近似函數。在多項式展開下，Focal Loss是多項式系數相對于Cross-entropy loss的水平位移。如果垂直修改多項式系數，則得到了Polyloss的計算公式：

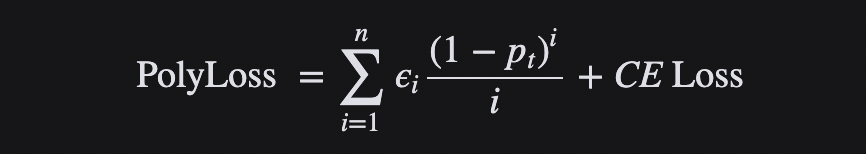
Polyloss是Cross-entropy loss損失函數的一種廣義形式。

Hinge Loss 損失函數

Hinge loss損失函數通常適用于二分類的場景中，可以用來解決間隔最大化的問題，常應用于著名的SVM算法中。

Hinge 損失函數是一個凸函數，擅長“最大余量”分類，因此許多機器學習中常用的凸優化器都可以利用它。

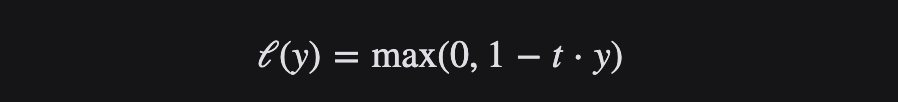
Hinge 損失函數將與分類邊界之間的差值或距離納入成本計算。即使新的觀察結果被正確分類，如果決策邊界的差距不夠大，它們也會受到懲罰，損失呈線性增加。

Generalized End-to-End Loss 損失函數

Generalized End-to-End 損失函數（簡稱GE2E）用于說話人驗證的廣義端到端損失函數。

說話人驗證是指驗證輸入的一段語音是否屬于一個特定音箱的任務，這里有兩個概念：enrollment utterance和verification utterance，前者可以理解為預留的“聲紋”，而后者則是用于驗證的語音。進一步細分為兩種任務：text-dependent speaker verification (TD-SV)和text-independent verification (TI-SV)。TD-SV對用于驗證的語音的內容有一定的限制，一個比較常見的例子是Siri，這個時候需要說出一個固定的句子“Hey, siri”。相反，TI-SV則不對語音的內容有任何限制。

GE2E 使說話人驗證模型的訓練比tuple-based end-to-end (TE2E) loss 損失函數更有效率，具有收斂速度快、實現簡單等優點。

GE2E會使得網絡在更新參數的時候注重于那些不容易被區分開的數據，且不需要在訓練之前進行示例選擇。此外，GE2E Loss不需要初始階段的示例選擇。

Additive Angular Margin Loss 損失函數

Additive Angular Margin Loss（AAM）主要用于人臉識別，但也在語音識別等其他領域得到了應用。

利用深層卷積神經網絡(DCNN)進行大規模人臉識別的特征學習面臨的主要挑戰之一是如何設計合適的損失函數來提高識別能力。中心損失懲罰了深部特征與其在歐氏空間中相應的類中心之間的距離，以實現類內緊湊性。假設最后一個完全連通層中的線性映射矩陣可以用來表示角度空間中的類中心，并以乘法的方式懲罰深層特征及其相應權重之間的角度。一個流行的研究方向是將預留邊緣納入已建立的損失函數，以最大限度地提高人臉的可分性。

AAM Loss(ArcFace)由于與超球面上的測地距離精確對應，獲得了具有清晰幾何解釋(優于其他損失函數)的高度區分特征。ArcFace 的性能始終優于最先進的技術，并且可以輕松實現，計算開銷可以忽略不計。

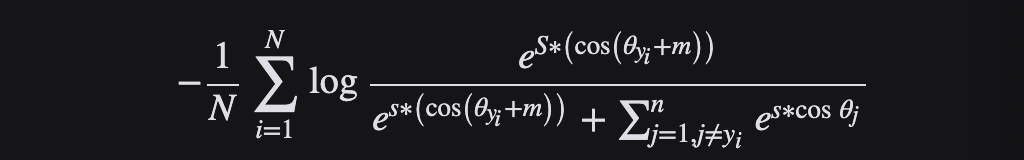
具體來說，提出的弧面 cos (θ + m)基于 L2歸一化權重和特征，直接最大化角(弧)空間的決策邊界。

Triplet Loss 損失函數

Triplet Loss最初用于學習同一人在不同姿勢和角度下的人臉識別。Triplet Loss是機器學習算法的一種損失函數，其中一個參考輸入(稱為錨)與一個匹配輸入(稱為正值)和一個非匹配輸入(稱為負值)進行比較。

考慮訓練神經網絡識別人臉的任務(例如進入高安全區域)。每當一個新的人加入到人臉數據庫時，訓練有素的分類器就必須重新訓練。這可以通過將問題作為一個相似性學習問題而不是一個分類問題來避免。這里，網絡被訓練(使用對比度損失)輸出一個距離，如果圖像屬于一個已知的人，這個距離是小的，如果圖像屬于一個未知的人，這個距離是大的。但是，如果我們想輸出最接近給定圖像的圖像，我們希望了解一個排名，而不僅僅是相似性。在這種情況下使用了三重損失。

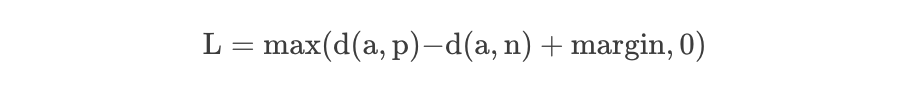
其中d 表示距離函數，一般指在Embedding下的歐式距離計算。很顯然，Triplet-Loss是希望讓a和p的距離盡可能小，而a和n的距離盡可能大。

在訓練中使用Triplet loss的一個重要選擇就是我們需要對負樣本進行挑選，稱之為負樣本選擇或者三元組采集。選擇的策略會對訓練效率和最終性能結果有著重要的影響。一個明顯的策略就是：簡單的三元組應該盡可能被避免采樣到，因為其loss為0，對優化并沒有任何幫助。

InfoNCE Loss 損失函數

InfoNCE Loss損失函數是基于對比度的一個損失函數，是由NCE Loss損失函數演變而來的。

NCE是基于采樣的方法，將多分類問題轉為二分類問題。以語言模型為例，利用NCE可將從詞表中預測某個詞的多分類問題，轉為從噪音詞中區分出目標詞的二分類問題，一個類是數據類別 data sample，另一個類是噪聲類別 noisy sample，通過學習數據樣本和噪聲樣本之間的區別，將數據樣本去和噪聲樣本做對比，也就是“噪聲對比（noise contrastive）”，從而發現數據中的一些特性。

Info NCE loss是NCE的一個簡單變體，它認為如果你只把問題看作是一個二分類，只有數據樣本和噪聲樣本的話，可能對模型學習不友好，因為很多噪聲樣本可能本就不是一個類，因此還是把它看成一個多分類問題比較合理。

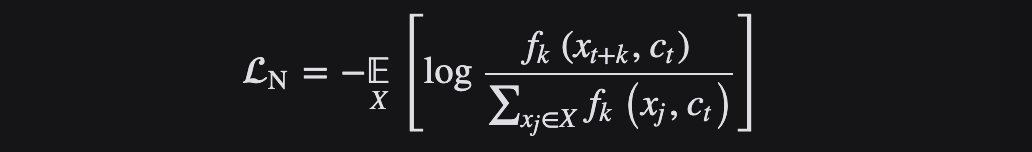
InfoNCE 代表噪聲對比估計，是一種用于自我監督學習的對比損失函數，使用分類交叉熵損失來識別一組不相關的噪聲樣本中的正樣本。InfoNCE Loss是為了將N個樣本分到K個類中，而不是NCE Loss的二分類或者交叉熵損失函數的完全分類。

Dice Loss 損失函數

Dice 損失函數來源于 S?rensen-Dice系數，這是一個發展于1940年代的統計方法，用來衡量兩個樣本之間的相似性。Dice系數的值越大意味著這兩個樣本越相似。

Dice Loss常用于語義分割問題中，對于二分類分割問題，真實分割標簽只有0，1兩個值。對于多分類分割問題，Dice Loss是直接優化F1 score而來的，是對F1 score的高度抽象。

2016年，Milletari 等人將其引入計算機視覺社區，用于三維醫療圖像分割。為了防止分母項為0，一般我們會在分子和分母處同時加入一個很小的數作為平滑系數，也稱為拉普拉斯平滑項。Dice Loss有以下主要特性：

• 有益于正負樣本不均衡的情況，側重于對前景的挖掘；
• 訓練過程中，在有較多小目標的情況下容易出現振蕩；
• 極端情況下會出現梯度飽和的情況。

從集合論的角度來看，DSC是兩個集合之間重疊的度量。例如，如果兩個集合 A 和 B 完全重疊，Dice系數 的最大值為1。否則，Dice系數開始減小，如果兩個集合完全不重疊，則 Dice系數的最小值為0。

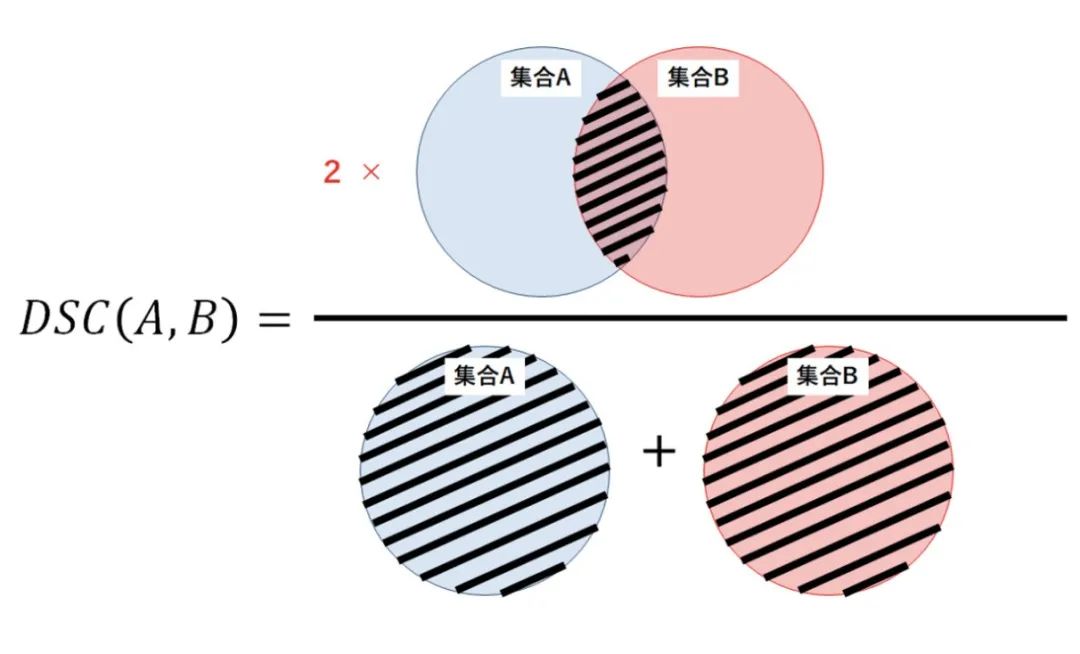
因此，DSC 的范圍在0-1之間，越大越好。因此，我們可以使用1-DSC 作為骰子損失，以最大限度地提高兩個集之間的重疊。

Margin Ranking Loss 損失函數

顧名思義，Margin Ranking Loss損失函數主要用于排名問題，也應用于對抗網絡中。Margin Ranking Loss計算輸入為 X1、 X2以及包含1或 -1的標簽張量 y 的損失。當 y 的值為1時，第一個輸入將被假設為較大的值，并將排名高于第二個輸入。類似地，如果 y =-1，第二個輸入將被排序得更高。

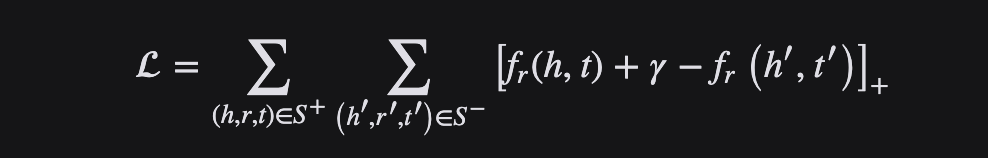
Margin Ranking Loss 計算一個標準來預測輸入之間的相對距離。這不同于其他損失函數，例如 MSE 或交叉熵，它們學習直接從一組給定的輸入進行預測。

Contrastive Loss 損失函數

鑒于學習不變映射的降維需求，對比損失是一個交叉熵的替代損失函數，它可以更有效地利用標簽信息。

在孿生神經網絡（siamese network）中，其采用的損失函數是contrastive loss，這種損失函數可以有效的處理孿生神經網絡中的paired data的關系，形式上并不一定是兩個Net，也可以是一個Net兩個Out。

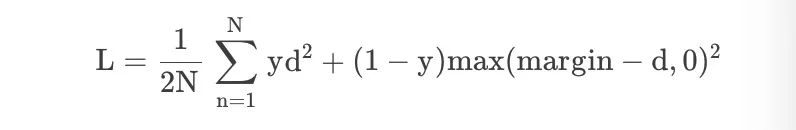
在嵌入空間中，同一類的點簇被拉在一起，同時推開不同類的樣本簇。Contrastive以網絡的輸出為正樣本，計算網絡到同類實例的距離，并與網絡到負類實例的距離進行對比。對比損失計算正例(同類的例子)和負例(不同類的例子)之間的距離。因此，如果正面例子被編碼(在這個嵌入空間中)到相似的例子中，而負面例子被進一步編碼到不同的表示中，那么損失可以預期是低的。

Multiple Negative Ranking Loss 損失函數

句表示領域中的核心其實是隱性的規定負例，例如只有錨定語句和一個正例，同一批次中的其他語句則為負例，或者指定一組錨定語句、正例、困難負例，同一批次的其他語句皆為負例等，使用的損失函數主要是Multiple Negative Ranking Loss，數學上的表達式為：

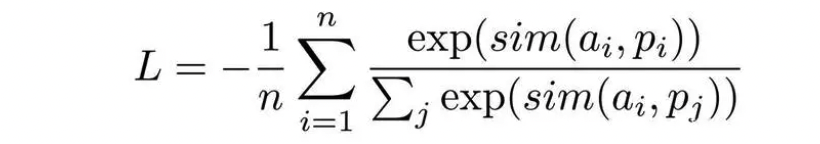
這個丟失函數可以很好地訓練嵌入，以便在檢索設置中使用正對(例如 query，relevant _ doc) ，因為它將在每批 n-1負文檔中隨機抽樣。性能通常隨著批量的增加而提高。

在高效句子嵌入問題中，使用Multiple Negative Ranking Loss 損失函數訓練的模型具有一定的優勢。

面向回歸的損失函數

回歸問題中y和f(x)皆為實數∈R，因此用殘差 y?f(x)來度量二者的不一致程度。殘差 (的絕對值) 越大，則損失函數越大，學習出來的模型效果就越差（這里不考慮正則化問題）。

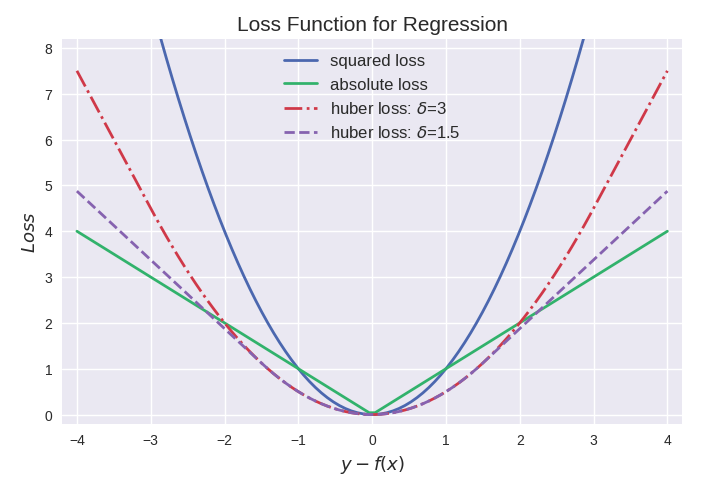
MAE 或 L1 Loss 損失函數

顧名思義，平均絕對誤差（Mean Average Error，MAE） 取實際值和預測值之間絕對差的平均和，也叫做“L1 損失函數”。它在一組預測中衡量誤差的平均大小，而不考慮誤差的方向。如果也考慮方向，那將被稱為平均偏差（Mean Bias Error,MBE），它是殘差或誤差之和，其損失范圍也是0到∞。

由于存在異常值(與其他數據非常不同的值) ，回歸問題可能有本質上不是嚴格高斯的變量。在這種情況下，平均絕對誤差將是一個理想的選擇，因為它沒有考慮到異常值的方向(不切實際的高正值或負值)。

L1損失函數用于最小化誤差，是以絕對誤差作為距離。L1不受離群值的影響，因此，如果數據集包含離群值，則 L1更可取。另外，其收斂速度快，能夠對梯度給予合適的懲罰權重，而不是“一視同仁”，使梯度更新的方向可以更加精確。

MSE 或 L2 Loss 損失函數

均方差（Mean Squared Error，MSE）是實際值和預測值之間的平方差的平均值，是最常用的回歸損失函數，也叫做“L2 損失函數”。MSE是目標變量與預測值之間距離平方之和。

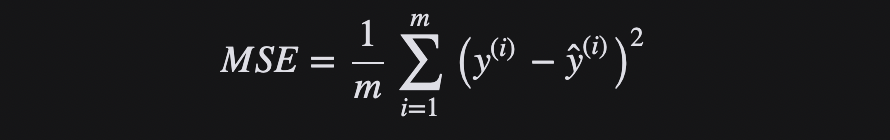
L2損失函數用來最小化誤差，也是比 L1更優先的損失函數。但是，當數據集中存在異常值時，L2的性能不會很好，因為平方差會導致更大的錯誤。

簡而言之，使用L2更容易求解，但使用L1對離群點更加魯棒。

Huber Loss 損失函數

Huber Loss 是一種將 MSE 與 MAE 結合起來，取兩者優點的損失函數，也被稱作 Smooth Mean Absolute Error Loss（Smooth L1 損失）。Huber Loss 也是回歸中使用的一種損失函數，它對數據中的異常值不如誤差平方損失那么敏感。它具有對異常點不敏感和極小可微的特點，使得損失函數具有良好的性質。

當誤差較小時，利用 Huber Loss的 MSE 部分，當誤差較大時，利用 Huber 損失的 MAE 部分。引入了一種新的超參數 δ，它告訴損失函數從 MSE 到 MAE 的切換位置。在損失函數中引入 δ 項，使 MSE 向 MAE 的轉變趨于平滑。Huber 損失函數描述了由估算過程產生的損失 F Huber 損失分段定義損失函數:

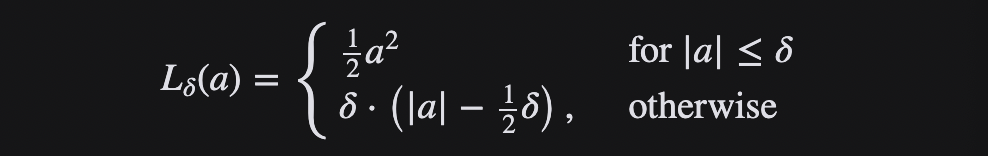
這個函數是二次函數，具有相等的值和斜率的不同部分在兩個點 ‖ a ‖ = δ 變量 a 通常指的是殘差，即觀測值和預測值之間的差值 A = y-f (x) 因此，前者可以擴展到:

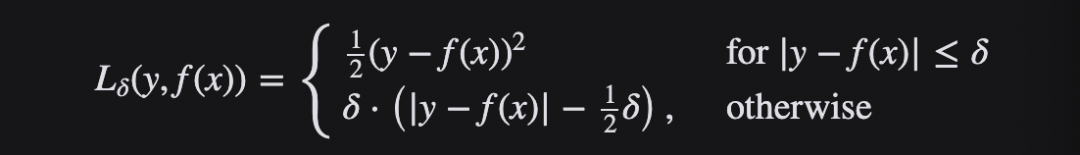
總之，Huber Loss 增強了MSE的離群點魯棒性，減小了對離群點的敏感度問題。當誤差較大時 ，使用MAE可降低異常值影響，使得訓練更加健壯。其下降速度介于MAE與MSE之間，彌補了MAE在Loss下降速度慢的問題，而更接近MSE。

小結

在神經網絡中，損失函數是神經網絡的預測輸出與實際輸出之間差異的度量，計算當前輸出和預期輸出之間的距離。這是一種評估如何建模數據的方法，提供了神經網絡表現如何的度量，并被用作訓練期間優化的目標。損失函數越小，一般就代表模型的魯棒性越好，正是損失函數指導了模型的學習。

【參考資料與關聯閱讀】

• PolyLoss: A Polynomial Expansion Perspective of Classification Loss Functions ，https://arxiv.org/abs/2204.12511
• Focal Loss for Dense Object Detection ，https://arxiv.org/abs/1708.02002
• Generalized End-to-End Loss for Speaker Verification ，https://arxiv.org/abs/1710.10467
• ArcFace: Additive Angular Margin Loss for Deep Face Recognition ，https://arxiv.org/abs/1801.07698
• FaceNet: A Unified Embedding for Face Recognition and Clustering，https://arxiv.org/abs/1503.03832
• Contrastive Predictive Coding，https://arxiv.org/pdf/1807.03748v2.pdf
• Rethinking Dice Loss for Medical Image Segmentation，https://ieeexplore.ieee.org/document/9338261
• Adaptive Margin Ranking Loss for Knowledge Graph Embeddings via a Correntropy Objective Function，https://arxiv.org/pdf/1907.05336.pdf
• Multiple Negative Ranking Loss，https://arxiv.org/pdf/1705.00652.pdf
• Contrastive Loss，http://yann.lecun.com/exdb/publis/pdf/hadsell-chopra-lecun-06.pdf