手把手教你用Python進行帕累托分析(二八定律)
同樣的投入放在不同的地方會產生不同的效益。例如,對一個公司來講,80%的利潤常常來自于20%最暢銷的產品,而其他80%的產品只產生了20%的利潤。
就餐飲企業來講,應用貢獻度分析可以重點改善某菜系盈利最高的前80%的菜品,或者重點發展綜合影響最高的80%的部門。這種結果可以通過帕累托圖直觀地呈現出來。圖3-10是某個月中海鮮系列的10個菜品A1~A10的盈利額(已按照從大到小的順序排序)。
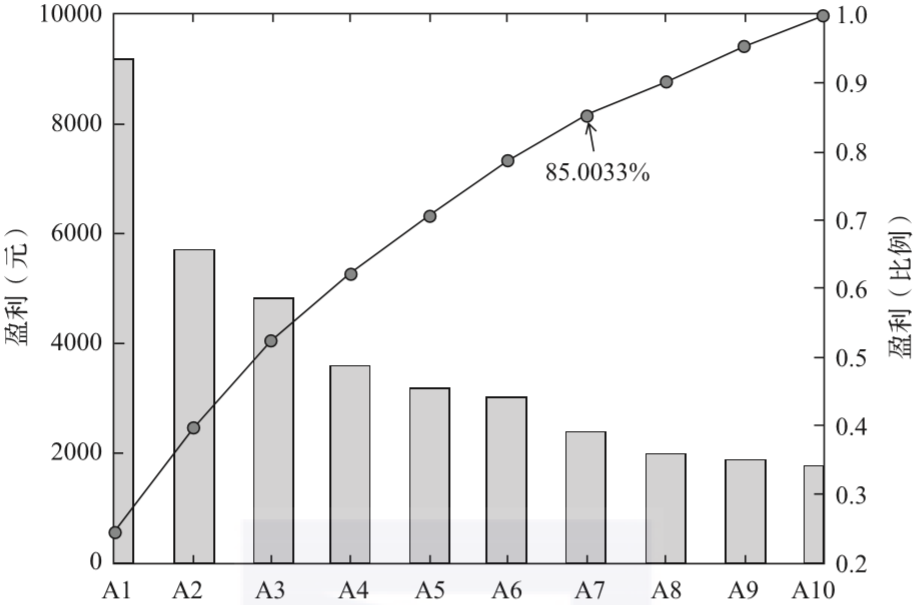
圖3-10 菜品盈利數據帕累托圖
由圖3-10可知,菜品A1~A7共7個菜品,占菜品種類數的70%,總盈利額占該月盈利額的85.0033%。根據帕累托法則,應該增加對菜品A1~A7的成本投入,減少對菜品A8~A10的成本投入,以獲得更高的盈利額。
表3-5是餐飲系統對應的菜品盈利數據,繪制菜品盈利帕累托圖,如代碼清單3-8所示。
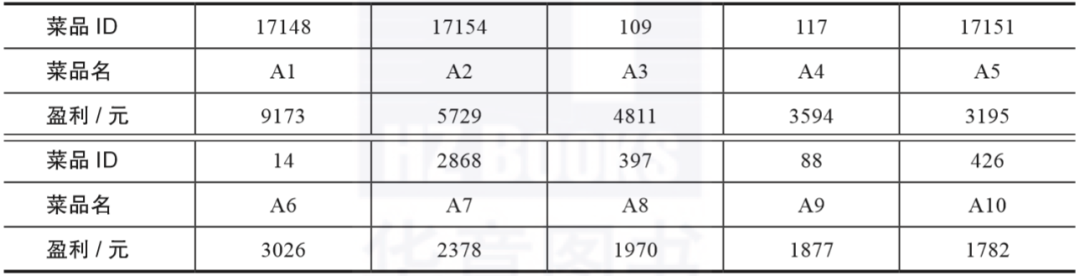
表3-5 餐飲系統菜品盈利數據
代碼清單3-8 繪制菜品盈利數據帕累托圖
- # 菜品盈利數據帕累托圖
- import pandas as pd
- # 初始化參數
- dish_profit = '../data/catering_dish_profit.xls'# 餐飲菜品盈利數據
- data = pd.read_excel(dish_profit, index_col='菜品名')
- datadata = data['盈利'].copy()
- data.sort_values(ascending=False)
- import matplotlib.pyplot as plt # 導入圖像庫
- plt.rcParams['font.sans-serif'] = ['SimHei'] # 用來正常顯示中文標簽
- plt.rcParams['axes.unicode_minus'] = False # 用來正常顯示負號
- plt.figure()
- data.plot(kind='bar')
- plt.ylabel('盈利(元)')
- p = 1.0*data.cumsum()/data.sum()
- p.plot(color='r', secondary_y=True, style='-o',linewidth=2)
- plt.annotate(format(p[6], '.4%'), xy=(6, p[6]), xytext=(6*0.9, p[6]*0.9), arrow-props=dict(arrowstyle="->", connectionstyle="arc3,rad=.2"))
- # 添加注釋,即85%處的標記。這里包括了指定箭頭樣式。
- plt.ylabel('盈利(比例)')
- plt.show()