深度學習入門自編碼器到變分自編碼器
自編碼器(autoencoder, AE)是一類在半監督學習和非監督學習中使用的人工神經網絡(Artificial Neural Networks, ANNs),屬于深度學習領域的范疇,其功能是通過將輸入信息作為學習目標,對輸入信息進行表征學習。通常用于壓縮降維,風格遷移和離群值檢測等等。對于圖像而言,圖像的數據分布信息可以高效表示為編碼,但是其維度和數據信息一般遠小于輸入數據,可作為強大的特征提取器,適用于深度神經網絡的預訓練,此外它還可以隨機生成與訓練數據類似的數據,以此來高效率的表達原數據的重要信息,因此通常被看作是生成模型。
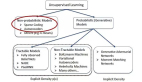
自編碼器在深度學習的發展過程中出現了很多變體,比如演化出去噪自編碼器再到變分自編碼器(Denoising Autoencoder,DAE),再到變分自編碼器(Variational auto-encoder,VAE),最后到去耦變分自編碼,隨著時代的發展,往后會出現更多優秀的模型,但它的原理從數學角度都是從輸入空間和特征空間開始,自編碼器求解兩者的映射的相似性誤差,通過以下公式使其最小化.
求解完成之后,自編碼器輸出計算后的特征h,即編碼特征,但在自編碼運算過程中,容易混入一些隨機性,在公式中標識為高斯噪聲,然后將編碼器的輸出作為下一道解碼器的輸入特征,最終得到一個生成后的數據分布信息。
簡單的架構如下所示,以變分自編碼器(Variational auto-encoder,VAE)為例。
接下來,按照條理邏輯分別介紹。
1.自編碼器(AE):
自編碼器分成兩個部分,第一個部分是encoder,一般是多層網絡,將輸入的數據壓縮成為一個向量,變成低維度,而該向量就稱之為瓶頸。第二個部分是decoder,灌之以瓶頸,輸出數據,我們稱之為重建輸入數據。我們的目的是要讓重建數據和原數據一樣,以達到壓縮還原的作用。損失函數就是讓重建數據和原數據距離最小即可。損失函數參考圖3。
下圖是一次訓練一個淺層自編碼器
首先,第一個自編碼器學習去重建輸入。然后,第二個自編碼器學習去重建第一個自編碼器隱層的輸出。最后,這兩個自編碼器被整合到一起。缺點:低維度的瓶頸顯然丟失了很多有用的信息,重建的數據效果并不好。
2.去噪自編碼器(DAE)
這里要講的是,我們拿到一張干凈的圖片,想象一下比如是干凈的原始minst數據集,此時我們給原來干凈的圖片集加上很多噪聲,灌給編碼器,我們希望可以還原成干凈的是圖片集,以和AE相同的方式去訓練,得到的網絡模型便是DAE.
如上圖,去噪編碼器一般對最初輸入增加噪聲,通過訓練之后得到無噪聲的輸出。這防止了自編碼器簡單的將輸入復制到輸出,從而提取出數據中有用的模式。增加噪聲方式可以通過圖6左側增加高斯噪聲,或者通過圖6右側的droupout,直接丟棄掉一層特征。
3.變分自編碼器VAE
VAE和AE,DAE不同的是,原先編碼器是映射成一個向量,現在是映射成兩個向量,一個向量表示分布的平均值,另外一個表示分布的標準差,兩個向量都是相同的正太分布。現在從兩個向量分別采樣,采樣的數據灌給解碼器。于是我們得到了損失函數:
損失函數的前部分和其他自編碼器函數一樣是重建loss損失,后部分是KL散度。KL散度是衡量兩個不同分布的差異,有個重要的性質是總是非負的。僅當兩個分布式完全相同的時候才是0。所以后部分的作用就是控制瓶頸處的兩個向量處于正態分布。(均值為0,標準差為1)。這里有一個問題,從兩個分布采樣數據,BP時候怎么做?所以有一個技巧叫做參數重現(Reparameterization Trick),前向傳播的時候,我們是通過以上公式得到z,BP的時候是讓神經網絡去擬合μ和σ,一般我們很難求的參數都丟給神經網絡就好,就像Batch Normonization的γ和β一樣。缺點效果還是比較模糊。
4.去耦變分自編碼
我們希望瓶頸處的向量,即低維度的向量把編碼過程中有用的維度保留下來,把沒有用的維度用正態分布的噪聲替代,可以理解為學習不同維度的特征,只是這些特征有好壞之分而已。我們僅需在loss function中加上一個β即可達到目的。
最后實驗表明,VAE在重建圖片時候對圖片的<長度,寬度,大小,角度>四個值時候是混亂的,而去耦變分自編碼器是能比較清晰的展示,最后生成的圖片效果也更銳利清楚。至此,非常簡單明了的介紹完了自編碼到去噪自編碼器到變分自編碼器到去耦變分自編碼。