如何使用TensorFlow和自編碼器模型生成手寫數字
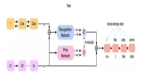
自編碼器是一種能夠用來學習對輸入數據高效編碼的神經網絡。若給定一些輸入,神經網絡首先會使用一系列的變換來將數據映射到低維空間,這部分神經網絡就被稱為編碼器。
然后,網絡會使用被編碼的低維數據去嘗試重建輸入,這部分網絡稱之為解碼器。我們可以使用編碼器將數據壓縮為神經網絡可以理解的類型。然而自編碼器很少用做這個目的,因為通常存在比它更為有效的手工編寫的算法(例如 jpg 壓縮)。
此外,自編碼器還被經常用來執行降噪任務,它能夠學會如何重建原始圖像。
什么是變分自編碼器?
有很多與自編碼器相關的有趣應用。
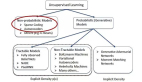
其中之一被稱為變分自編碼器(variational autoencoder)。使用變分自編碼器不僅可以壓縮數據–還能生成自編碼器曾經遇到過的新對象。
使用通用自編碼器的時候,我們根本不知道網絡所生成的編碼具體是什么。雖然我們可以對比不同的編碼對象,但是要理解它內部編碼的方式幾乎是不可能的。這也就意味著我們不能使用編碼器來生成新的對象。我們甚至連輸入應該是什么樣子的都不知道。
而我們用相反的方法使用變分自編碼器。我們不會嘗試著去關注隱含向量所服從的分布,只需要告訴網絡我們想讓這個分布轉換為什么樣子就行了。
通常情況,我們會限制網絡來生成具有單位正態分布性質的隱含向量。然后,在嘗試生成數據的時候,我們只需要從這種分布中進行采樣,然后把樣本喂給解碼器就行,解碼器會返回新的對象,看上去就和我們用來訓練網絡的對象一樣。
下面我們將介紹如何使用 Python 和 TensorFlow 實現這一過程,我們要教會我們的網絡來畫 MNIST 字符。
第一步加載訓練數據
首先我們來執行一些基本的導入操作。TensorFlow 具有非常便利的函數來讓我們能夠很容易地訪問 MNIST 數據集。
- import tensorflow as tfimport numpy as npimport matplotlib.pyplot as plt
- %matplotlib inlinefrom tensorflow.examples.tutorials.mnist import input_data
- mnist = input_data.read_data_sets('MNIST_data')
定義輸入數據和輸出數據
MNIST 圖像的維度是 28*28 像素,只有單色通道。我們的輸入數據 X_in 是一批一批的 MNIST 字符,網絡會學習如何重建它們。然后在一個占位符 Y 中輸出它們,輸出和輸入具有相同的維度。
Y_flat 將會在后面計算損失函數的時候用到,keep_prob 將會在應用 dropout 的時候用到(作為一種正則化的方法)。在訓練的過程中,它的值會設為 0.8,當生成新數據的時候,我們不使用 dropout,所以它的值會變成 1。
lrelu 函數需要自及定義,因為 TensorFlow 中并沒有預定義一個 Leaky ReLU 函數。
- tf.reset_default_graph()
- batch_size = 64X_in = tf.placeholder(dtype=tf.float32, shape=[None, 28, 28], name='X')
- Y = tf.placeholder(dtype=tf.float32, shape=[None, 28, 28], name='Y')
- Y_flat = tf.reshape(Y, shape=[-1, 28 * 28])
- keep_prob = tf.placeholder(dtype=tf.float32, shape=(), name='keep_prob')
- dec_in_channels = 1n_latent = 8reshaped_dim = [-1, 7, 7, dec_in_channels]
- inputs_decoder = 49 * dec_in_channels / 2def lrelu(x, alpha=0.3): return tf.maximum(x, tf.multiply(x, alpha))
定義編碼器
因為我們的輸入是圖像,所以使用一些卷積變換會更加合理。最值得注意的是我們在編碼器中創建了兩個向量,因為編碼器應該創建服從高斯分布的對象。
- 一個是均值向量
- 一個是標準差向量
在后面你會看到,我們是如何「強制」編碼器來保證它確實生成 了服從正態分布的數據點,我們可以把將會被輸入到解碼器中的編碼值表示為 z。在計算損失函數的時候,我們會需要我們所選分布的均值和標準差。
- def encoder(X_in, keep_prob):
- activation = lrelu with tf.variable_scope("encoder", reuse=None):
- X = tf.reshape(X_in, shape=[-1, 28, 28, 1])
- x = tf.layers.conv2d(X, filters=64, kernel_size=4, strides=2, padding='same', activation=activation)
- x = tf.nn.dropout(x, keep_prob)
- x = tf.layers.conv2d(x, filters=64, kernel_size=4, strides=2, padding='same', activation=activation)
- x = tf.nn.dropout(x, keep_prob)
- x = tf.layers.conv2d(x, filters=64, kernel_size=4, strides=1, padding='same', activation=activation)
- x = tf.nn.dropout(x, keep_prob)
- x = tf.contrib.layers.flatten(x)
- mn = tf.layers.dense(x, units=n_latent)
- sd = 0.5 * tf.layers.dense(x, units=n_latent)
- epsilon = tf.random_normal(tf.stack([tf.shape(x)[0], n_latent]))
- z = mn + tf.multiply(epsilon, tf.exp(sd))
- return z, mn, sd
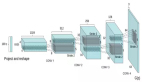
定義解碼器
解碼器不會關心輸入值是不是從我們定義的某個特定分布中采樣得到的。它僅僅會嘗試重建輸入圖像。最后,我們使用了一系列的轉置卷積(transpose convolution)。
- def decoder(sampled_z, keep_prob): with tf.variable_scope("decoder", reuse=None):
- x = tf.layers.dense(sampled_z, units=inputs_decoder, activation=lrelu)
- x = tf.layers.dense(x, units=inputs_decoder * 2 + 1, activation=lrelu)
- x = tf.reshape(x, reshaped_dim)
- x = tf.layers.conv2d_transpose(x, filters=64, kernel_size=4, strides=2, padding='same', activation=tf.nn.relu)
- x = tf.nn.dropout(x, keep_prob)
- x = tf.layers.conv2d_transpose(x, filters=64, kernel_size=4, strides=1, padding='same', activation=tf.nn.relu)
- x = tf.nn.dropout(x, keep_prob)
- x = tf.layers.conv2d_transpose(x, filters=64, kernel_size=4, strides=1, padding='same', activation=tf.nn.relu)
- x = tf.contrib.layers.flatten(x)
- x = tf.layers.dense(x, units=28*28, activation=tf.nn.sigmoid)
- img = tf.reshape(x, shape=[-1, 28, 28]) return img
現在,我們將兩部分連在一起。
- sampled, mn, sd = encoder(X_in, keep_prob)
- dec = decoder(sampled, keep_prob)
計算損失函數,并實施一個高斯隱藏分布
為了計算圖像重構的損失函數,我們簡單地使用了平方差(這有時候會使圖像變得有些模糊)。這個損失函數還結合了 KL 散度,這確保了我們的隱藏值將會從一個標準分布中采樣。關于這個主題,如果想要了解更多,可以看一下這篇文章(https://jaan.io/what-is-variational-autoencoder-vae-tutorial/)。
- unreshaped = tf.reshape(dec, [-1, 28*28])
- img_loss = tf.reduce_sum(tf.squared_difference(unreshaped, Y_flat), 1)
- latent_loss = -0.5 * tf.reduce_sum(1.0 + 2.0 * sd - tf.square(mn) - tf.exp(2.0 * sd), 1)
- loss = tf.reduce_mean(img_loss + latent_loss)
- optimizer = tf.train.AdamOptimizer(0.0005).minimize(loss)
- sess = tf.Session()
- sess.run(tf.global_variables_initializer())
訓練網絡
現在我們終于可以訓練我們的 VAE 了!
每隔 200 步,我們會看一下當前的重建是什么樣子的。大約在處理了 2000 次迭代后,大多數重建看上去是挺合理的。
- for i in range(30000):
- batch = [np.reshape(b, [28, 28]) for b in mnist.train.next_batch(batch_size=batch_size)[0]]
- sess.run(optimizer, feed_dict = {X_in: batch, Y: batch, keep_prob: 0.8})
- if not i % 200:
- ls, d, i_ls, d_ls, mu, sigm = sess.run([loss, dec, img_loss, dst_loss, mn, sd], feed_dict = {X_in: batch, Y: batch, keep_prob: 1.0})
- plt.imshow(np.reshape(batch[0], [28, 28]), cmap='gray')
- plt.show()
- plt.imshow(d[0], cmap='gray')
- plt.show()
- print(i, ls, np.mean(i_ls), np.mean(d_ls))
生成新數據
最驚人的是我們現在可以生成新的字符了。最后,我們僅僅是從一個單位正態分布里面采集了一個值,輸入到解碼器。生成的大多數字符都和人類手寫的是一樣的。
- randoms = [np.random.normal(0, 1, n_latent) for _ in range(10)]
- imgs = sess.run(dec, feed_dict = {sampled: randoms, keep_prob: 1.0})
- imgs = [np.reshape(imgs[i], [28, 28]) for i in range(len(imgs))]for img in imgs:
- plt.figure(figsize=(1,1))
- plt.axis('off')
- plt.imshow(img, cmap='gray')
一些自動生成的字符。
總結
這是關于 VAE 應用一個相當簡單的例子。但是可以想象一下更多的可能性!神經網絡可以學習譜寫音樂,它們可以自動地創建對書籍、游戲的描述。借用創新思維,VAE 可以為一些新穎的項目開創空間。