「算法與數據結構」帶你看回溯算法之美
前言
這次梳理的是回溯算法,掌握它的解決問題思路,對很多搜索嘗試問題,都會在日后學習工作中有所幫助。
我對回溯算法有一定理解:回溯算法建立在DFS基礎之上的,但不同的是在搜索的過程中,達到結束條件后,恢復狀態,回溯上一層,再次搜索,因此我們可以這樣子理解,回溯算法與DFS的區別就是有無狀態重置。
如果你還不了解什么是回溯算法,或者知道一些,但是對于它具體是如何實現回溯,那么這篇文章可能適合你閱讀。
那么圍繞以下幾個點來展開介紹回溯算法👇
- 來源
- 基本思路
- 算法框架
- 經典例題
回溯算法的來源
首先,我們得明白啥叫回溯算法,它的由來是什么。
根據維基百科給出的定義👇
回溯算法也叫試探法,它是一種系統地搜索問題的解的方法。
用回溯算法解決問題的一般步驟:
1、 針對所給問題,定義問題的解空間,它至少包含問題的一個(最優)解。
2 、確定易于搜索的解空間結構,使得能用回溯法方便地搜索整個解空間 。
3 、以深度優先的方式搜索解空間,并且在搜索過程中用剪枝函數避免無效搜索。
用更加簡單的話術來解釋的話👇
回溯法可以理解成為通過選擇不同的岔路口,來尋找目的地,一個岔路口一個岔路口的去嘗試找到目的地,如果走錯了路的話,繼續返回到上一個岔路口的另外一條路,直到找到目的地。
基本思路
首先,我們得明確這個回溯算法的思路是什么,有了思路,我們才可以根據這個思路寫出偽代碼,有了偽代碼之后,根據實際的問題,寫出相應的解決方案。
我們可以把這類回溯問題,看成是解決一個決策樹的遍歷過程,這樣子也方便我們接下來的解釋👇
基本思路:
- 從決策樹的一條路開始走,能進則進,不能進則退回來,換一條路試一試。
舉個例子來說,還是拿八皇后問題來解釋:
- 第一步按照順利,也就是在第一行,我們放置第一個皇后。
- 第二步,我們需要在第二行放置一個皇后,我們需要遍歷,將符合要求的位置放置皇后。
- 第三步,也就是在第三行,我們需要去遍歷,找到符合的位置,如果都沒有符合要求,我們就需要「撤銷第二步操作」,那么需要改變第二個皇后位置,重新放置第二個皇后位置,直到滿足第三個皇后放置的位置。
- 當你改變第二個皇后位置后,都無法滿足第三個皇后位置的時候,我們就需要「撤銷第一步操作」,重新去放置第一個皇后位置,然后按照順序完成后續操作。
我們可以通過另外一個例子來看,也就是回溯在迷宮搜索中也很常見,簡單來說,就是這條路走不通的話,我們就需要「撤銷上個操作」,返回前一個路口,繼續下一條路。
似乎你已經發現了,回溯說到底就是「窮舉法」,但是如果你只是單純的窮舉的話,不剪枝的話,時間復雜度是巨大的,那么如何剪枝呢?
我們將回溯優化的方法可以稱之為剪枝,或者是剪枝函數,通過這個函數,我們可以減去一些狀態,剪去一些不可能到達(「最終狀態」),這里說的最終狀態,可以認為是答案狀態,這樣子的話,就減少了部分空間樹節點的生成,具體如何剪枝的話,可以根據做題經驗多加練習,這里就不張開了。
算法框架
其實刷了一定的題量,你會發現,對于這種回溯思路而言,都是有一定的套路的,那么接下來就給出偽代碼👇
接下來是自己的一點理解,覺得按照這個步驟來的話,也好理解一些👇
可以按照3個步驟來思考這類的問題:
- 「路徑」:記錄做出的選擇。
- 「選擇列表」:通常而言,用數組存儲可以選擇的操作。
- 「結束條件」:一般而言,就是遞歸的結束點,也就是搜索的結束點。
- result = []
- function backtrack(路徑, 選擇列表) {
- if('滿足結束條件') {
- // 這里就是對答案做更新,依據實際題目出發
- result.push(路徑)
- return
- } else {
- for(let i = 0; i < 選擇列表.length; i++) {
- // 對一個選擇列表做相應的選擇
- 做選擇
- backtrack(路徑, 選擇列表)
- // 既然是回溯算法,那么在一次分岔路做完選擇后
- // 需要回退我們之前做的操作
- 撤銷選擇
- }
- }
- }
做過類似的題目都知道,核心的處理就是for循環里面的遞歸操作,每次在遞歸之前,「做選擇」,在這種方案結束后,我們需要「撤銷選擇」,這樣子的話,就不會影響同一層決策樹的其他選擇。
舉個例子,在走迷宮這類題型中,我們需要不斷的去搜索,去試探答案,這個過程就是一個回溯算法的過程,每次要走下一個格子的時候,我們需要先將這個格子「做個標記」,代表這個格子已經走過,然后在往后繼續搜索...
當這個方案不合理的時候,我們是不是需要將之前標記的格子清除標記呢?仔細想一想的話,這樣子是非常合理的,在當前方案行不通的時候,我們要將這個「步驟撤銷掉」。
對于以上的基礎知識,有了一定了解,接下來我們就通過這么基礎知識來解決問題。
怎么樣寫回溯
做一些題目后,對回溯算法有初步認識后,我覺得可以參考下面的步驟來刻意練習👇
- 首先畫出遞歸樹,找到狀態變量(這里可以理解成回溯函數參數)。
- 確定遞歸出口,一般根據具體題目條件而言。
- 找準選擇列表(一般而言與函數參數有關)。
- 剪枝,對于一些情況而言,可以適當剪枝。
- 做出選擇,遞歸調用,進入下一層。
- 撤銷選擇。
我覺得這個對回溯算法的總結,是挺不錯的,可以借鑒下。
2個例子
接下來,我們通過三個題目作為例子,來看看怎么根據我們之前提及的算法框架來解決問題👇
字母大小寫全排列⭐
鏈接:字母大小寫全排列
給定一個字符串S,通過將字符串S中的每個字母轉變大小寫,我們可以獲得一個新的字符串。返回所有可能得到的字符串集合。
示例:
輸入:S = "a1b2" 輸出:["a1b2", "a1B2", "A1b2", "A1B2"]
輸入:S = "3z4" 輸出:["3z4", "3Z4"]
輸入:S = "12345" 輸出:["12345"]
提示:
S 的長度不超過12。S 僅由數字和字母組成。
來源:力扣(LeetCode) 鏈接:https://leetcode-cn.com/problems/letter-case-permutation 著作權歸領扣網絡所有。商業轉載請聯系官方授權,非商業轉載請注明出處。
嗯,這題的話,可以通過畫圖舉個例子來說,我這里就借鑒網上的圖了👇
字母全排列
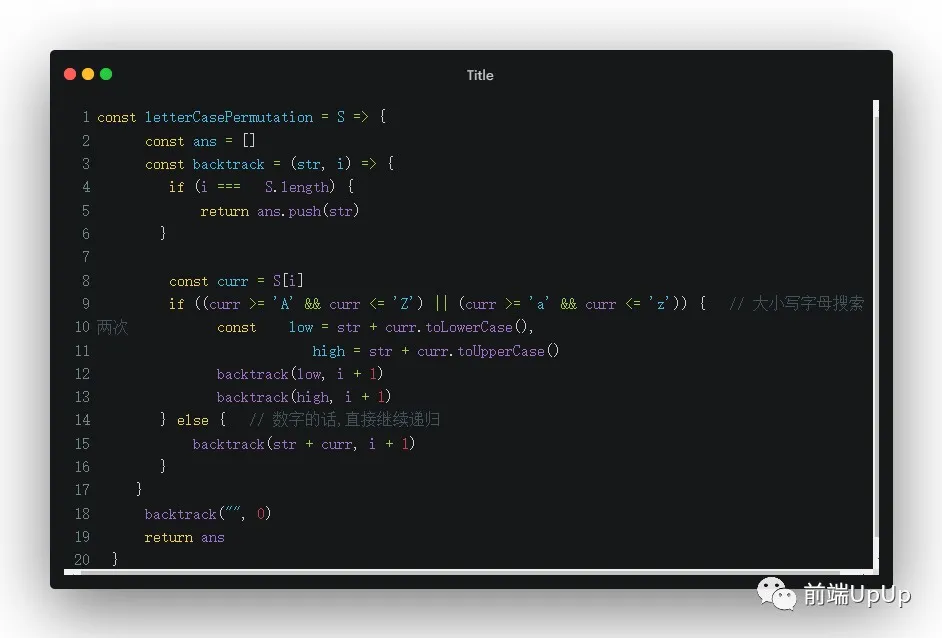
對于數字而言的話,我們直接跳過,字母的話,無非就是兩種狀態,大小寫字母,那么我們就有接下來的思路👇
- 遇到數字的話,不會涉及新的分支,我們就直接往后搜,這樣子的話,對于數字就只需要搜索一次。
- 對于單個字母而言,我們需要「搜索2次」,小寫字母搜索一次,大寫字母搜索一次。
- 我們可以去維護一個index,遇到數字的話,index+1,繼續遞歸,遇到字母的話,需要遞歸兩次,假設當字母是小寫時,我們遞歸一次(index+1),然后回溯時將字母轉為大寫,又去遞歸一次。
- 遞歸盡頭:即搜索完整個字符串為止,我們前面維護的index,這個時候就可以作為條件判斷。
按照這個思路走的話,我們就可以寫出完整的解題代碼
代碼👇
回溯算法代碼-1
代碼點這里☑️
子集🐍⭐⭐
鏈接:子集
給定一組不含重復元素的整數數組 nums,返回該數組所有可能的子集(冪集)。
說明:解集不能包含重復的子集。
示例:
輸入: nums = [1,2,3] 輸出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]
來源:力扣(LeetCode) 鏈接:https://leetcode-cn.com/problems/subsets 著作權歸領扣網絡所有。商業轉載請聯系官方授權,非商業轉載請注明出處。
做這類題目的時候,不太懂的話,可以先畫圖,從上面的題來看,我們可以畫類似一個樹的結構,然后看看如何去遍歷這個決策樹,看看能不能剪枝,直接借鑒一下網上的圖👇
子集的遞歸樹
其實把這個圖畫出來,你應該就成功一半了,從這個圖來看,我們似乎又可以去遍歷這顆樹。
首先我們得把我們思路整理一下👇
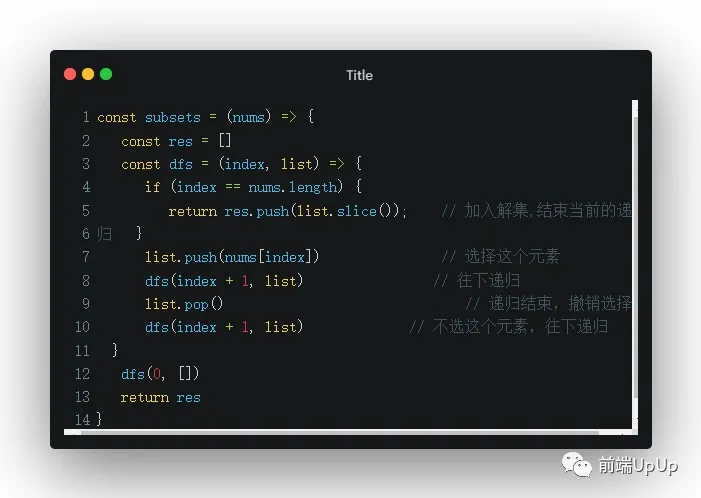
- 這題肯定是求樹的所有節點!
- 對這顆樹而言,我們可以遍歷它的分支,選擇其中一個分支,然后繼續向下操作,不選這個分支的話,選擇另外一個分支又是另外一個情況,所以每次枚舉下一個數字的時候,也就是兩種選擇:選或不選。
- 可以考慮使用一個index指針來記錄「節點」的狀態,即當前遞歸考察的數字nums[index]
- 遞歸結束的條件:index === nums.length, 這個時候代表考察完所有的數字,把當前的子集加入題解,結束當前遞歸分支。
- 每次結束一個分支,即結束遞歸,需要撤銷當前的選擇,(從list中刪除),回到選擇前的狀態,做另外一個選擇,即不選擇當前的數字,往下遞歸,繼續生成子集。
根據以上的偽代碼,我們基本上就能解出這個題目👇
回溯算法題解-2
代碼點這里☑️
題目是做不完的,做完這些題目后,希望你能找出回溯算法的規律,能對它有更加深入的理解~,接下來準備了些題集,希望對你們有幫助~
進階題目匯總
以下是我在網上看到一套不錯的回溯算法題集,如果你還在刻意找的話,可以看看這里。