每日算法:二叉樹的最近公共祖先
本文轉載自微信公眾號「三分鐘學前端」,作者sisterAn。轉載本文請聯系三分鐘學前端公眾號。
關于樹基礎看這里:適合初學者的樹
給定一個二叉樹, 找到該樹中兩個指定節點的最近公共祖先。
百度百科中最近公共祖先的定義為:“對于有根樹 T 的兩個結點 p、q,最近公共祖先表示為一個結點 x,滿足 x 是 p、q 的祖先且 x 的深度盡可能大(一個節點也可以是它自己的祖先)。”
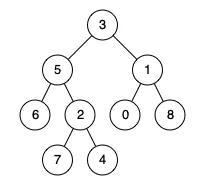
例如,給定如下二叉樹: root = [3,5,1,6,2,0,8,null,null,7,4]
示例 1:
- 輸入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 1
- 輸出: 3
- 解釋: 節點 5 和節點 1 的最近公共祖先是節點 3。
示例 2:
- 輸入: root = [3,5,1,6,2,0,8,null,null,7,4], p = 5, q = 4
- 輸出: 5
- 解釋: 節點 5 和節點 4 的最近公共祖先是節點 5。因為根據定義最近公共祖先節點可以為節點本身。
說明:
- 所有節點的值都是唯一的。
- p、q 為不同節點且均存在于給定的二叉樹中。
解答:遞歸實現
解題思路:
如果樹為空樹或 p 、 q 中任一節點為根節點,那么 p 、 q 的最近公共節點為根節點
如果不是,即二叉樹不為空樹,且 p 、 q 為非根節點,則遞歸遍歷左右子樹,獲取左右子樹的最近公共祖先,
- 如果 p 、 q 節點在左右子樹的最近公共祖先都存在,說明 p 、 q 節點分布在左右子樹的根節點上,此時二叉樹的最近公共祖先為 root
- 若 p 、 q 節點在左子樹最近公共祖先為空,那 p 、q 節點位于左子樹上,最終二叉樹的最近公共祖先為右子樹上 p 、q 節點的最近公共祖先
- 若 p 、 q 節點在右子樹最近公共祖先為空,同左子樹 p 、 q 節點的最近公共祖先為空一樣的判定邏輯
- 如果 p 、 q 節點在左右子樹的最近公共祖先都為空,則返回 null
代碼實現:
- const lowestCommonAncestor = function(root, p, q) {
- if(root == null || root == p || root == q) return root
- const left = lowestCommonAncestor(root.left, p, q)
- const right = lowestCommonAncestor(root.right, p, q)
- if(left === null) return right
- if(right === null) return left
- return root
- };
復雜度分析:
時間復雜度:O(n)
空間復雜度:O(n)