北大計算機博士生先于OpenAI發表預訓練語言模型求解數學題論文
最近,EMNLP 2021開獎了!華人作者包攬了最佳長、短論文。
然而,有人歡喜有人憂。
北大博士生沈劍豪領銜的一篇關于「用語言模型來解決數學應用題」(Generate & rank: A multi-task framework for math word problems)的EMNLP投稿在綜合評審時被認為不夠重要,最終收錄于Findings而沒有被主會接收。

「審稿人普遍喜歡這篇論文,但這看起來是一篇邊緣的論文。鑒于這是BART在數學問題上的應用,而數學問題的解決對于NLP來說并不是一個真正重要的任務,我懷疑這個任務的高度工程化解決方案的價值。」
根據官方的文件來看,一般被列為Findings的論文得分會更低一些,或者被認為不怎么「新穎」。

拓展了特定任務的SOTA,但是對EMNLP社區而言,沒有新的見解或更廣泛的適用性;
有良好的、新穎的實驗,并提出了全面的分析和結論,但使用的方法不夠「新穎」。
雖然,但是OpenAI覺得這個論文很重要
有趣的是,就在10月29號,OpenAI提出了一個新方法「驗證」(verification),聲稱可以解決小學數學問題。

論文地址:https://arxiv.org/pdf/2110.14168.pdf
GSM8K數據集地址:https://github.com/openai/grade-school-math
OpenAI要解決的數學應用題是長這個樣子滴:

OpenAI的GSM8K數據集中的三個問題示例,紅色為計算的注釋
而且,OpenAI發現「驗證」可以讓60億參數的GPT-3,解數學應用題的準確率直接翻倍,甚至追平了1750億參數,采用微調方法的GPT-3模型。
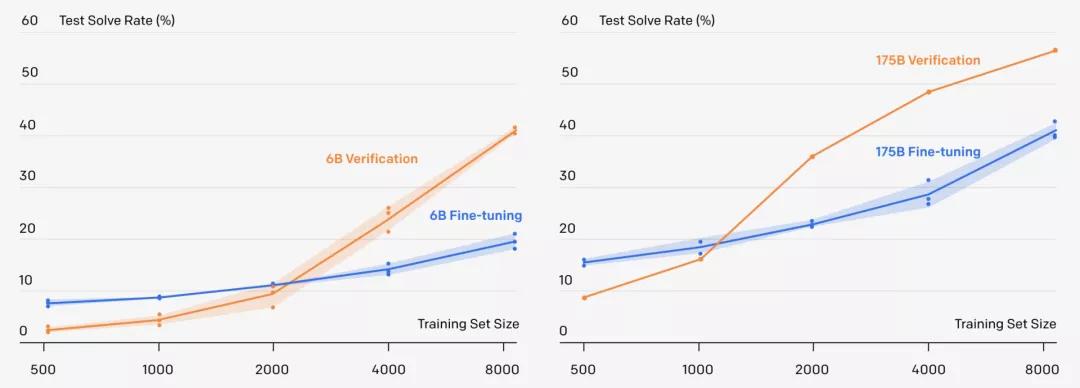
更重要的是,一個9-12歲的小孩子在測試中得分為60分,而OpenAI的方法在同樣的問題上可以拿到55分,已經達到了人類小學生90%左右的水平!
都是解決數學應用題,那會不會這兩篇文章是「異曲同工」呢?
巧了,還真是!
不僅如此,OpenAI這個最新工作《Training Verifiers to Solve Math Word Problems》文中還引用了北大博士生沈劍豪在9月7號提交的《Generate & Rank: A Multi-task Framework for Math Word Problems》這篇論文。

沈劍豪,尹伊淳,李琳,尚利峰,蔣欣,張銘, 劉群,《生成&排序:一種數學文字問題的多任務框架》,EMNLP 2020 Findings。該工作由北大計算機學院和華為諾亞方舟實驗室合作完成。
論文地址:https://arxiv.org/abs/2109.03034
再看看沈同學文中要解決的數學應用題長啥樣。
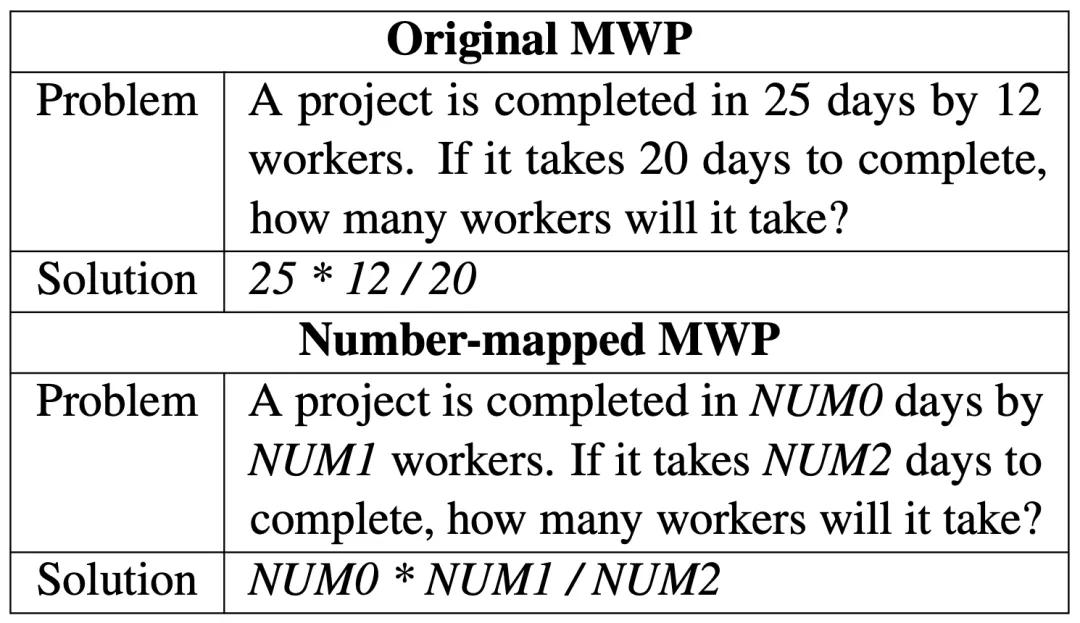
兩者確實很像啊!
深入OpenAI的論文的Introduction部分,可以找到下面這句話。
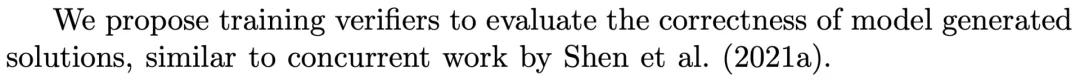
OpenAI在論文中表示其思路和沈劍豪的論文相似
在Related Methods中,還可以看到下面這句。

我們的工作與他們的方法有許多基本相似之處,盡管我們在幾個關鍵方面有所不同。
在文末,OpenAI也對沈博士的文章注明了引用。

也就是說,OpenAI認可了沈同學文中的方法的價值,而且沈劍豪的論文其實比OpenAI還要早發一個月!
值得一說的是,這篇論文的一作沈劍豪是2014年浙江省高考狀元,同時也曾是北大數學學院數據方向的第一名,目前是北大計算機學院在讀博士研究生,導師為張銘教授。
語言模型能解數學題嗎?
OpenAI的GPT-3「文采出眾」,上知天文,下知地理。模仿名家的寫作風格,展示一下廣博的知識,這都不在話下。
然而,GPT-3這種「語言」模型卻是典型的偏科生,擅長文,但不擅理,沒法完成精確的多步推理,比如,解決小學數學應用題。
其問題就在于,語言模型只能模仿正確解決方法的規律,但它卻并不理解「邏輯」。
所以,人類要想教會大語言模型理解復雜的邏輯,就必須得讓模型學會識別它們的錯誤,并仔細選擇他們的解題步驟。
從這個角度出發,OpenAI和博士生沈劍豪都提出了一種「先生成,后排序」的方法來幫助語言模型掌握數學推理能力,知道自己推理是否有誤。
兩者內容對比
核心框架是:生成器+重排序/驗證器。
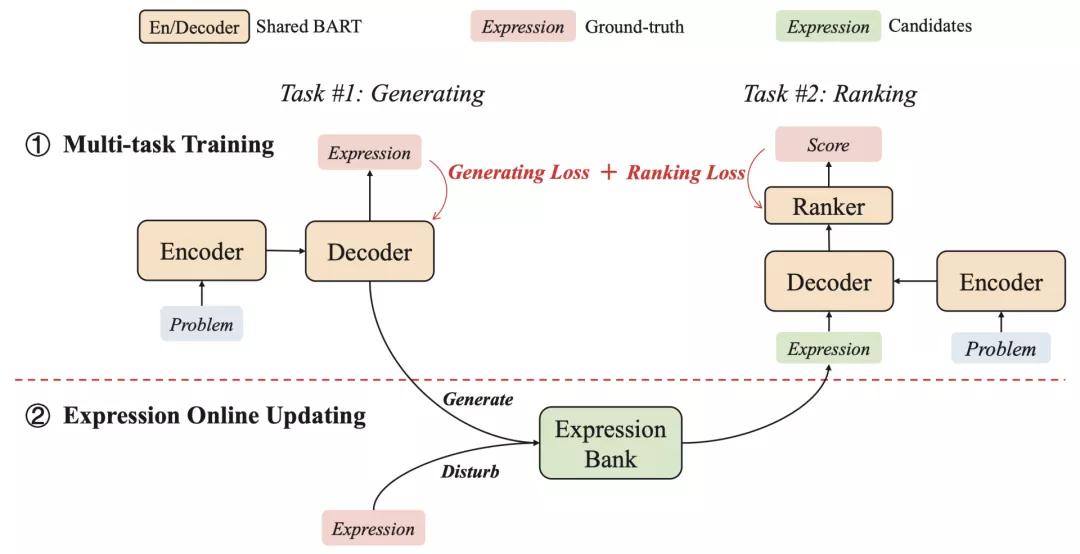
北大與華為諾亞的生成與重排序框架
沈同學文中的模型由一個生成器和一個排序器組成,并通過生成任務和排序任務進行聯合訓練。
生成器的目標是生成給定數學應用題的解答表達式。排序器則需要從一組候選者中選擇一個正確的表達式。
兩者共享同一個的BART模型進行編碼-解碼,排序器在此基礎上增加了一個評分函數為表達式打分。
此外,他們還構建了一個表達式庫,為排序器提供訓練實例。其中使用了兩種不同的策略:基于模型的生成和基于樹的干擾。
基于模型的生成是利用生成器通過線束搜索方法,得到前K個表達式加入到表達式庫中。
基于樹的干擾則首先將正確表達式轉化成一棵二叉樹,然后采用擴展、編輯、刪除、交換四種操作得到新的表達式,作為前一種方法的補充。
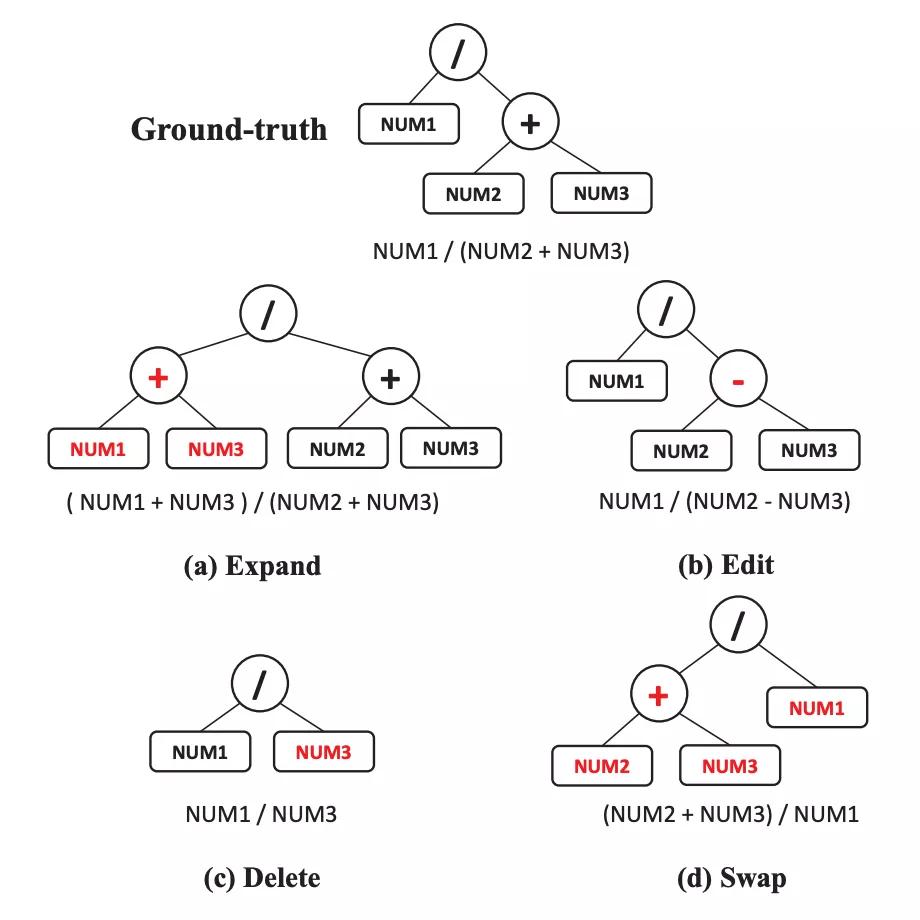
基于樹的干擾
訓練過程包括多任務訓練和表達式在線更新。首先為生成任務對預訓練的BART進行微調。之后,使用經過微調的BART和基于樹的干擾來生成表達式,作為排序器的訓練樣本。然后,進行生成和排序的聯合訓練。
這個過程是以迭代的方式進行的,兩個模塊(即生成器和排序器)繼續相互促進。同時,用于排序器的訓練實例在每輪迭代后會被更新。

Generate & Rank的訓練過程
而OpenAI的方法中是包含一個生成器和一個驗證器。
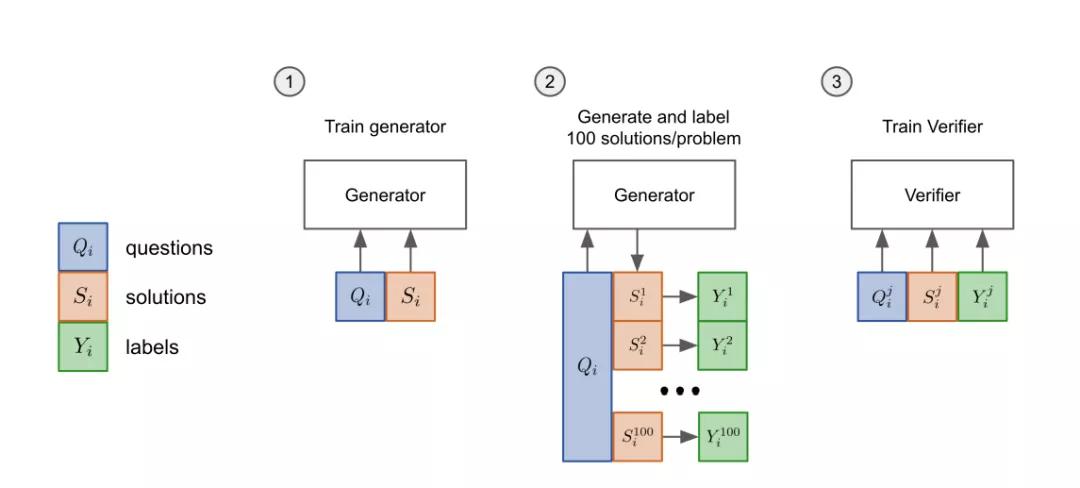
OpenAI的驗證器
驗證器(verifier)可以判斷模型生成的解決方案正不正確,所以在測試時,驗證器會以問題和候選解答為輸入,輸出每個解答正確的概率。驗證器(verifier)訓練時,只訓練解決方案是否達到正確的最終答案,將其標記為正確或不正確。
驗證器具體訓練方法分「三步」:
- 先把模型的「生成器」在訓練集上進行2個epoch的微調。
- 從生成器中為每個訓練問題抽取100個解答,并將每個解答標記為正確或不正確。
- 在數據集上,驗證器再訓練單個epoch。
測試時,解決一個新問題,首先要生成100個候選解決方案,然后由「驗證器」打分,排名最高的解決方案會被最后選中。
思路上確實是相近的,不過有幾處細節并不相同。
一、OpenAI在文中表示他們的生成器和驗證器是分開單獨訓練的,目的是限制生成器的訓練并防止過度擬合,但原則上,他們認為應該可以組合這些模型進行聯合訓練,而沈同學則確實是使用了聯合訓練方法,實驗結果也表明聯合訓練對最終的效果有提升。
二、沈同學提出了一種幫助訓練重排器的方法:Tree-based Disturbance,其實就是設計了一系列比較難的負樣本,在正確的表達式基礎上增加了一點小擾動作為新的負樣本。而OpenAI并沒有提到類似的過程。
三、OpenAI為了評估「驗證器」的表現,收集了全新的「GSM8K數據集」并將其開源以方便研究。
GSM8K由8500個高質量、高多樣性、中等難度的小學數學問題組成。數據集中的每個問題都需要計算2到8個步驟來得出最終答案,涉及到「加減乘除」四則運算。
而沈同學最終是在兩個常用的數據集上進行了實驗:Math23K和MAWPS。
其中,Math23K是一個大規模的中文數據集,包含23162個數學應用題及其對應的表達式求解。MAWPS是一個包含2373個問題的英語數據集,所有的問題都是一個未知變量的線性問題,可以用一個表達式來解決。
當然,最明顯的就是用的語言模型不同了。沈同學用的是預訓練模型BART,而OpenAI用的則是60億和1750億參數的GPT-3。