傳統上，只要參數的數量大于要滿足的方程數量，我們就可以使用參數化模型來進行數據插值。但在深度學習中，一個令人困惑的現象是，模型訓練使用的參數數量比這個經典理論所建議的要多得多。

深度學習中經常會出現各種大型的神經網絡，神經網絡是執行類人任務的領先 AI 系統。隨著它們參數的增多，神經網絡已經可以執行各種任務。按照數學的理論，神經網絡無需很大就能執行任務，例如在直線 y=2x 中，確定這條直線無需很多參數。但是，現代神經網絡的規模通常遠遠超出預測的要求，這種情況被稱為過度參數化。

在去年 12 月入選 NeurIPS 的一篇論文《A Universal Law of Robustness via Isoperimetry》中，來自微軟研究院的 Sébastien Bubeck 和斯坦福大學的 Mark Sellke 為神經網絡擴展成功背后的奧秘提供了新的解釋。他們表明，神經網絡必須比傳統預期規模要大得多，才能避免某些基本問題。這一發現為一個持續了幾十年的問題提供了一般性見解。

論文鏈接：https://arxiv.org/abs/2105.12806

Mark Sellke 和 Sébastien Bubeck 

瑞士洛桑聯邦理工學院的 Lenka Zdeborová 表示：他們的研究觸及了計算機科學的核心。神經網絡規模的標準來自對其如何記憶數據的分析。但要了解數據記憶，我們必須首先了解網絡的作用。

神經網絡中一項常見的任務是識別圖像中的目標。為了創建這種網絡，研究人員首先需要提供數據圖像及其標注，然后對其進行訓練以學習相關參數，之后模型能正確識別圖像中的目標。換句話說，訓練使網絡記住數據。更值得注意的是，一旦網絡記住了足夠多的訓練數據，它還能夠以不同程度的準確率預測它從未見過的目標，這一過程稱為泛化。

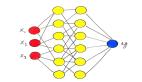
網絡的大小決定了它可以記住多少。這可以通過圖形來理解，想象一下，將兩個數據點放在 xy 平面上。你可以將這兩個點與由兩個參數描述的線連接起來。如果知道了這條線的一個點坐標以及一個原始數據點的 x 坐標，我們只需查看這條線（或使用參數）就可以計算出相應的 y 坐標。因為這條線已經記住了這兩個數據點。

神經網絡的原理與此類似。例如，圖像由成百上千個值描述 —— 每個像素是一個值。這些值在數學上等價于高維空間中一個點的坐標，坐標的數量稱為維度。

一個古老的數學結果表明，要將 n 個數據點與曲線擬合，則需要一個具有 n 個參數的函數。當神經網絡在 1980 年代首次作為一種有影響的力量出現時，研究者的想法與此相同，他們認為對于神經網絡來說，應該只需要 n 個參數來擬合 n 個數據點 —— 無論數據的維度如何。

德克薩斯大學奧斯汀分校的 Alex Dimakis 表示：「現在的研究改變了，我們經常創建參數數量超過訓練樣本數量的神經網絡。這意味著相關研究文獻書籍必須重寫。」

Bubeck 和 Sellke 并沒有打算重寫任何東西。他們正在研究神經網絡缺乏的另一種特性，稱為穩健性（robustness），即網絡處理微小變化的能力。例如，一個穩健性較差的網絡可能已經學會了識別長頸鹿，但它會將一個幾乎沒有修改過的圖片錯誤地標記為沙鼠，這就是網絡穩健性帶來的影響。 

2019 年，當 Bubeck 及其同事意識到該問題與網絡規模有關時，他們正在尋求證明有關該問題的定理。新研究表明過度參數化對于網絡的穩健性是必要的。他們通過將數據點與曲線擬合所需的參數來做到這一點，該曲線具有與穩健性等效的數學屬性：平滑度。

為了看到這一點，再次想象平面中的一條曲線，其中 x 坐標代表單個像素的顏色，y 坐標代表圖像標簽。由于曲線是平滑的，如果你稍微修改像素的顏色，沿著曲線移動一小段距離，相應的預測只會發生很小的變化。另一方面，對于極度鋸齒狀的曲線，x 坐標（顏色）的微小變化會導致 y 坐標（圖像標簽）發生劇烈變化，原本識別為長頸鹿的圖像可以變成沙鼠。

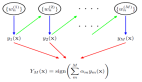
Bubeck 和 Sellke 的研究表明，平滑擬合高維數據點不僅需要 n 個參數，還需要 n × d 個參數，其中 d 是輸入的維度（例如，784 表示 784 像素的圖像）。換句話說，如果你想讓神經網絡穩健地記住它的訓練數據，過度參數化不僅有幫助 —— 而是絕對有效。證明依賴于一個關于高維幾何的奇特事實 —— 即放置在球體表面上的隨機分布的點，幾乎都彼此相距一個完整的直徑。點與點之間的大間隔意味著用一條平滑曲線擬合它們需要許多額外的參數。

耶魯大學的 Amin Karbasi 表示，「這個證明非常基礎 —— 不需要繁重的數學運算，它說明了一些非常普遍的東西。」

該結果提供了一種新方法來理解為什么擴大神經網絡規模的簡單策略如此有效。與此同時，其他研究揭示了過度參數化帶來幫助的更多原因，例如它可以提高訓練過程的效率，以及網絡的泛化能力。

雖然我們現在知道過度參數化對于穩健性是必要的，但尚不清楚穩健性對其他事物的必要性。通過將其與過度參數化聯系起來，新的證據似乎表明穩健性可能比想象的更加重要，是一個可以帶來許多好處的關鍵因素。

「穩健性似乎是泛化的先決條件，」Bubeck 說到。「如果你有一個系統，你只是稍微擾亂它，然后它就失控了，這會是怎樣的系統？這是不可接受的，這是一個非常基礎和基本的要求。」