1996年的8月19日至23日，芬蘭的瓦薩舉行了由芬蘭人工智能協(xié)會和瓦薩大學組織的芬蘭人工智能會議。

會議上發(fā)表的一篇論文證明：圖靈機就是一個循環(huán)神經(jīng)網(wǎng)絡。

沒錯，這是在26年前！

讓我們來看一看，這篇發(fā)表于1996年的論文。

1 前言

1.1 神經(jīng)網(wǎng)絡分類

神經(jīng)網(wǎng)絡可用于分類任務，判斷輸入模式是否屬于特定的類別。

長期以來，人們都知道單層前饋網(wǎng)絡只能用于對線性可分的模式進行分類，即連續(xù)層越多，類的分布就越復雜。

當在網(wǎng)絡結(jié)構中引入反饋時，感知器輸出值被循環(huán)利用，連續(xù)層的數(shù)量原則上變?yōu)闊o限大。

算力有沒有質(zhì)的提升？答案是肯定的。

例如，可以構造一個分類器來判斷輸入整數(shù)是否為素數(shù)。

事實證明，用于此目的的網(wǎng)絡大小可以是有限的，即使輸入整數(shù)大小不受限制，可以正確分類的素數(shù)數(shù)量也是無限的。

在本文中，「由相同計算元素組成的循環(huán)網(wǎng)絡結(jié)構」可用于完成任何（算法上的）可計算功能。

1.2 關于可計算性

根據(jù)可計算性理論的基本公理，可以使用圖靈機實現(xiàn)可計算函數(shù)，有多種方法可以實現(xiàn)圖靈機。

定義程序語言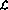。該語言有四種基本操作：

這里，V代表任何具有正整數(shù)值的變量，j代表任何行號。

可以證明，如果一個函數(shù)是圖靈可計算的，則可以使用這種簡單的語言對其進行編碼（有關詳細信息，請參見[1]）。

2 圖靈網(wǎng)絡

2.1 遞歸神經(jīng)網(wǎng)絡結(jié)構

本文研究的神經(jīng)網(wǎng)絡由感知器組成，它們都具有相同的結(jié)構，感知器數(shù)q的運算可以定義為

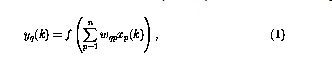
其中，當前時刻的感知器輸出（用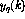表示）是使用n輸入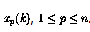計算的。

非線性函數(shù)f現(xiàn)在可定義為

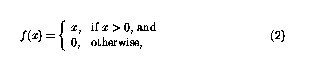
這樣函數(shù)就可以簡單地「切斷」負值，感知器網(wǎng)絡中的循環(huán)意味著感知器可以以復雜的方式組合。

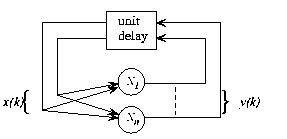
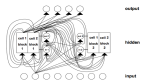
圖1 遞歸神經(jīng)網(wǎng)絡的整體框架，結(jié)構自主無外部輸入，網(wǎng)絡行為完全由初始狀態(tài)決定

在圖1中，遞歸結(jié)構顯示在一個通用框架中：現(xiàn)在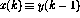和n是感知器的數(shù)量，從感知器p到感知器q的連接由（1）中的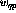標量權重表示。

即給定初始狀態(tài)，網(wǎng)絡狀態(tài)會迭代到不再發(fā)生變化，結(jié)果可以在該穩(wěn)定狀態(tài)或網(wǎng)絡的「固定點」下讀取。

2.2 神經(jīng)網(wǎng)絡建構

接下來闡述該程序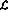如何在感知器網(wǎng)絡中實現(xiàn)。該網(wǎng)絡由以下節(jié)點（或感知器）組成：

• 對于程序中的每個變量V，都有一個變量節(jié)點。
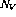• 對于每個程序行i，都有一個指令節(jié)點。
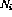• 對于第i行上的每個條件分支指令，另外還有兩個轉(zhuǎn)移節(jié)點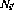和。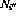

語言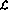程序的實現(xiàn)包括感知器網(wǎng)絡的以下變化：

• 對于程序中的每個變V，使用以下鏈接擴充網(wǎng)絡：

• 如果程序代碼的第i行沒有操作(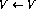)，則使用以下鏈接擴充網(wǎng)絡（假設該節(jié)點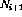存在：

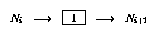
• 如果第i行有增量操作(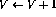)，則按如下方式擴充網(wǎng)絡：

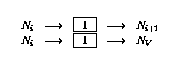
• 如果第i行有遞減操作(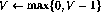)，則按如下方式擴充網(wǎng)絡：

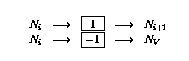
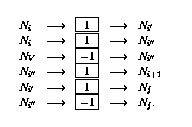
• 如果第i行有條件分支(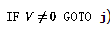)，則按如下方式擴充網(wǎng)絡：

2.3 等效性證明

現(xiàn)在需要證明的是，「網(wǎng)絡的內(nèi)部狀態(tài)或網(wǎng)絡節(jié)點的內(nèi)容」，可以用程序狀態(tài)來標識，同時網(wǎng)絡狀態(tài)的連續(xù)性與程序流對應。

定義網(wǎng)絡的「合法狀態(tài)」如下：

• 至所有轉(zhuǎn)換節(jié)點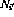和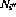（如2.2中所定義）的輸出為零()；
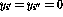• 至多一個指令節(jié)點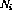有單位輸出(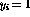)，所有其他指令節(jié)點有零輸出，并且
• 變量節(jié)點具有非負整數(shù)輸出值。

如果所有指令節(jié)點的輸出均為零，則狀態(tài)最終狀態(tài)。一個合法的網(wǎng)絡狀態(tài)可以直接解釋為一個程序「快照」——如果?，程序計數(shù)器在第i行，相應的變量值存儲在變量節(jié)點中。

網(wǎng)絡狀態(tài)的變化是由非零節(jié)點激活的。

首先，關注變量節(jié)點，事實證明它們表現(xiàn)為積分器，節(jié)點的先前內(nèi)容被循環(huán)回同一節(jié)點。

從變量節(jié)點到其他節(jié)點的唯一連接具有負權重——這就是為什么包含零的節(jié)點不會改變，因為非線性的原因（2）。

接下來，詳細說明指令節(jié)點。假設唯一的非零指令節(jié)點?在時間k---這對應于程序計數(shù)器在程序代碼中第i行。

若程序中第i行是?，則網(wǎng)絡向前一步的行為可表示為（只顯示受影響的節(jié)點）

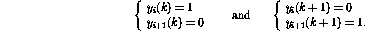
事實證明，新的網(wǎng)絡狀態(tài)再次合法。與程序代碼相比，這對應于程序計數(shù)器被轉(zhuǎn)移到第i+1行。

另一方面，如果程序中的第i行是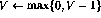，則向前一步的行為是

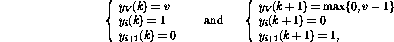
這樣，除了將程序計數(shù)器轉(zhuǎn)移到下一行之外，變量V的值也會遞減。如果第i行是

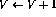，網(wǎng)絡的操作將是相同的，除了變量V的值增加。

第i行的條件分支操作（IF 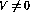 GOTO j）激活更復雜的操作序列：

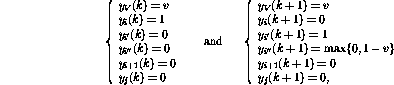
最后，

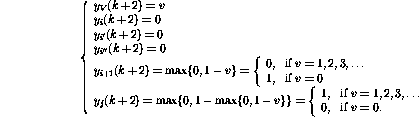
事實證明，在這些步驟之后，網(wǎng)絡狀態(tài)可以再次被解釋為另一個程序快照。

變量值已更改，token已轉(zhuǎn)移到新位置，就像執(zhí)行了相應的程序行一樣。

如果token消失，網(wǎng)絡狀態(tài)不再改變——這只有在程序計數(shù)器「超出」程序代碼時才會發(fā)生，這意味著程序終止。

網(wǎng)絡的運行也類似對應程序的運行，證明完成。

3 修改

3.1 擴展

定義額外的流線型指令很容易，這些指令可以使編程更容易，并且生成的程序更具可讀性和執(zhí)行速度。例如，

• 第i行的無條件分支（GOTO j）可以實現(xiàn)為
  ?
• 將常量c添加到第i行的變量（?）可以實現(xiàn)為
  ?
• 行i上的另一種條件分支（IF V=0 GOTO j ）可以實現(xiàn)為
  ?
• 此外，可以同時評估各種遞增/遞減指令。假設要執(zhí)行以下操作：?。只需要一個節(jié)點?：
  ?

上述方式絕不是實現(xiàn)圖靈機的唯一途徑。

這是一個簡單的實現(xiàn)，在應用程序中不一定是最佳的。

3.2 矩陣制定

上述構造也可以以矩陣的形式實現(xiàn)。

基本思想是將變量值和「程序計數(shù)器」存儲在進程狀態(tài)s中，并讓狀態(tài)轉(zhuǎn)換矩陣A代表節(jié)點之間的鏈接。

矩陣結(jié)構的運算可以定義為一個離散時間的動態(tài)過程

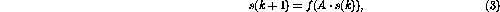
其中非線性向量值函數(shù)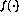現(xiàn)在按元素定義，如（2）中所示。

狀態(tài)轉(zhuǎn)移矩陣A的內(nèi)容很容易從網(wǎng)絡公式中解碼出來——矩陣元素是節(jié)點之間的權重。

該矩陣公式類似于[3]中提出的「概念矩陣」框架。

4 例子

假設要實現(xiàn)一個簡單的函數(shù)y=x，也就是說，輸入變量x的值應該傳遞給輸出變量y。使用語言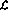可以將其編碼為（讓「入口點」現(xiàn)在不是第一行而是第三行）：

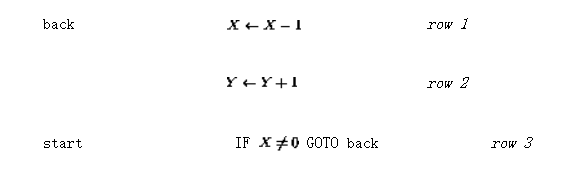
生成的感知器網(wǎng)絡如圖2所示。

實線代表正連接（權重為1），虛線代表負連接（權重-1）。與圖1相比，重新繪制了網(wǎng)絡結(jié)構，并通過在節(jié)點中集成延遲元件來簡化網(wǎng)絡結(jié)構。

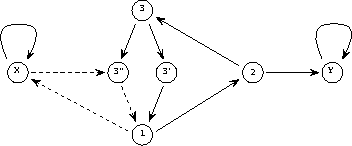
圖2 簡單程序的網(wǎng)絡實現(xiàn)

在矩陣形式中，上面的程序看起來像

矩陣A中的前兩行/列對應于連接到代表兩個變量Y和X的節(jié)點的鏈接，接下來的三行代表三個程序行（1、2和3），最后兩個代表分支指令所需的附加節(jié)點（3'和3''）。

然后是初始（迭代前）和最終（迭代后，找到固定點時）的狀態(tài)

如果變量節(jié)點的值將嚴格保在0和1之間，則動態(tài)系統(tǒng)（3）的操作將是線性的，該函數(shù)?根本沒有影響。

原則上，然后可以在分析中使用線性系統(tǒng)理論。

例如，在圖3中，示出了狀態(tài)轉(zhuǎn)移矩陣A的特征值。

即使在上面的例子中單位圓外有特征值，非線性使得迭代總是穩(wěn)定的。

事實證明，迭代總是在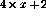步驟之后收斂，其中。

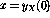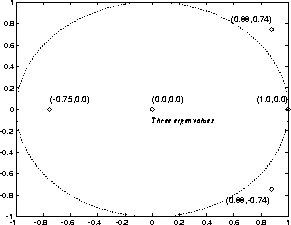
圖3 簡單程序的「特征值」

5 討論

5.1 理論方面

結(jié)果表明，圖靈機可以編碼為感知器網(wǎng)絡。

根據(jù)定義，所有可計算函數(shù)都是圖靈可計算的——在可計算性理論的框架內(nèi)，不存在更強大的計算系統(tǒng)。

這就是為什么，可以得出結(jié)論——

循環(huán)感知器網(wǎng)絡（如上所示）是圖靈機的（又一種）形式。

這種等價的好處是可計算性理論的結(jié)果很容易獲得——例如，給定一個網(wǎng)絡和一個初始狀態(tài)，就不可能判斷這個過程最終是否會停止。

上述理論等價性并沒有說明計算效率的任何信息。

與傳統(tǒng)的圖靈機實現(xiàn)（實際上是今天的計算機）相比，網(wǎng)絡中發(fā)生的不同機制可以使一些功能在這個框架中更好地實現(xiàn)。

 至少在某些情況下，例如，一個算法的網(wǎng)絡實現(xiàn)可以通過允許snapshot向量中的多個「程序計數(shù)器」來被并行化。

網(wǎng)絡的運行是嚴格本地的，而不是全局的。

一個有趣的問題出現(xiàn)了，例如，是否可以在網(wǎng)絡環(huán)境中更有效地攻擊NP完全問題！

與語言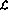相比，網(wǎng)絡實現(xiàn)具有以下「擴展」：

• 變量可以是連續(xù)的，而不僅僅是整數(shù)值。實際上，呈現(xiàn)實數(shù)的（理論）能力使網(wǎng)絡實現(xiàn)比語言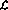更強大，所有以語言呈現(xiàn)的數(shù)字都是有理數(shù)。
• 可以同時存在各種「程序計數(shù)器」，并且控制的轉(zhuǎn)移可能是「模糊的」，這意味著指令節(jié)點提供的程序計數(shù)器值可能是非整數(shù)。
• 一個較小的擴展是可自由定義的程序入口點。這可能有助于簡化程序——例如，變量的復制在上面的三個程序行中完成，而名義解決方案（參見[1]）需要七行和一個額外的局部變量。

與原始程序代碼相比，矩陣公式顯然是比程序代碼更「連續(xù)」的信息表示形式——可以（經(jīng)常）修改參數(shù)，而迭代結(jié)果不會突然改變。

這種「冗余」也許可以在某些應用中使用。

例如，當使用遺傳算法（GA）進行結(jié)構優(yōu)化時，可以使遺傳算法中使用的隨機搜索策略更加高效：在系統(tǒng)結(jié)構發(fā)生變化后，可以搜索連續(xù)成本函數(shù)的局部最小值使用一些傳統(tǒng)技術（參見[4]）。

通過示例學習有限狀態(tài)機結(jié)構，如[5]中所述，可以知道：在這種更復雜的情況下也采用迭代增強網(wǎng)絡結(jié)構的方法。

不僅神經(jīng)網(wǎng)絡理論可能受益于上述結(jié)果——僅看動態(tài)系統(tǒng)公式（3），很明顯，在可計算性理論領域發(fā)現(xiàn)的所有現(xiàn)象也都以簡單的形式存在——尋找非線性動態(tài)過程。

例如，停機問題的不可判定性是系統(tǒng)論領域的一個有趣貢獻：對于任何表示為圖靈機的決策過程，都存在形式（3）的動態(tài)系統(tǒng)，它違背了這個過程——對于例如，無法構建通用的穩(wěn)定性分析算法。

5.2 相關工作

所呈現(xiàn)的網(wǎng)絡結(jié)構與遞歸來Hopfield神經(jīng)網(wǎng)絡范式之間存在一些相似之處（例如，參見[2]）。

在這兩種情況下，「輸入」都被編碼為網(wǎng)絡中的初始狀態(tài)，「輸出」在迭代后從網(wǎng)絡的最終狀態(tài)中讀取。

Hopfield網(wǎng)絡的固定點是預編程的模式模型，輸入是「噪聲」模式——該網(wǎng)絡可用于增強損壞的模式。

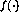中非線性函數(shù)的展望（2）使得上述「圖靈網(wǎng)絡」中可能的狀態(tài)數(shù)量是無限的。

與單元輸出始終為-1或1的Hopfield網(wǎng)絡相比，可以看出，理論上，這些網(wǎng)絡結(jié)構有很大不同。

例如，雖然Hopfield網(wǎng)絡中的穩(wěn)定點集是有限的，但以圖靈網(wǎng)絡為代表的程序通常具有無限數(shù)量的可能結(jié)果。

Hopfield網(wǎng)絡的計算能力在[6]中進行了討論。

Petri網(wǎng)是基于事件和并發(fā)系統(tǒng)建模的強大工具[7]。

Petri網(wǎng)由位和轉(zhuǎn)移以及連接它們的弧組成。每個地方可能包含任意數(shù)量的token，token的分布稱為Petri網(wǎng)的標記。

如果轉(zhuǎn)換的所有輸入位置都被標記占用，則轉(zhuǎn)換可能會觸發(fā)，從每個輸入位置刪除一個標記，并向其每個輸出位置添加一個標記。

可以證明，具有附加抑制弧的擴展Petri網(wǎng)也具有圖靈機的能力（參見[7]）。

上述圖靈網(wǎng)與Petri網(wǎng)的主要區(qū)別在于Petri網(wǎng)的框架更為復雜，具有專門定制的結(jié)構，不能用簡單的一般形式（3）來表達。

參考

1 Davis, M. and Weyuker, E.: Computability, Complexity, and Languages---Fundamentals of Theoretical Computer Science. Academic Press, New York, 1983.

2 Haykin, S.: Neural Networks. A Comprehensive Foundation. Macmillan College Publishing, New York, 1994.

3 Hy?tyniemi, H.: Correlations---Building Blocks of Intelligence? In ?lyn ulottuvuudet ja oppihistoria (History and dimensions of intelligence), Finnish Artificial Intelligence Society, 1995, pp. 199--226.

4 Hy?tyniemi, H. and Koivo, H.: Genes, Codes, and Dynamic Systems. In Proceedings of the Second Nordic Workshop on Genetic Algorithms (NWGA'96), Vaasa, Finland, August 19--23, 1996.

5 Manolios, P. and Fanelli, R.: First-Order Recurrent Neural Networks and Deterministic Finite State Automata. Neural Computation 6, 1994, pp. 1155--1173.

6 Orponen, P.: The Computational Power of Discrete Hopfield Nets with Hidden Units. Neural Computation 8, 1996, pp. 403--415.

7 Peterson, J.L.: Petri Net Theory and the Modeling of Systems. Prentice--Hall, Englewood Cliffs, New Jersey, 1981.

參考資料：

??http://users.ics.aalto.fi/tho/stes/step96/hyotyniemi1/???