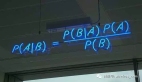Alex Graves新作貝葉斯流網絡,解決離散數據生成問題,滿論文都是數學公式
近來,大規模神經網絡徹底改變了生成式模型,使模型具有前所未有的捕捉許多變量之間復雜關系的能力,例如建立高分辨率圖像中所有像素的聯合模型。
大多數神經網絡(包括自回歸模型、基于流的模型、深度 VAE 和擴散模型)表達能力的關鍵在于,它們編碼的聯合分布被分解為一系列步驟,從而避免了「維數災難(curse of dimensionality)」。也就是說,它們將難題分解成多個簡單問題來解決。
自回歸網絡目前是語言建模領域的 SOTA 方法,并且通常在自然排序的離散數據上表現良好。然而,事實證明自回歸網絡在圖像生成等領域效果較差,因為這些領域的數據是連續的,并且變量之間不存在自然順序。自回歸模型還有一個缺點是,生成樣本需要與數據中變量一樣多的網絡更新。擴散模型是一種應用于圖像生成的有效替代框架,但傳輸過程會變得更加復雜。
然而,當數據是離散的,擴散模型的性能仍不及自回歸模型。最近,機器學習領域知名研究者、神經圖靈機(NTM)提出者和可微神經計算機的創造者之一 Alex Graves 以第一作者的身份發表了一篇新論文,提出了一種新型生成模型 —— 貝葉斯流網絡(Bayesian Flow Networks,BFN)。與擴散模型不同的是,BFN 對數據分布的參數進行操作,而不是對數據本身的噪聲版本進行操作。這確保了生成過程是完全連續且可微的,即使數據是離散的。

論文地址:https://arxiv.org/abs/2308.07037

論文一作 Alex Graves,他是圖靈獎得主 Geoffrey Hinton 的學生。
BFN 方法會根據噪聲數據樣本使用貝葉斯推斷修改一組獨立分布的參數,然后將其作為輸入傳遞給神經網絡,該神經網絡會輸出一個相互依賴的分布,然后從簡單的先驗開始并迭代更新上述兩個分布,產生一種類似于擴散模型逆過程的生成過程,但 BFN 在概念上更簡單,因為不需要前向過程。
BFN 的整體概覽如下圖 1 所示。在每一步中,消息發送者(Sender)Alice 都會向消息接收者(Receiver)Bob 發送一條消息,包含關于數據的一些信息。
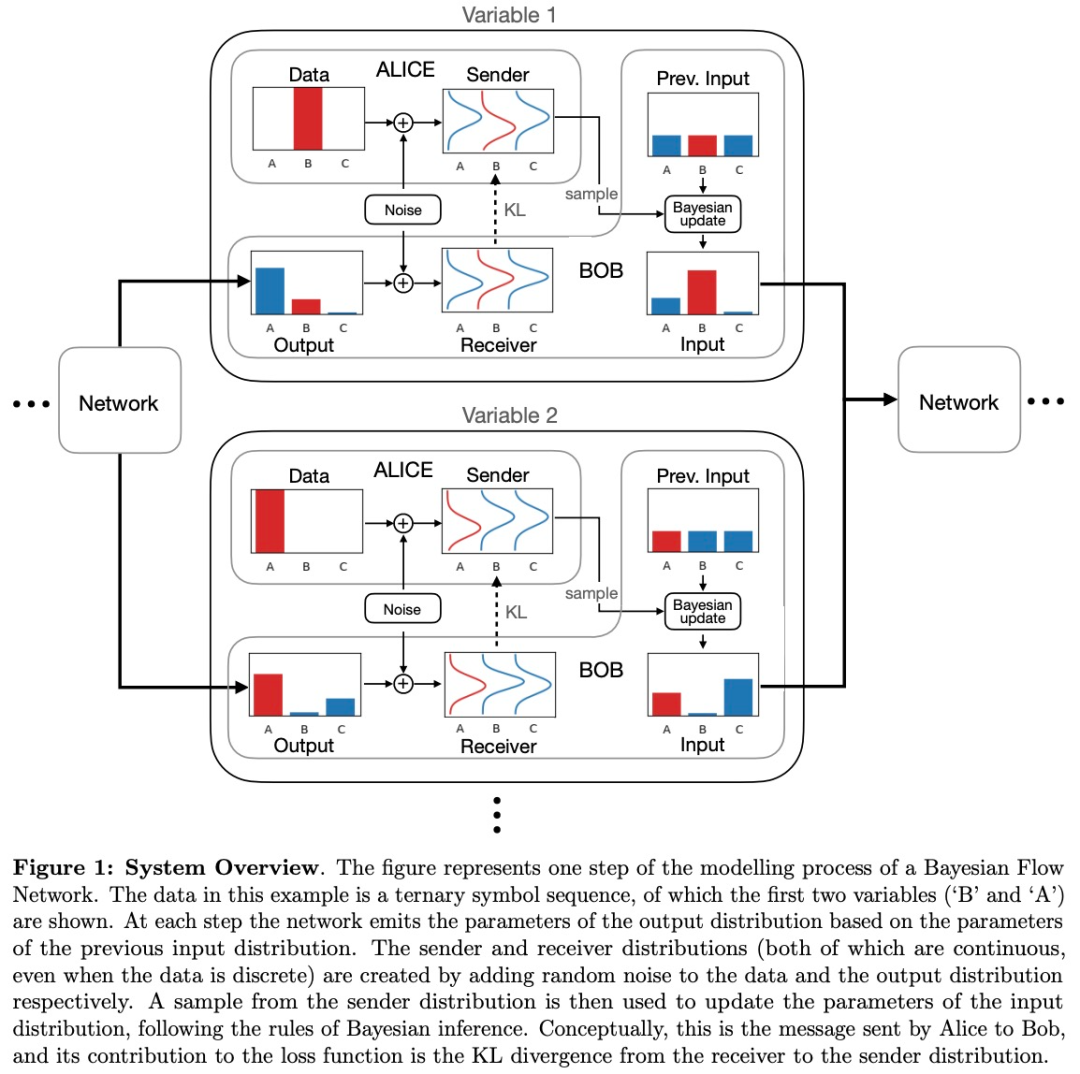
其中,Bob 會嘗試猜測消息是什么:他猜測得越好,傳輸消息所需的比特數就越少。收到消息后,Bob 使用剛剛獲得的信息來改進對下一條消息的猜測。
重復該過程,每一步的預測都會得到改進。傳輸成本之和是完整文本序列的負對數概率,通過最大似然訓練進行損失函數最小化。這也是 Alice 使用算術編碼將片段傳輸給 Bob 所需的最小位數。因此,用最大似然擬合自回歸模型與訓練數據壓縮之間存在直接的對應關系。
上述傳輸過程定義了一個 n 步損失函數,通過將 n 擴展到∞,就能推廣到連續時間。連續時間損失函數在數學上比離散時間損失函數更簡單、易于計算。經過連續時間損失訓練的 BFN 可以在推斷和采樣期間運行任意數量的離散步驟,并且性能隨著步驟數量的增加而提升。
總的來說,BFN 結合了貝葉斯推斷和深度學習的優勢,前者為單個變量提供了一種極佳的數學方法,后者則擅長整合多個相關變量的信息。
LSTM 提出者和奠基者 Sepp Hochreiter 表示:「貝葉斯流網絡 (BFN) 作為擴散模型的替代者,它更新的兩個分布過程可看作是一個生成過程,就像沒有前向傳遞的擴散模型一樣。實驗顯示,在 text8 字符級語言建模上優于離散擴散。」
論文作者之一 Rupesh Kumar Srivastava 表示,「這項研究使得我們可以通過選擇合適的分布,輕松地將 BFN 框架適應于連續和離散數據,并且在 MNIST、CIFAR-10 和 text8 任務上得到了很好的結果。」
貝葉斯流網絡
接下來我們介紹一下貝葉斯流網絡(Bayesian Flow Networks,BFN)的基本數學形式。本節都是公式推導,大家可以參考原論文了解更詳細的信息。
輸入分布和 Sender 分布:給定 D 維數據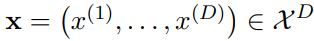 ,
,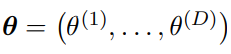 為因式輸入分布
為因式輸入分布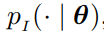 的參數,則輸入分布公式如下:
的參數,則輸入分布公式如下:
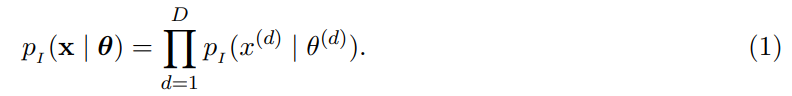
經過一系列變換后,得到 Sender 分布公式:
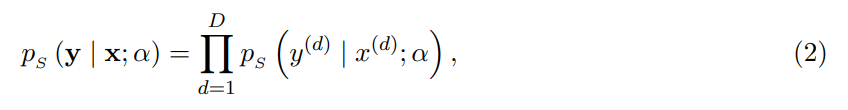
輸出分布數據傳輸過程中,輸入參數 θ 與過程時間 t 一起作為輸入傳遞給神經網絡 Ψ,然后網絡輸出一個向量,得到輸出分布:
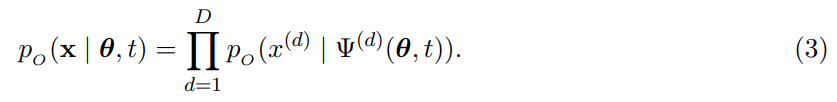
與輸入分布不同,輸出分布可以利用上下文信息,例如圖像中的周圍像素或文本中的相關單詞。
Receiver 分布給定 Sender 分布和輸出分布, Receiver 分布可以表述為:
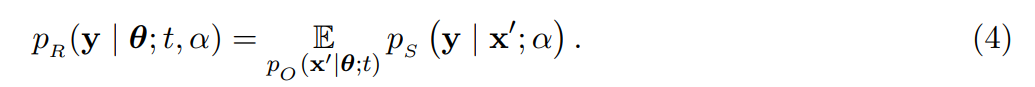
由上式可得,Receiver 分布有兩個不確定來源,即 Sender 分布和輸出分布。
貝葉斯更新
對于給定的參數 θ,參數更新的方式如下所示,其中 y 為 Sender 樣本, α 為準確率:

得到貝葉斯更新分布:
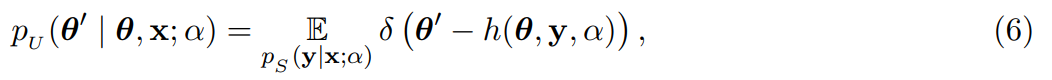
本文認為,從某種意義上講,準確率 α 是可以相加的,從而得到總的貝葉斯更新分布公式:
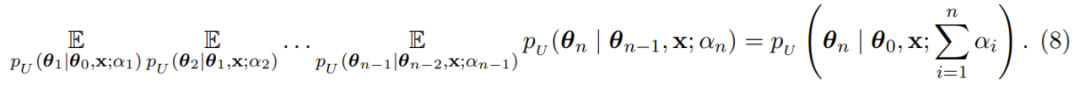
通過執行無限多的傳輸步驟,貝葉斯更新過程可以推廣到連續時間。假設 t ∈ [0, 1] 為處理時間,α(t) > 0 為時間 t 的準確率,得到準確率時間表:

貝葉斯流分布
給定先驗參數 θ_0、貝葉斯更新分布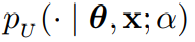 以及準確率時間表 β(t), 貝葉斯流分布可以表示為
以及準確率時間表 β(t), 貝葉斯流分布可以表示為
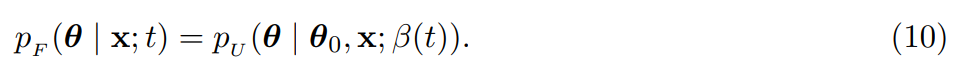
損失函數
損失函數定義為如下方式:

其中,
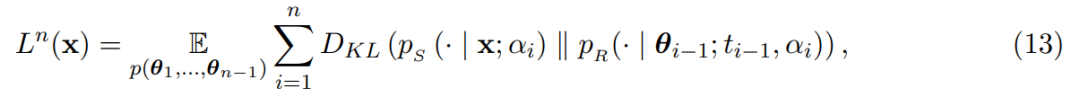
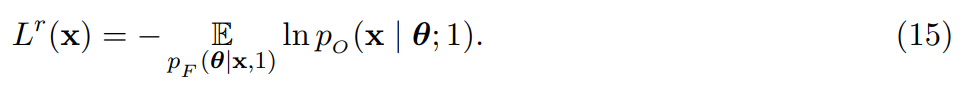
L (x) 可以推導為變分自編碼器(VAE)的損失函數,經過一系列變化,損失函數表述為:
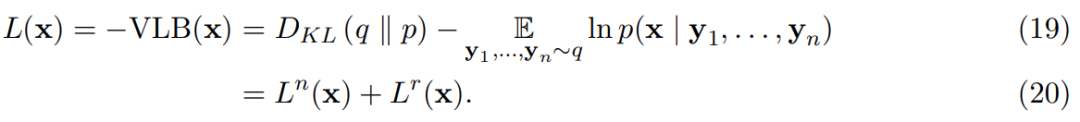
根據損失函數(16),該研究又推導出了離散損失:
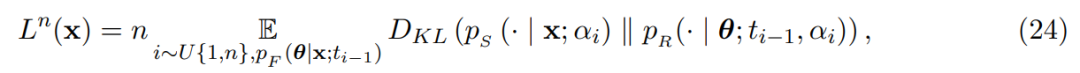
以及連續時間損失:
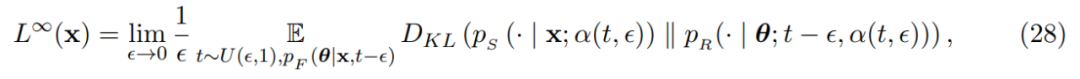
實驗
該研究在以下生成基準上評估了 BFN 網絡,包括 CIFAR-10(32×32 8 位彩色圖像)、動態二值化 MNIST(28×28 手寫數字的二值化圖像)以及 text8(長度 256 個字符序列,大小為 27 個字母)。
動態二值化 MNIST
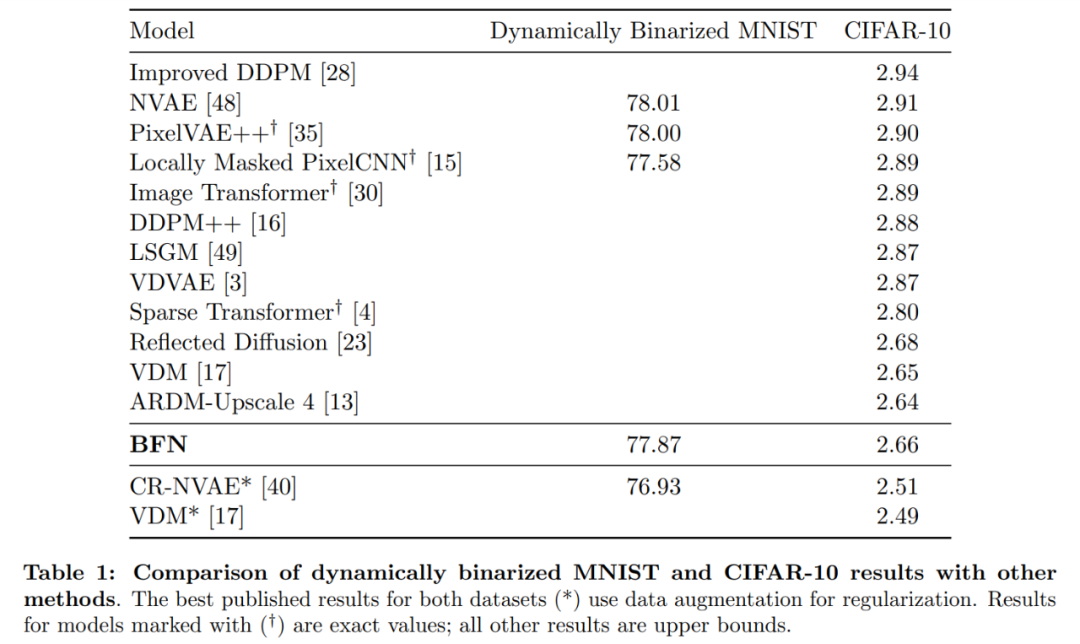
從表 1 可以看出,BFN 在沒有數據增強的情況下達到該任務最好的性能。
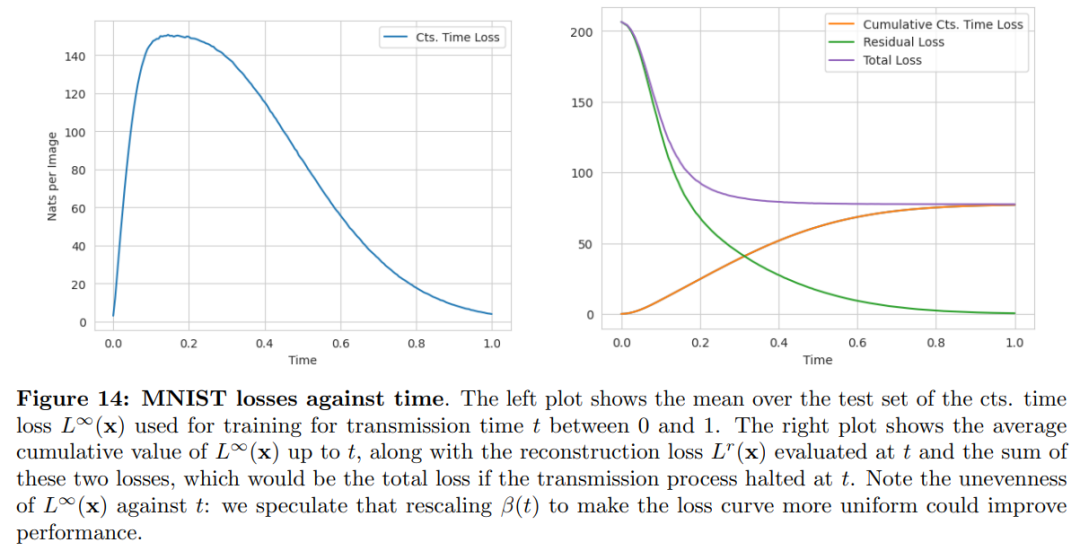
下圖為 MNIST 損失曲線:表明對于二進制數據,準確率時間表不是最優的。
CIFAR-10
該研究在 CIFAR-10 上進行了兩組生成建模實驗,一組 bit-depth 為 8 ,對應于顏色通道有 256 個離散 bin,另一組 bit-depth 為 4 ,對應于顏色通道為 16 個 bin。
表 3 顯示,對于 16 bins,離散損失比連續損失提供了更好的性能,并且訓練時間也快得多。這一結果對應了這樣一個假設,即 bin 相對較低時,使用離散損失進行訓練是最有益的。此外,對于 16 和 256 個 bin,當步數 n 較低(例如 10 或 25)時,離散訓練會給出更好的結果。然而,在 256 個 bin 上,連續損失比離散損失具有更好的性能。
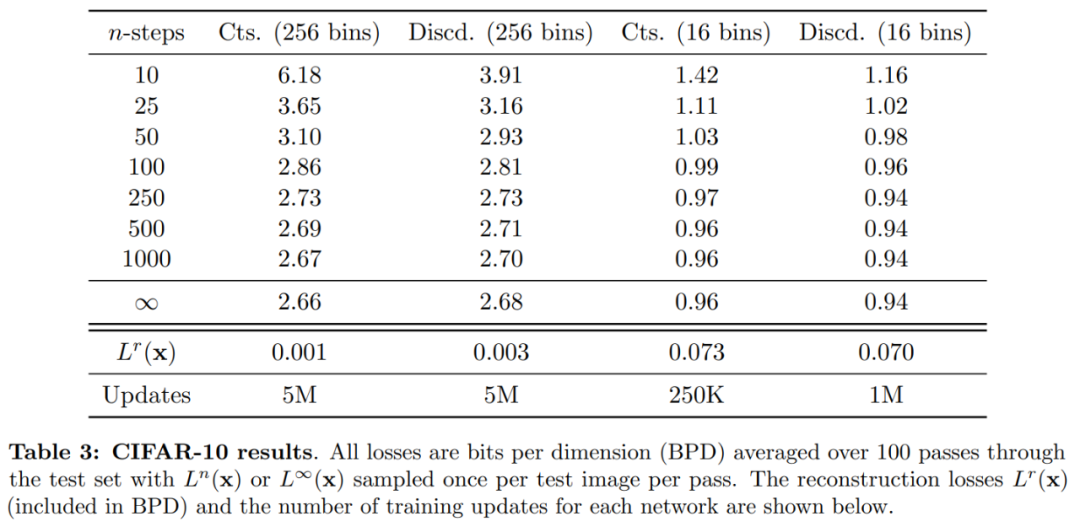
圖 15 顯示,使用 16 個 bin 進行離散訓練比使用 256 個 bin 進行離散訓練可提供更好的樣本質量。

TEXT8
表 4 顯示,BFN 在 text8 測試集上產生了 1.41 BPC,這比其他文獻中發現的所有離散擴散模型都要好,并且接近最佳模型 MAC(1.40 BPC)。
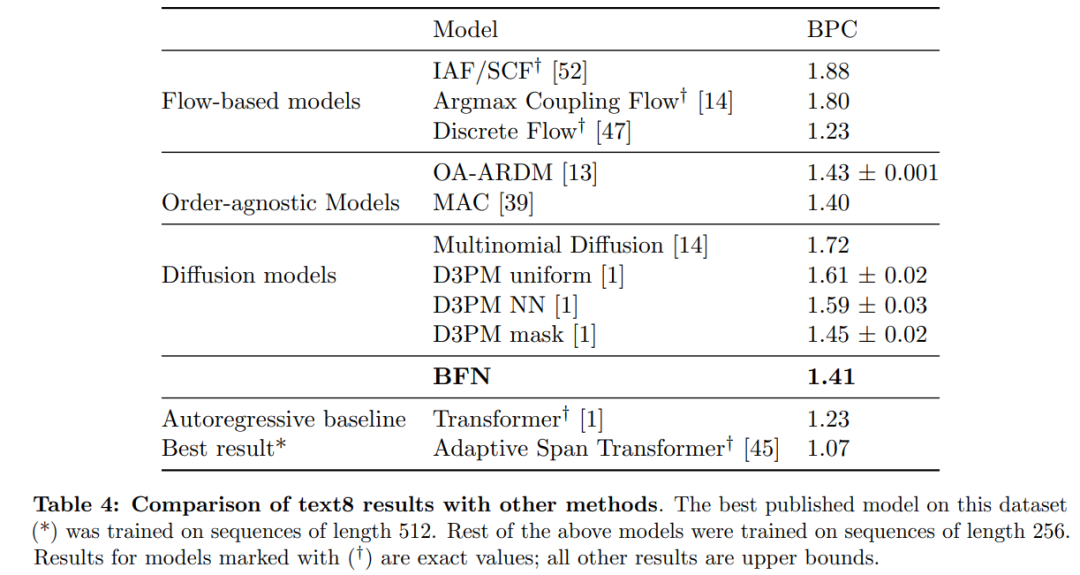
表 5 顯示,對于步數 n 的減少,BFN 的性能還是相當穩健的,只需 100 步即可達到 1.43 BPC。通過離散時間損失訓練可能會改善這個結果。