在本系列的 第一篇文章 中，我們討論了人工智能、機器學習、深度學習、數據科學等領域的關聯和區別。我們還就整個系列將使用的編程語言、工具等做出了一些艱難的選擇。最后，我們還介紹了一點矩陣的知識。在本文中，我們將深入地討論人工智能的核心——矩陣。不過在此之前，我們先來了解一下人工智能的歷史。

我們為什么需要了解人工智能的歷史呢？歷史上曾出現過多次人工智能熱潮，但在很多情況下，對人工智能潛力的巨大期望都未能達成。了解人工智能的歷史，有助于讓我們看清這次人工智浪潮是會創造奇跡，抑或只是另一個即將破滅的泡沫。

我們對人工智能的最尋起源于何時呢？是在發明數字計算機之后嗎？還是更早呢？我相信對一個無所不知的存在的追求可以追溯到文明之初。比如古希臘神話中的 德爾菲Delphi 就是這樣一位能回答任何問題的先知。從遠古時代起，對于超越人類智慧的創造性機器的探索同樣吸引著我們 。歷史上有過幾次制造國際象棋機器的失敗的嘗試。其中就有臭名昭著的機械特克Mechanical Turk，它并不是真正的機器人，而是由一位藏在內部的棋手操控的。約翰·納皮爾John Napier 發明的對數、布萊斯·帕斯卡Blaise Pascal 的計算器、查爾斯·巴貝奇Charles Babbage 的差分機等，這些都是人工智能研究的前身。回顧人類歷史，你會發現更多真實或虛構的時刻，人們想要獲得超越人腦的智能。如果不考慮以上這些歷史成就，對真正人工智能的探索起始于數字計算機的發明。

那么，人工智能發展至今有哪些里程碑呢？前面已經提到，數字計算機的發明是人工智能研究歷程中最重要的事件。與可擴展性依賴于功率需求的機電設備不同，數字設備受益于技術進步，比如從真空管到晶體管到集成電路再到如今的超大規模集成技術。

人工智能發展的另一個里程碑是 阿蘭·圖靈Alan Turing 首次對人工智能的理論分析。他提出的 圖靈測試Turing test 是最早的人工智能測試方法之一。現在圖靈測試可能已經不太適用了，但它是定義人工智能的最初嘗試之一。圖靈測試可以簡單描述如下：假設有一臺能夠與人類對話的機器，如果它能在對話中讓人無法分辨它是人還是機器，那么就可以認為這臺機器具有智能。如今的聊天機器人非常強大，使我們很容易看出圖靈測試無法識別出真正的人工智能。但在 20 世紀 50 年代初，這確實為理解人工智能提供了一個理論框架。

20 世紀 50 年代末，約翰·麥卡錫John McCarthy 發明了 Lisp 編程語言。它是最早的高級編程語言之一。在此之前，計算機編程用的是機器語言和匯編語言（眾所周知地難用）。有了強大的機器和編程語言，計算機科學家中的樂觀主義和夢想家順理成章地開始用它們來創造人工智能。20 世紀 60 年代初，對人工智能機器的期望達到了頂峰。當然計算機科學領域取得了很大發展，但人工智能的奇跡發生了嗎？很遺憾，并沒有。20 世紀 60 年代見證了第一次人工智能熱潮的興起和破滅。然而計算機科學以無與倫比的速度繼續發展著。

到了 70 年代和 80 年代，算法在這一時期發揮了主要作用。在這段時間，許多新的高效算法被提出。20 世紀 60 年代末高德納·克努特Donald Knuth（我強烈建議你了解一下他，在計算機科學界，他相當于數學界的高斯或歐拉）著名的《計算機程序設計藝術The Art of Computer Programming》第一卷的出版標志著算法時代的開始。在這些年中，開發了許多通用算法和圖算法。此外，基于人工神經網絡的編程也在此時興起。盡管早在 20 世紀 40 年代，沃倫·S.·麥卡洛克Warren S. McCulloch和沃爾特·皮茨Walter Pitts 就率先提出了人工神經網絡，但直到幾十年后它才成為主流技術。今天，深度學習幾乎完全是基于人工神經網絡的。算法領域的這種發展導致了 20 世紀 80 年代人工智能研究的復蘇。然而，這一次，通信和算力的限制阻礙了人工智能的發展，使其未能達到人們野心勃勃的預期。然后是 90 年代、千禧年，直到今天。又一次，我們對人工智能的積極影響充滿了熱情和希望。

我你們可以看到，在數字時代，人工智能至少有兩次前景光明的機會。但這兩次人工智能都沒有達到它的預期。現在的人工智能浪潮也與此類似嗎？當然這個問題很難回答。但我個人認為，這一次人工智能將產生巨大的影響（LCTT 譯注：本文發表于 2022 年 6 月，半年后，ChatGTP 才推出）。是什么讓我做出這樣的預測呢？第一，現在的高性能計算設備價格低廉且容易獲得。在 20 世紀 60 年代或 80 年代，只有幾臺如此強大的計算設備，而現在我們有數百萬甚至數十億臺這樣的機器。第二，現在有大量數據可用來訓練人工智能和機器學習程序。想象一下，90 年代從事數字圖像處理的人工智能工程師，能有多少數字圖像來訓練算法呢？也許是幾千或者幾萬張吧。現在單單數據科學平臺 Kaggle（谷歌的子公司）就擁有超過 1 萬個數據集。互聯網上每天產生的大量數據使訓練算法變得容易得多。第三，高速的互聯網連接使得與大型機構協作變得更加容易。21 世紀的頭 10 年，計算機科學家之間的合作還很困難。如今互聯網的速度已經使谷歌 Colab、Kaggle、Project jupiter 等人工智能項目的協作成為現實。由于這三個因素，我相信這一次人工智能將永遠存在，并會出現許多優秀的應用。

更多矩陣的知識

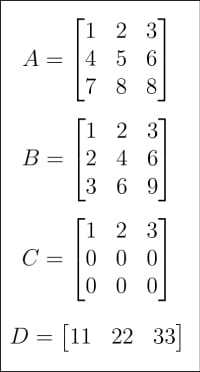圖 1：矩陣 A、B、C、D

在大致了解了人工智能的歷史后，現在是時候回到矩陣與向量這一主題上了。在上一篇文章中，我已經對它們做了簡要介紹。這一次，我們將更深入矩陣的世界。首先看圖 1 和 圖 2，其中顯示了從 A 到 H 共 8 個矩陣。為什么人工智能和機器學習教程中需要這么多矩陣呢？首先，正如前一篇文章中提到的，矩陣是線性代數的核心，而線性代數即使不是機器學習的大腦，也是機器學習的核心。其次，在接下來的討論中，它們每一個都有特定的用途。

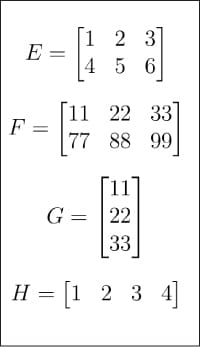圖 2：矩陣 E、F、G、H

讓我們看看矩陣是如何表示的，以及如何獲取它們的詳細信息。圖 3 展示了怎么用 NumPy 表示矩陣 A。雖然矩陣和數組并不完全等價，但實踐中我們經常將它們作為同義詞來使用。

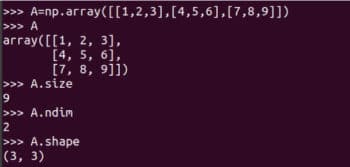圖 3：用 NumPy 表示矩陣 A

我強烈建議你仔細學習如何使用 NumPy 的 array 函數創建矩陣。雖然 NumPy 也提供了 matrix 函數來創建二維數組和矩陣。但是它將在未來被廢棄，所以不再建議使用了。在圖 3 還顯示了矩陣 A 的一些詳細信息。A.size 告訴我們數組中元素的個數。在我們的例子中，它是 9。代碼 A.nidm 表示數組的 維數dimension。很容易看出矩陣 A 是二維的。A.shape 表示矩陣 A 的階數order，矩陣的階數是矩陣的行數和列數。雖然我不會進一步解釋，但使用 NumPy 庫時需要注意矩陣的大小、維度和階數。圖 4 顯示了為什么應該仔細識別矩陣的大小、維數和階數。定義數組時的微小差異可能導致其大小、維數和階數的不同。因此，程序員在定義矩陣時應該格外注意這些細節。

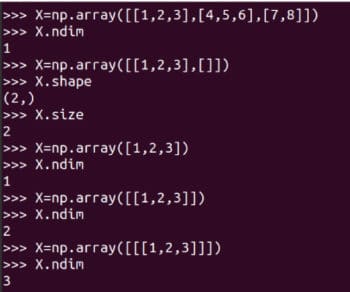圖 4：數組的大小、維數和階數

現在我們來做一些基本的矩陣運算。圖 5 顯示了如何將矩陣 A 和 B 相加。NumPy 提供了兩種方法將矩陣相加，add 函數和 + 運算符。請注意，只有階數相同的矩陣才能相加。例如，兩個 4 × 3 矩陣可以相加，而一個 3 × 4 矩陣和一個 2 × 3 矩陣不能相加。然而，由于編程不同于數學，NumPy 在實際上并不遵循這一規則。圖 5 還展示了將矩陣 A 和 D 相加。記住，這種矩陣加法在數學上是非法的。一種叫做 廣播broadcasting 的機制決定了不同階數的矩陣應該如何相加。我們現在不會討論廣播的細節，但如果你熟悉 C 或 C++，可以暫時將其理解為變量的類型轉換。因此，如果你想確保執行正真數學意義上的矩陣加法，需要保證以下測試為真：

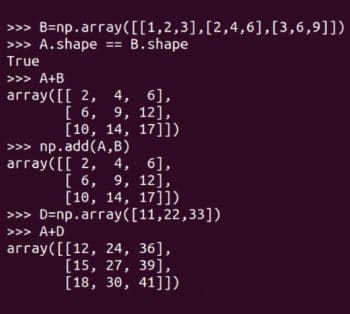圖 5：矩陣相加

A.shape == B.shape

廣播機制也不是萬能的，如果你嘗試把矩陣 D 和 H 相加，會產生一個運算錯誤。

當然除了矩陣加法外還有其它矩陣運算。圖 6 展示了矩陣減法和矩陣乘法。它們同樣有兩種形式，矩陣減法可以由 subtract 函數或減法運算符 - 來實現，矩陣乘法可以由 matmul 函數或矩陣乘法運算符 @ 來實現。圖 6 還展示了 逐元素乘法element-wise multiplication 運算符 * 的使用。請注意，只有 NumPy 的 matmul 函數和 @ 運算符執行的是數學意義上的矩陣乘法。在處理矩陣時要小心使用 * 運算符。

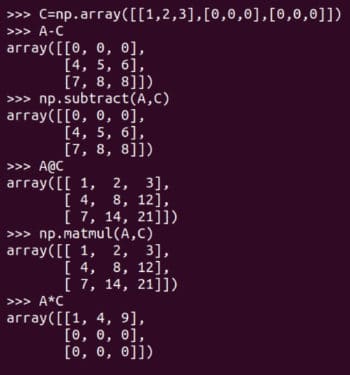圖 6：更多矩陣運算

對于一個 m x n 階和一個 p x q 階的矩陣，當且僅當 n 等于 p 時它們才可以相乘，相乘的結果是一個 m x q 階矩的陣。圖 7 顯示了更多矩陣相乘的示例。注意 E@A 是可行的，而 A@E 會導致錯誤。請仔細閱讀對比 D@G 和 G@D 的示例。使用 shape 屬性，確定這 8 個矩陣中哪些可以相乘。雖然根據嚴格的數學定義，矩陣是二維的，但我們將要處理更高維的數組。作為例子，下面的代碼創建一個名為 T 的三維數組。

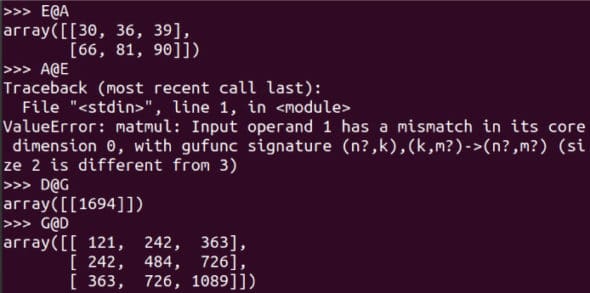圖 7：更多矩陣乘法的例子

T = np.array([[[11,22], [33,44]], [[55,66], [77,88]]])

Pandas

到目前為止，我們都是通過鍵盤輸入矩陣的。如果我們需要從文件或數據集中讀取大型矩陣并處理，那該怎么辦呢？這時我們就要用到另一個強大的 Python 庫了——Pandas。我們以讀取一個小的 CSV （逗號分隔值comma-separated value）文件為例。圖 8 展示了如何讀取 cricket.csv 文件，并將其中的前三行打印到終端上。在本系列的后續文章中將會介紹 Pandas 的更多特性。

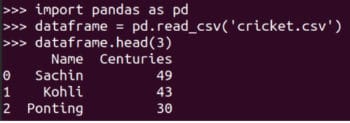圖 8：用 Pandas 讀取 CSV 文件

矩陣的秩

矩陣的 秩Rank 是由它的行（列）張成的向量空間的維數。如果你還記得大學線性代數的內容的話，你一定對維數、向量空間和張成還有印象，那么你也應該能理解矩陣的秩的含義了。但如果你不熟悉這些術語，那么可以簡單地將矩陣的秩理解為矩陣中包含的信息量。當然，這又是一種未來方便理解而過度簡化的說法。圖 9 顯示了如何用 NumPy 求矩陣的秩。矩陣 A 的秩為 3，因為它的任何一行都不能從其它行中得到。矩陣 B 的秩為 1，因為第二行和第三行可以由第一行分別乘以 2 和 3 得到。矩陣 C 只有一個非零行，因此秩為 1。同樣的，其它矩陣的秩也不難理解。矩陣的秩與我們的主題關系密切，我們會在后續文章中再提到它。

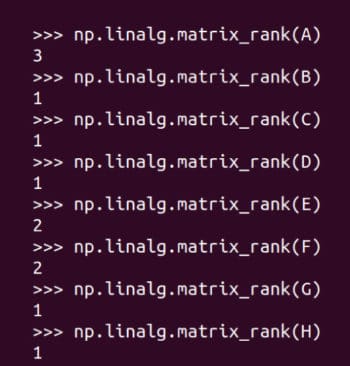圖 9：求矩陣的秩

本次的內容就到此結束了。在下一篇文章中，我們將擴充工具庫，以便它們可用于開發人工智能和機器學習程序。我們還將更詳細地討論 神經網絡neural network、監督學習supervised learning、無監督學習unsupervised learning 等術語。此外，從下一篇文章開始，我們將使用 JupyterLab 代替 Linux 終端。