矩陣模擬!Transformer大模型3D可視化,GPT-3、Nano-GPT每一層清晰可見
模擬人類神經元,不斷進化的Transformer模型,一直以來都深不可測。
許多科學家都試著打開這個黑盒,看看究竟是如何工作的。
而現在,大模型的矩陣世界,真的被打開了!
一位軟件工程師Brendan Bycroft制作了一個「大模型工作原理3D可視化」網站霸榜HN,效果非常震撼,讓你秒懂LLM工作原理。
 圖片
圖片
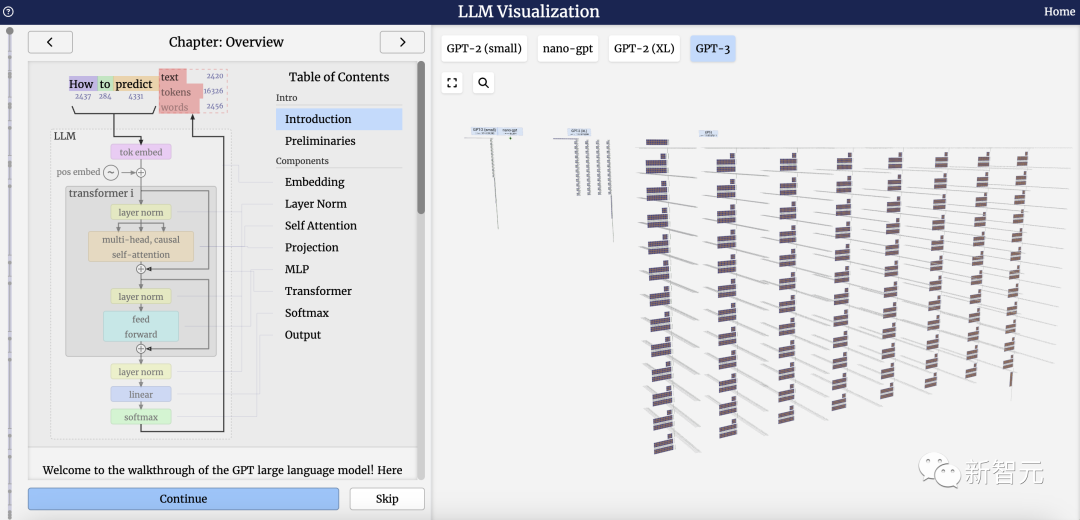
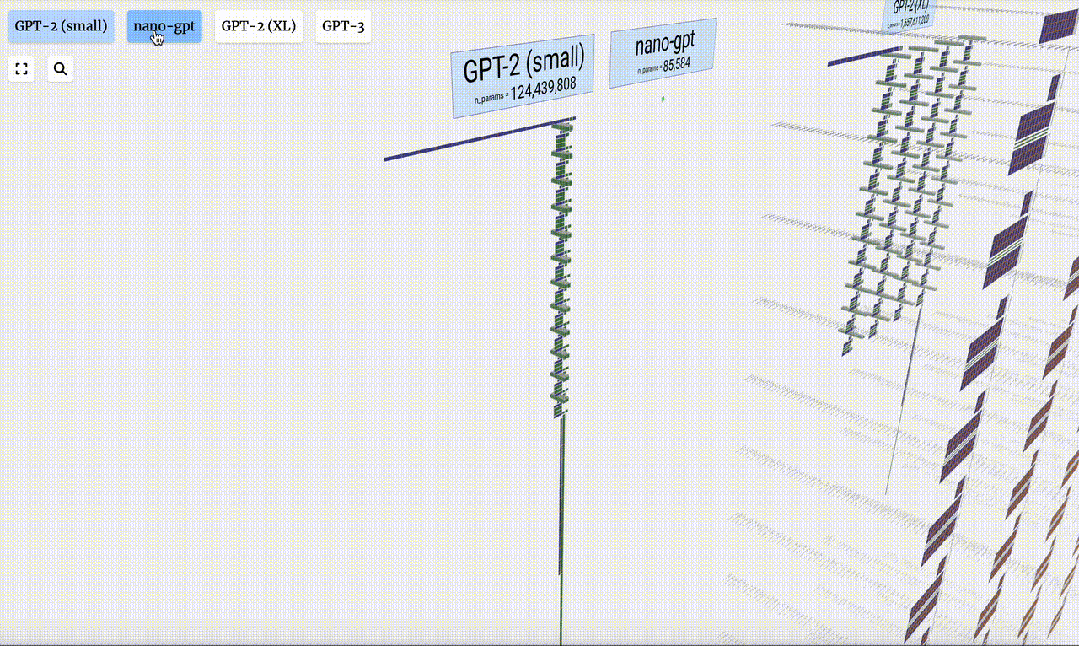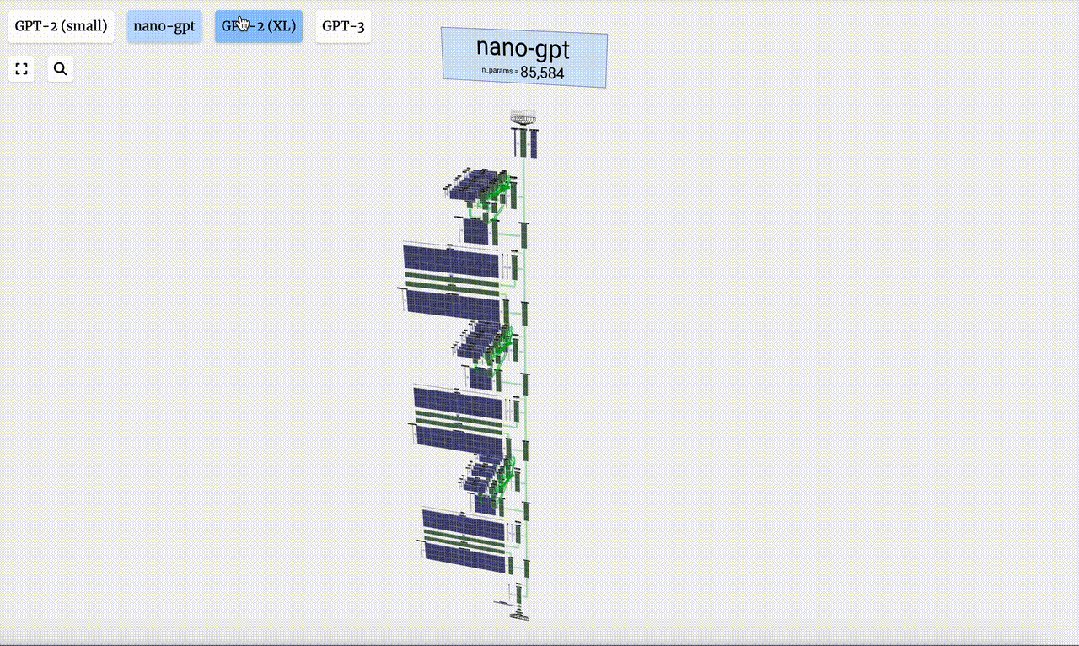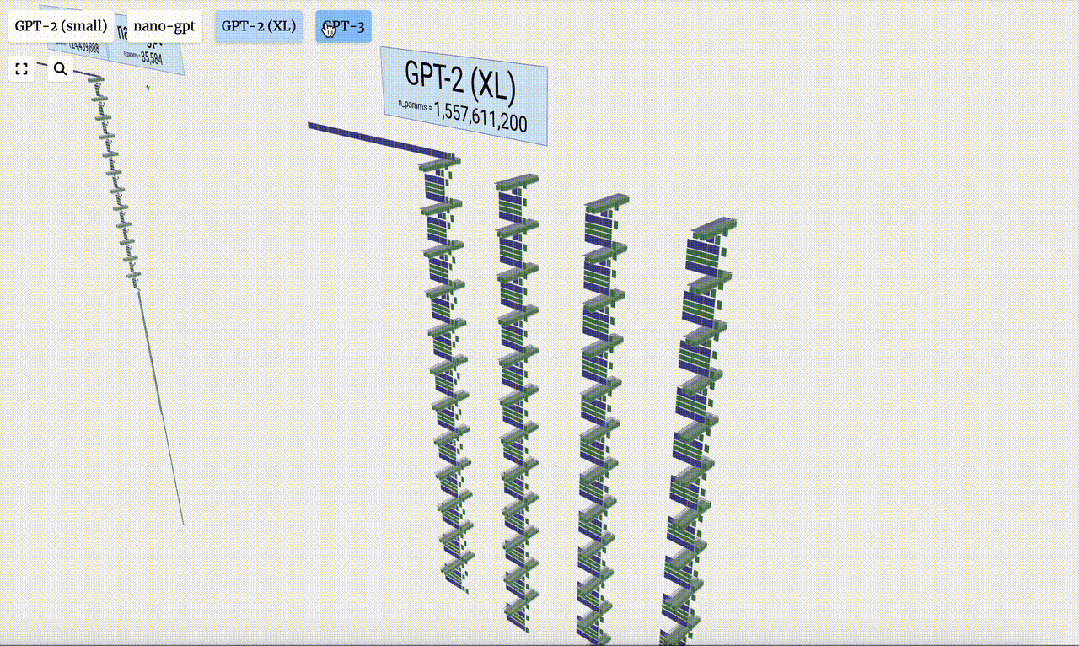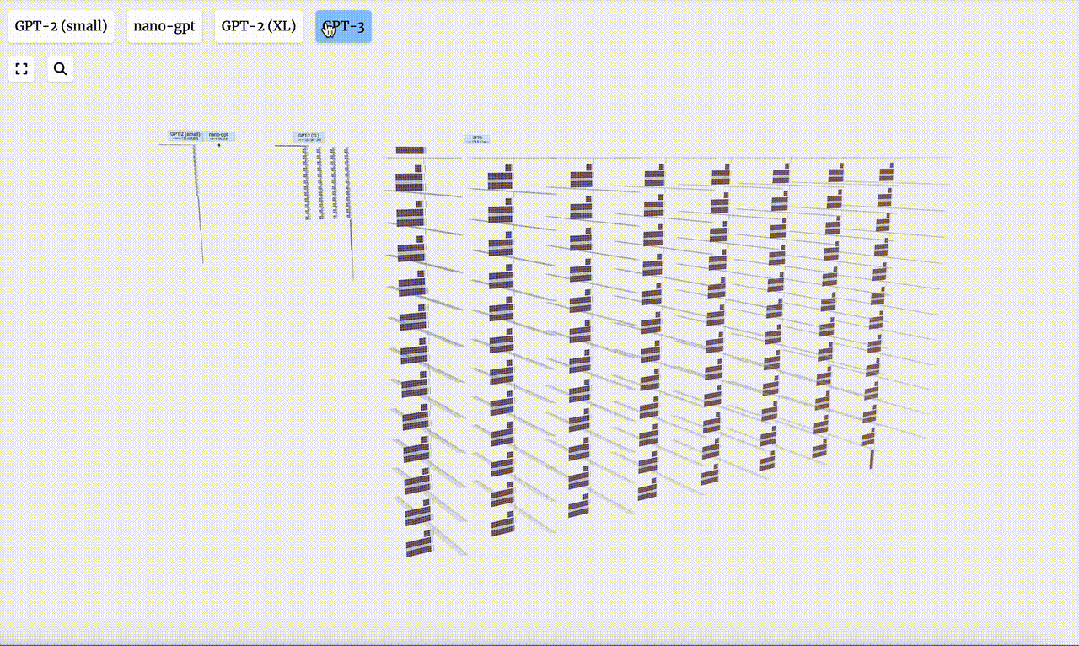
1750億參數的GPT-3,模型層足足有8列,密密麻麻沒遍布了整個屏幕。
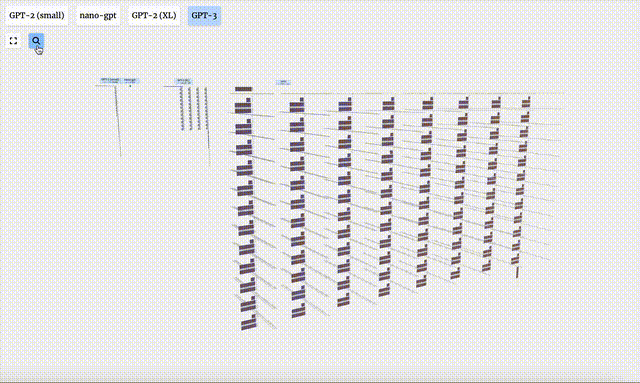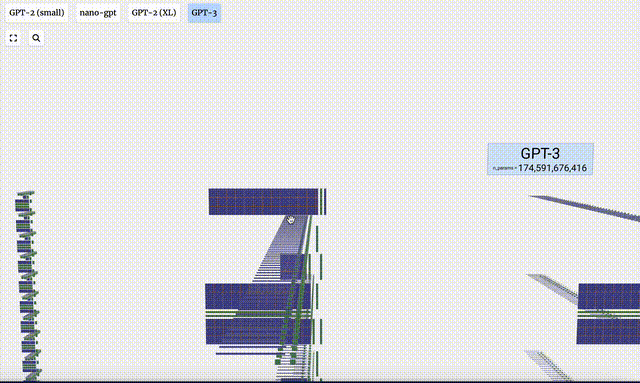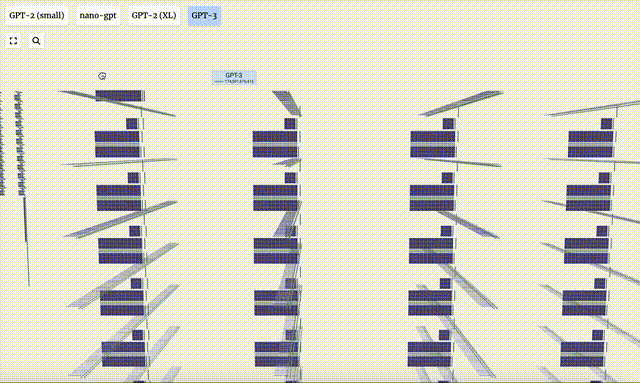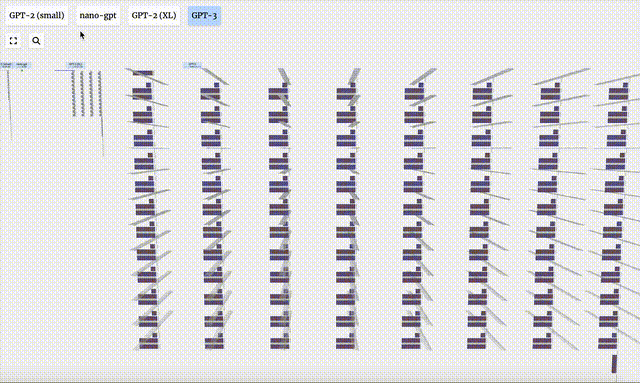 圖片
圖片
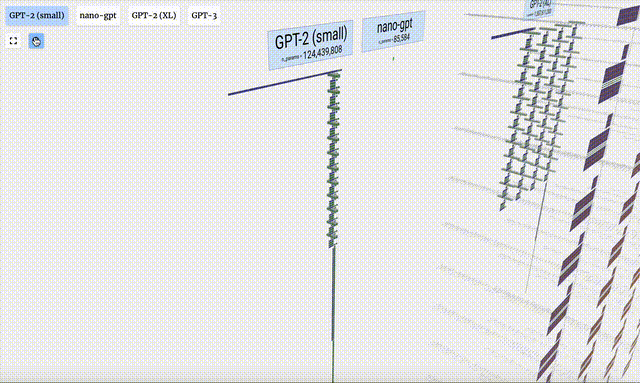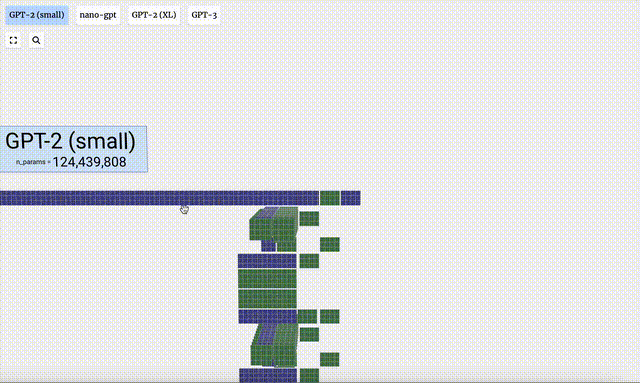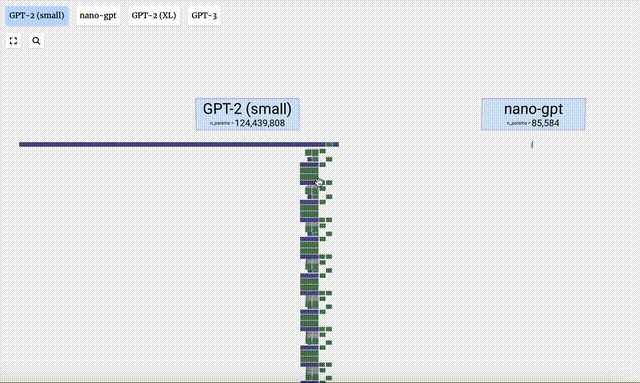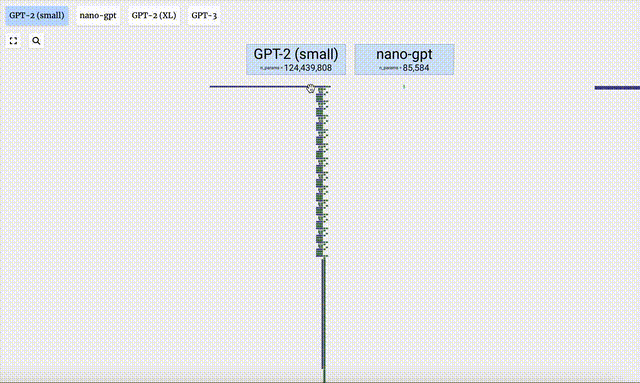
GPT-2模型不同參數版本的架構可視化,差異巨大。如下是有150億參數GPT-2(XL),以及有1.24億參數GPT-2(Small)。
 圖片
圖片
 圖片
圖片
這個3D模型可視化還展示了,大模型生成內容的每一步。
這里,Bycroft主要分解了OpenAI科學家Andrej Karpathy打造的輕量級的GPT模型——NanoGPT,參數量為85000。
 圖片
圖片
地址:https://bbycroft.net/llm
看過這個可視化圖,你就可以了解ChatGPT的大腦。

從GPT-2(Small)到GPT-3的參數規模的跨越,讓人嘆為觀止。
 圖片
圖片
Bycroft稱,這個指南側重于模型的推理,而非訓練,只是機器學習中的一小部分。在具體例子中,模型的權重已經預訓練完成,使用推理過程來生成輸出。
當然了,這個可視化網站也是收到了Karpathy在PyTorch中創建的minGPT,以及YouTube視頻系列「Neural Networks: Zero to Hero」的啟發。
接下來,一起深入來了解,Transformer模型每一層。
介紹
為了方便進行演示,Brendan Bycroft給NanoGPT布置了一個非常簡單的任務:
獲取一個由六個字母組成的序列:C B A B B C,并按字母順序排序,即「ABBBCC」。
 圖片
圖片
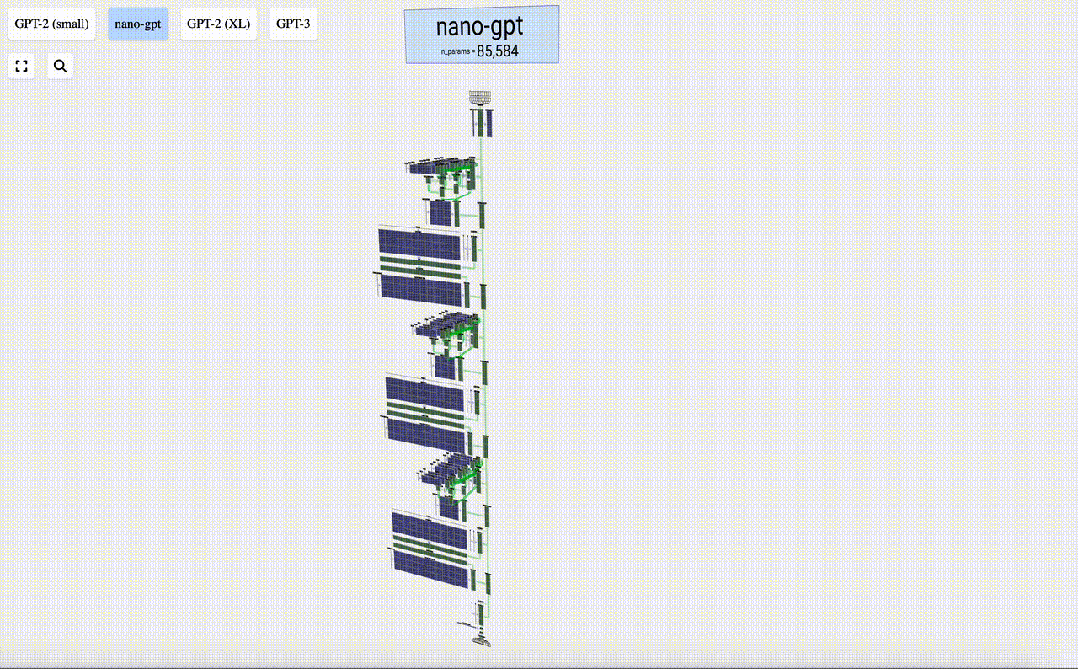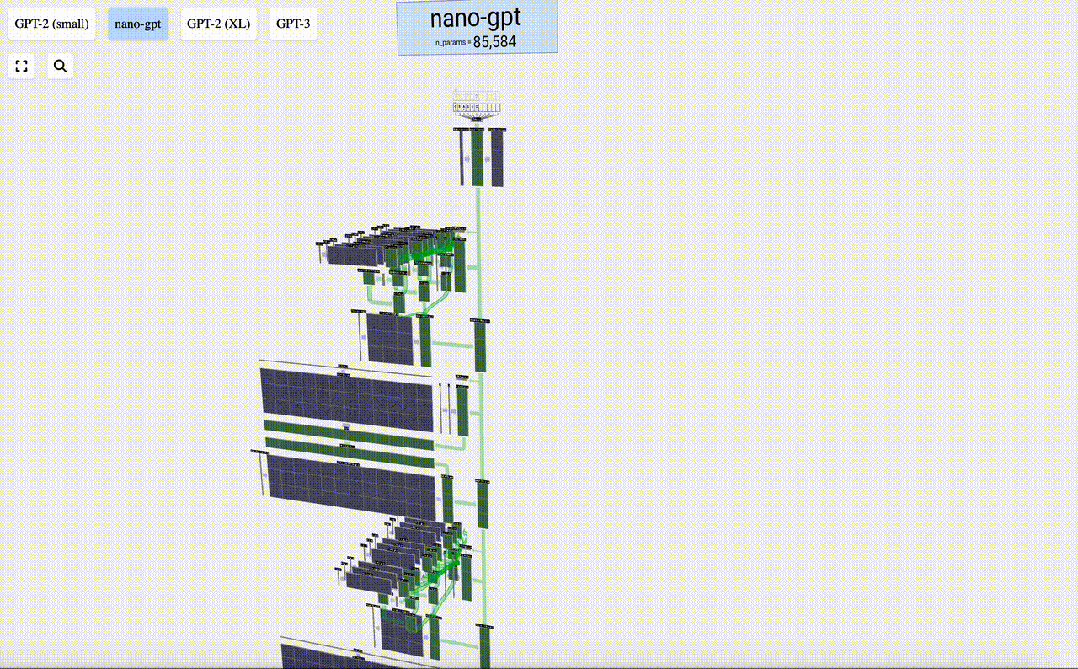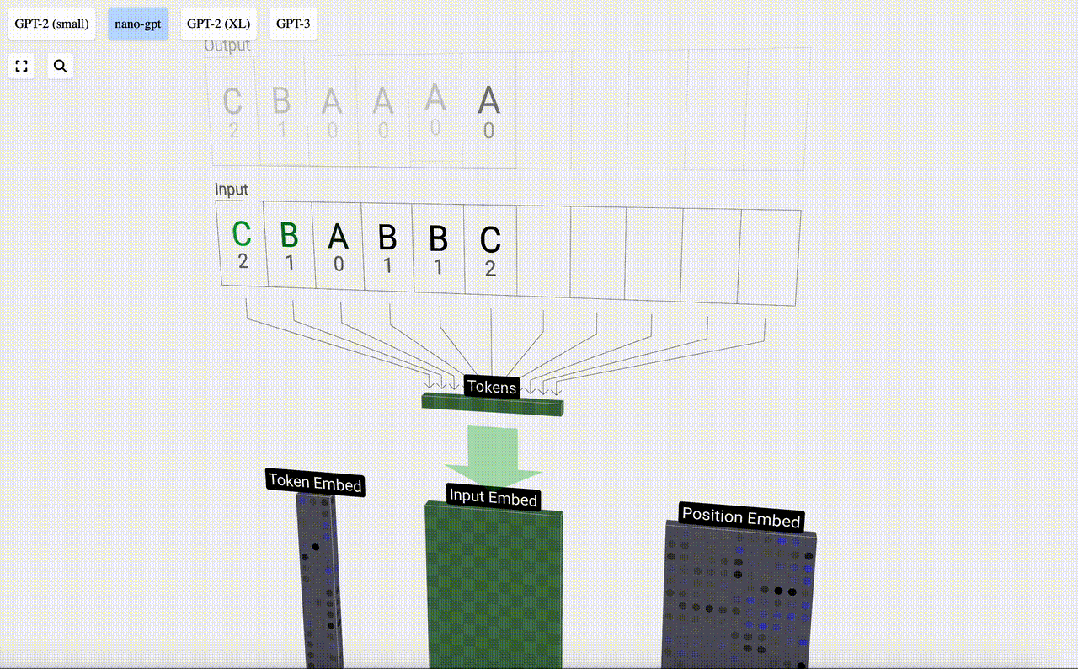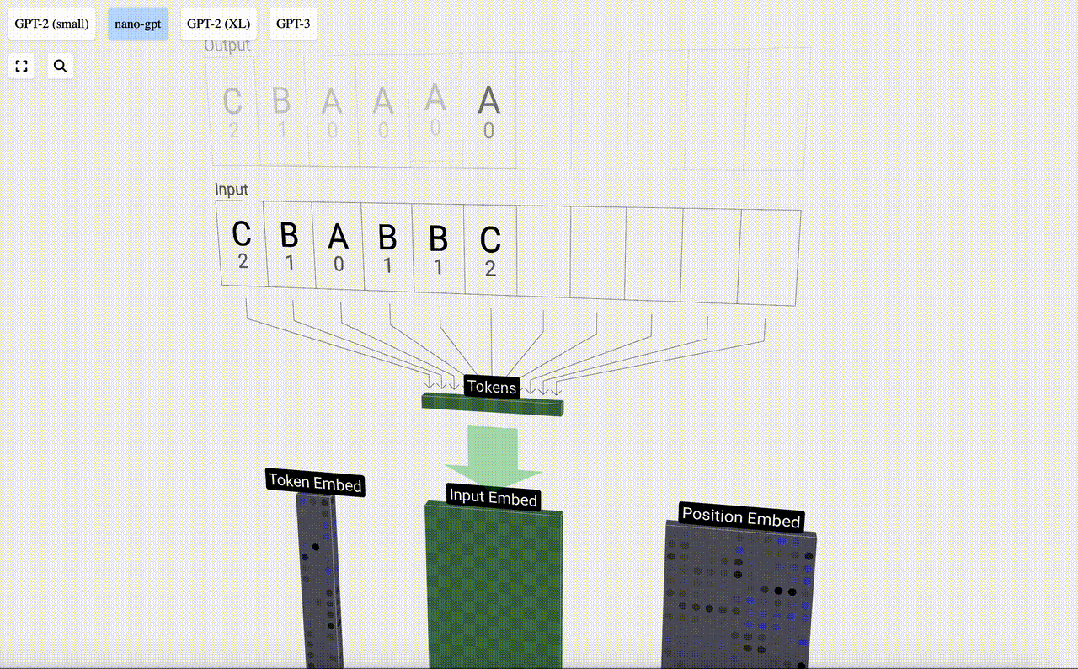
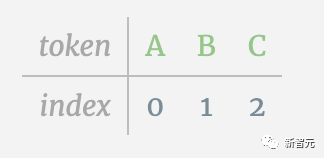
我們將每一個字母稱為token,模型的不同token集合構成了它的詞匯表:
 圖片
圖片
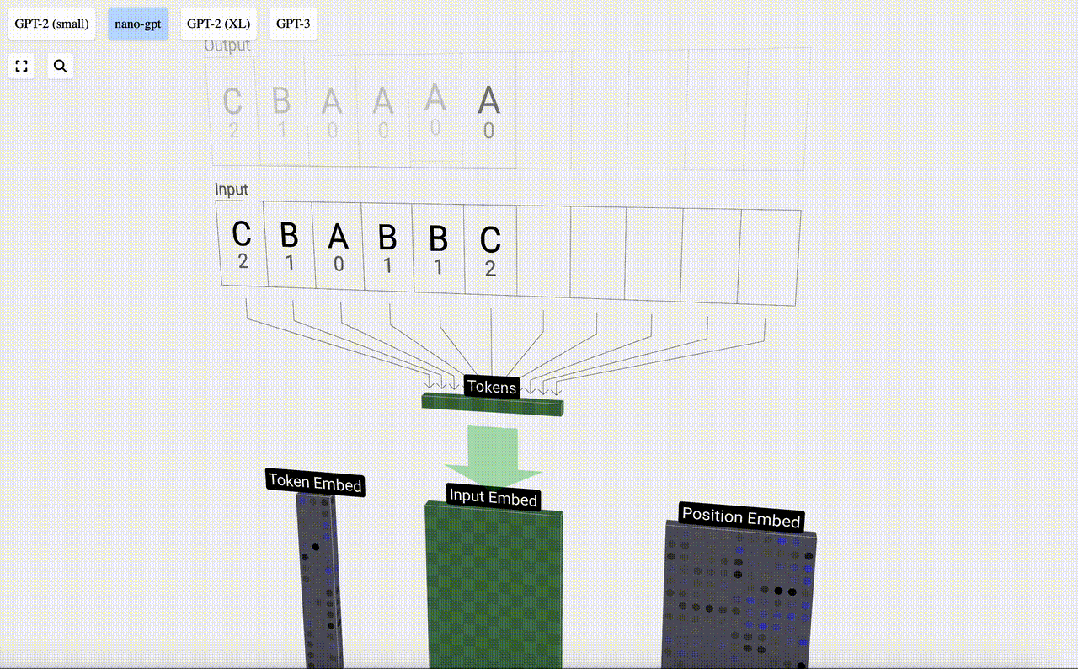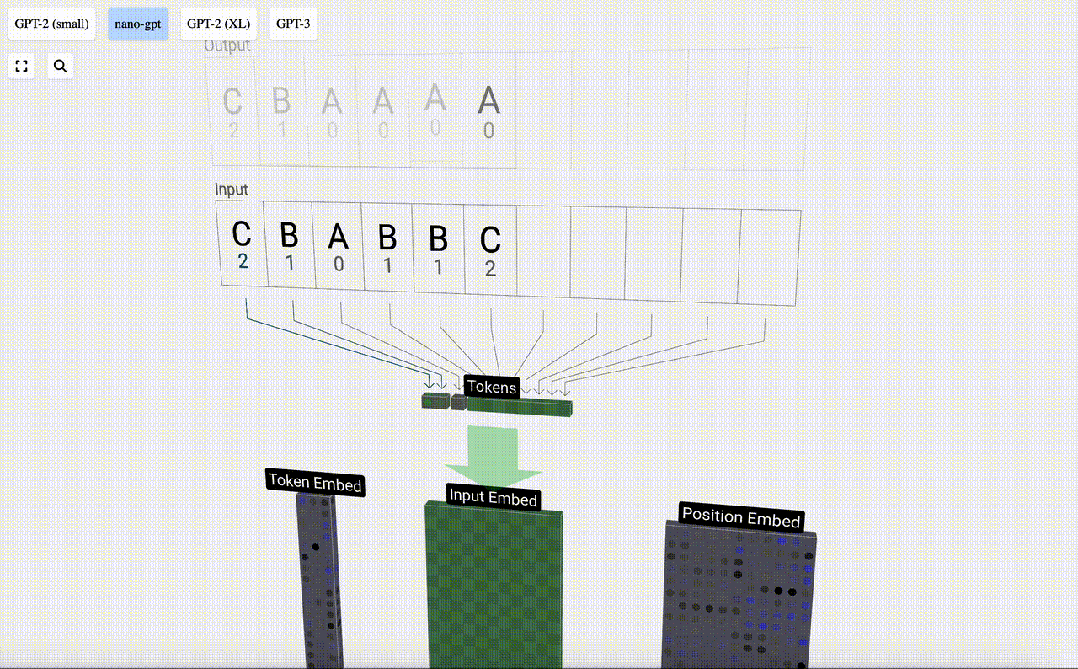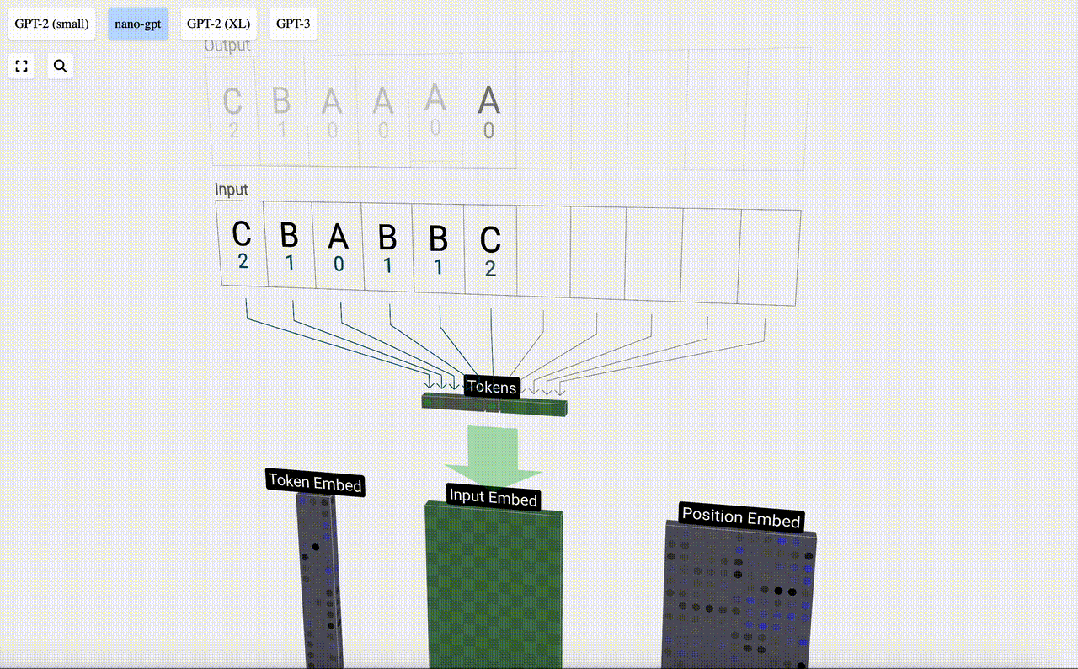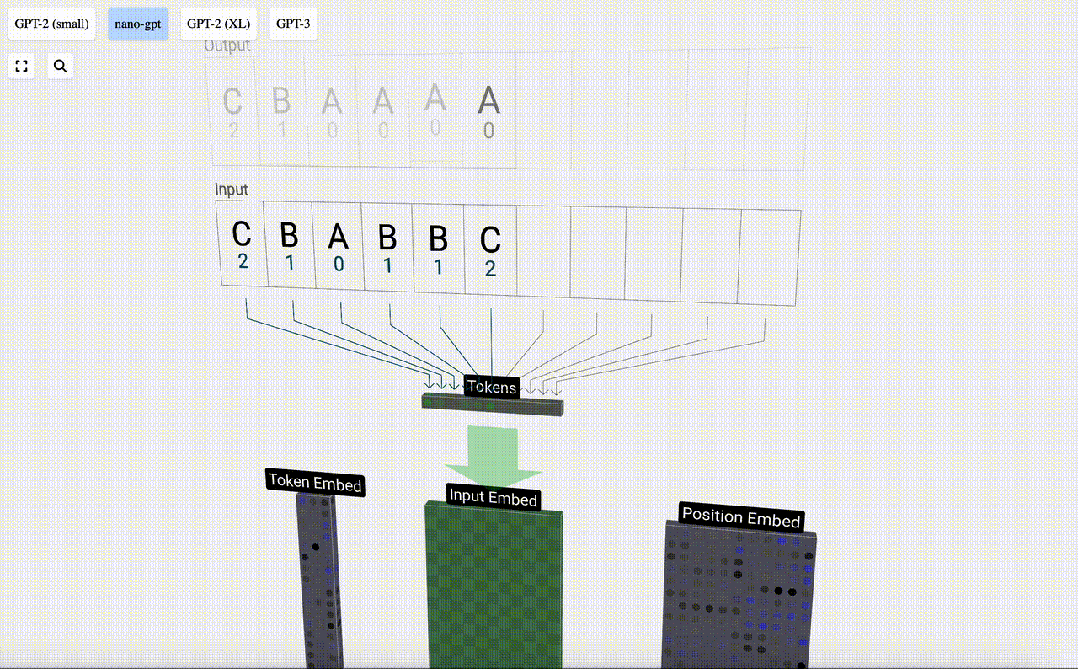
這個表中,每個token都被分配了一個數字,它是token index。現在我們可以將這一系列數字輸入到模型中:「2 1 0 1 1 2」
 圖片
圖片
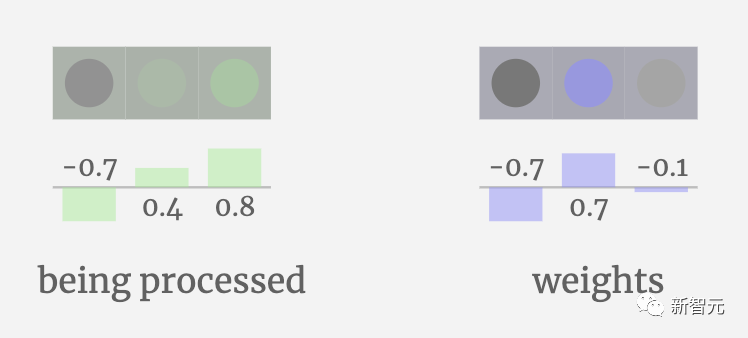
在3D視圖中,每個綠色單元格表示一個正在處理的數字,每個藍色單元格表示權重。
 圖片
圖片
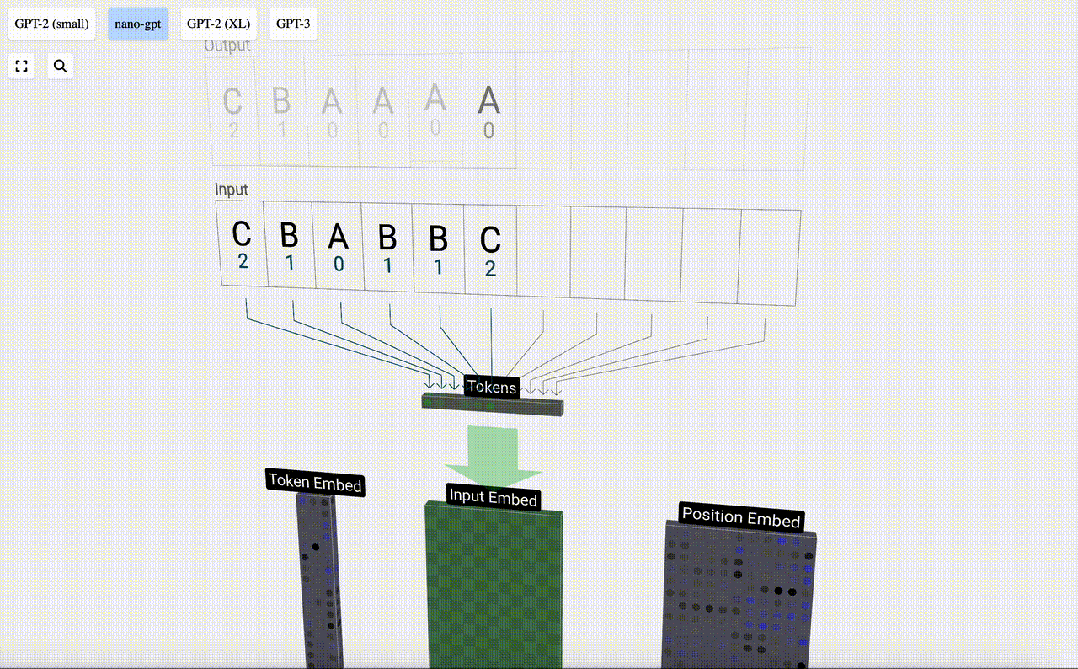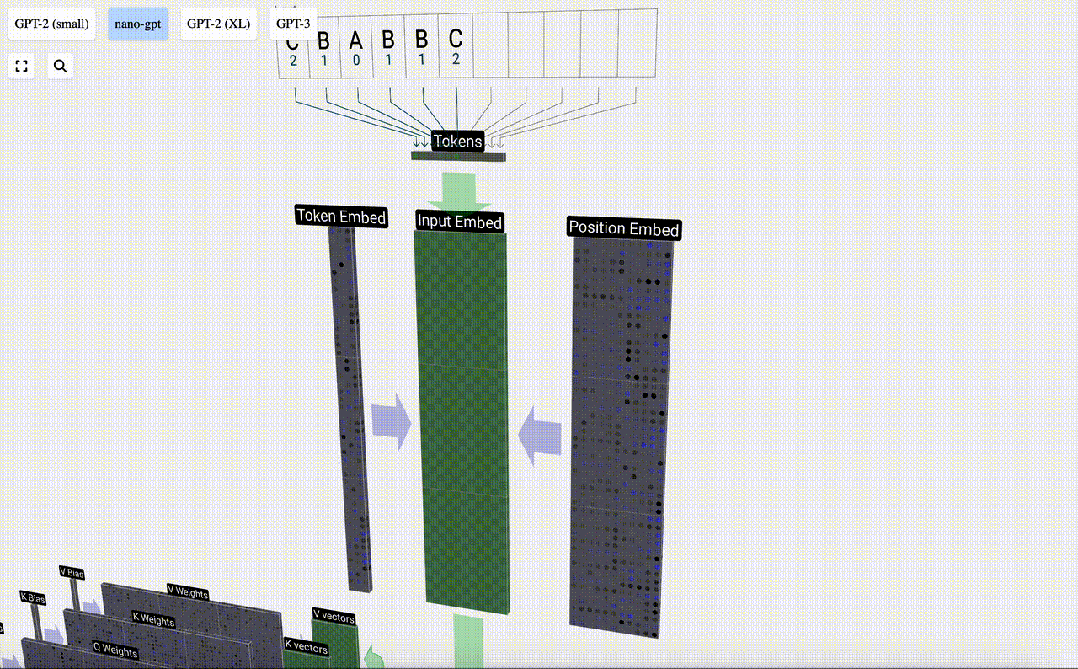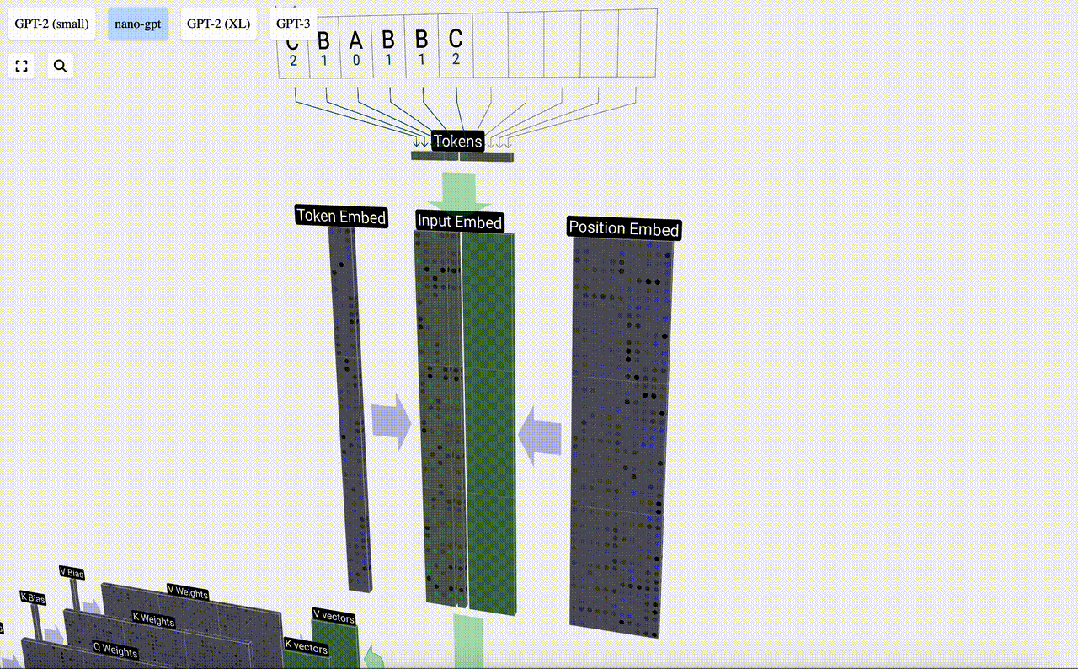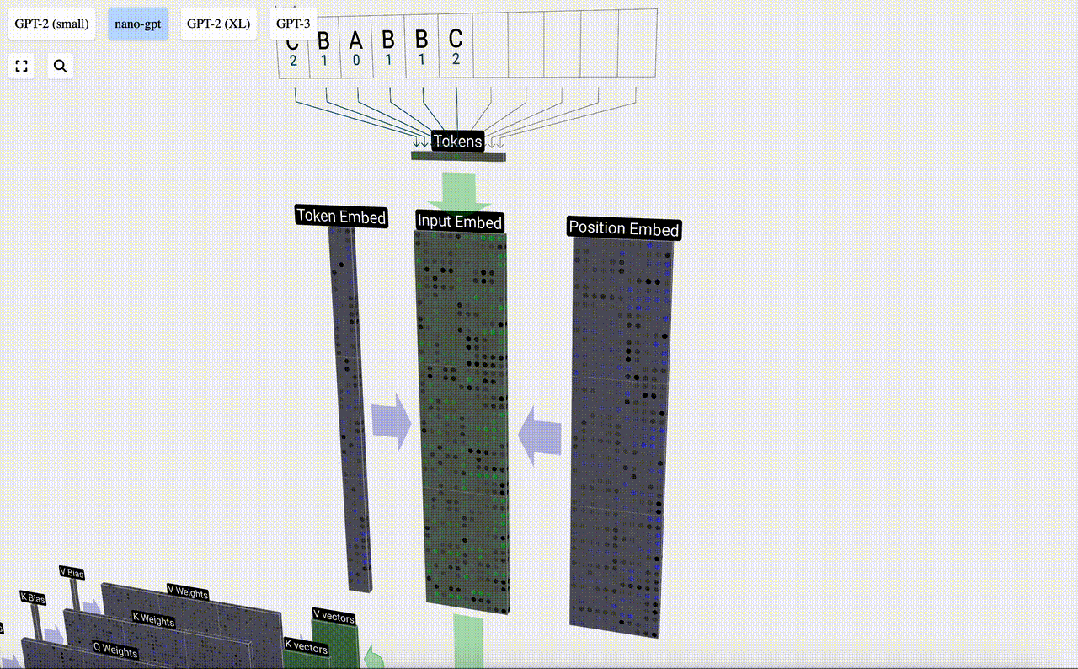
序列中的每個數字首先被轉換為一個48元素向量,這就是所謂的「嵌入」(embedding)。
 圖片
圖片
然后,「嵌入」被輸入模型,傳遞通過一系列Transformer層,最后到達底層。
 圖片
圖片
那么輸出是什么呢?
對序列中下一個token的預測。因此,在序列中第6個token處,得到了下一個token將是「A」、「B」或「C」的概率。
在這種情況下,模型非常確定會是「A」。
現在,我們可以將這一預測反饋到模型的頂層,并重復整個過程。
嵌入
我們之前看到過,如何使用一個簡單的查找表(lookup table)將token映射為一串整數。
這些整數,即標記token index,是我們在模型中第一次,也是唯一一次看到的整數。從這里開始,我們將使用浮點數(十進制數)進行運算。
以第4個token(index 3)為例,看看是如何被用來生成輸入嵌入的第4列向量的。
 圖片
圖片
我們使用token index(在本例中為B = 1)來選擇左側token嵌入矩陣的第二列。請注意,我們在這里使用的是從0開始的index,因此第一列位于index 0處。
這將產生一個大小為C=48的列向量,我們將其描述為「token嵌入」(token embedding)。
 圖片
圖片
由于我們主要查看的是位于第4個位置的 (t = 3) token B,因此我們將采用「位置嵌入矩陣」的第4列。
這也會產生一個大小為C=48的列向量,我們將其描述為位置嵌入(position embedding)。
 圖片
圖片
請注意,這兩個位置和token嵌入都是在訓練期間學習的(由藍色表示)。
現在我們有了這兩個列向量,我們只需將它們相加即可生成另一個大小為C=48的列向量。
 圖片
圖片
現在,我們對輸入序列中的所有token運行相同的過程,創建一組包含token值及其位置的向量。
 圖片
圖片
(隨意停在輸入嵌入矩陣上的單個單元格上,可以查看計算及其來源。)
我們看到,對輸入序列中的所有token運行此過程,會產生一個大小為TxC的矩陣。
T代表時間,也就是說,你可以將序列中稍后的token看作是時間上稍后的token。C代表通道(channel),但也稱為「特征」或「維度」或「嵌入大小」。
這個矩陣,我們稱之為「輸入嵌入」(input embedding),并通過模型向下傳遞。
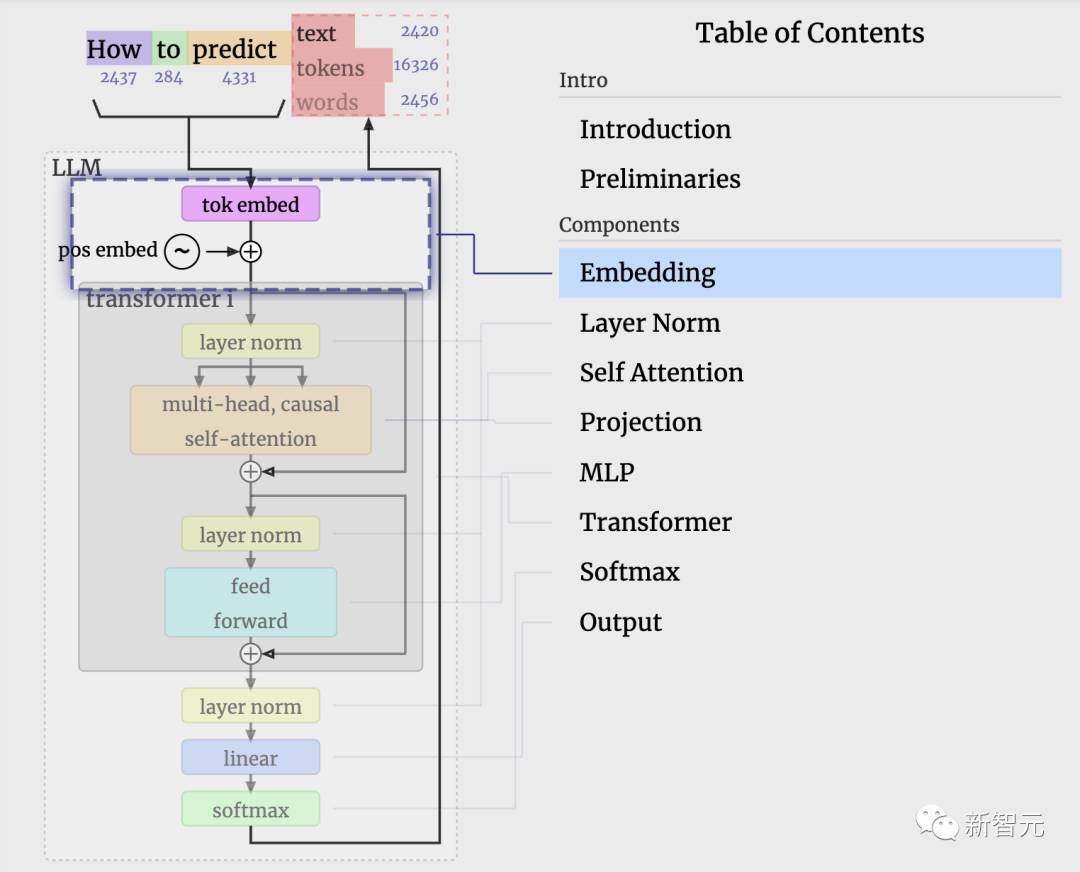
在本指南中,我們將看到由T列(每列長度為 C)組成的矩陣集合。
 圖片
圖片
Layer Norm
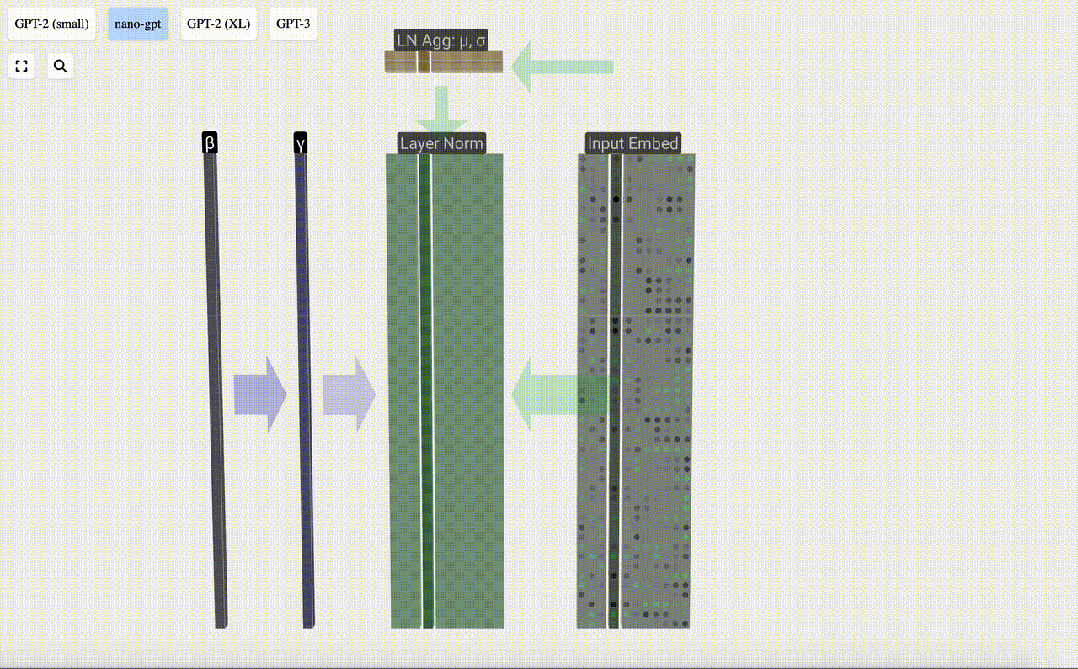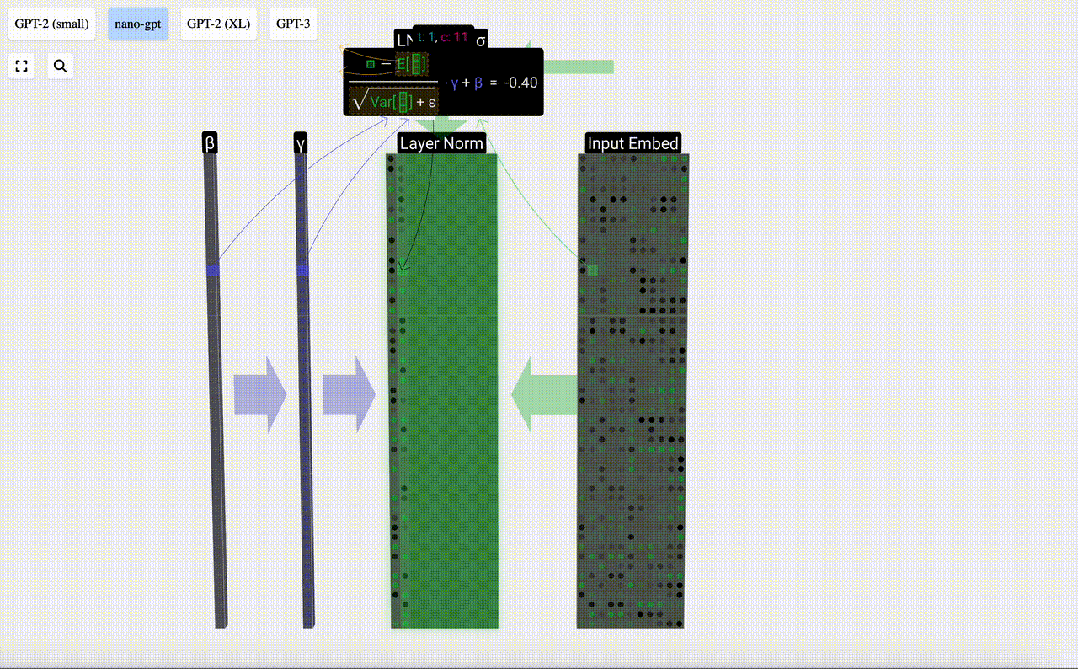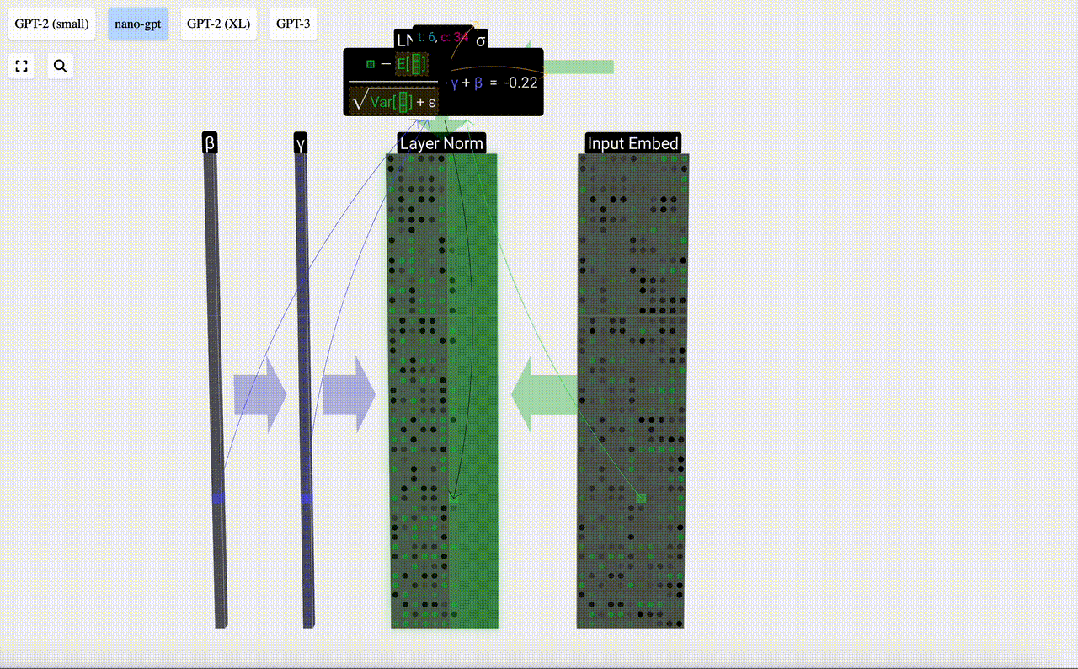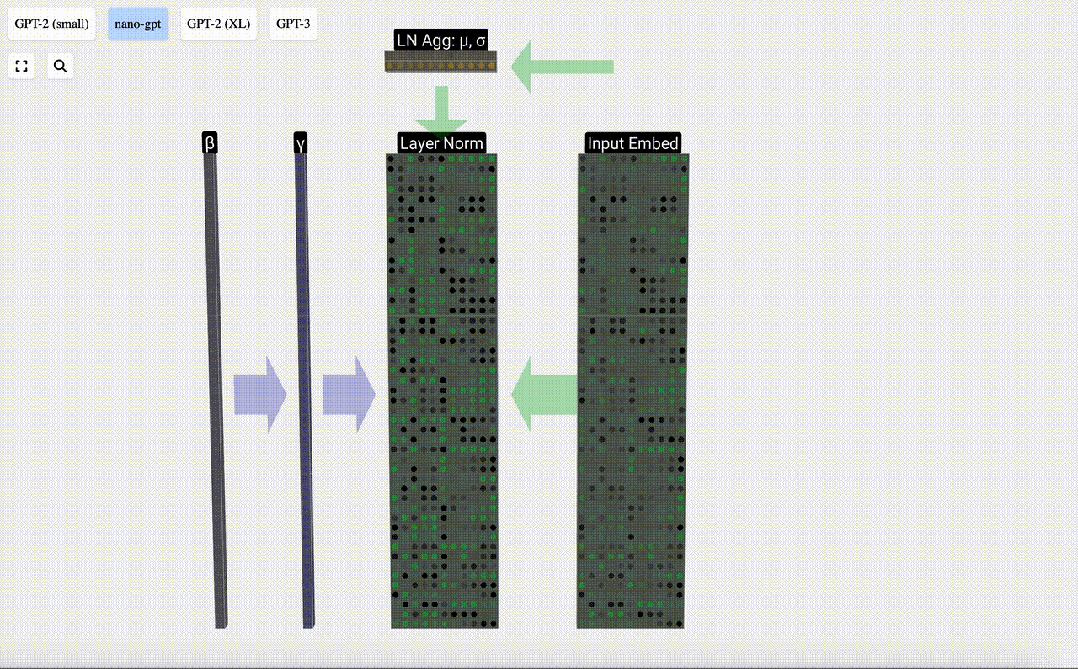
上一節的「輸入嵌入」矩陣是第一個Transformer模塊的輸入。
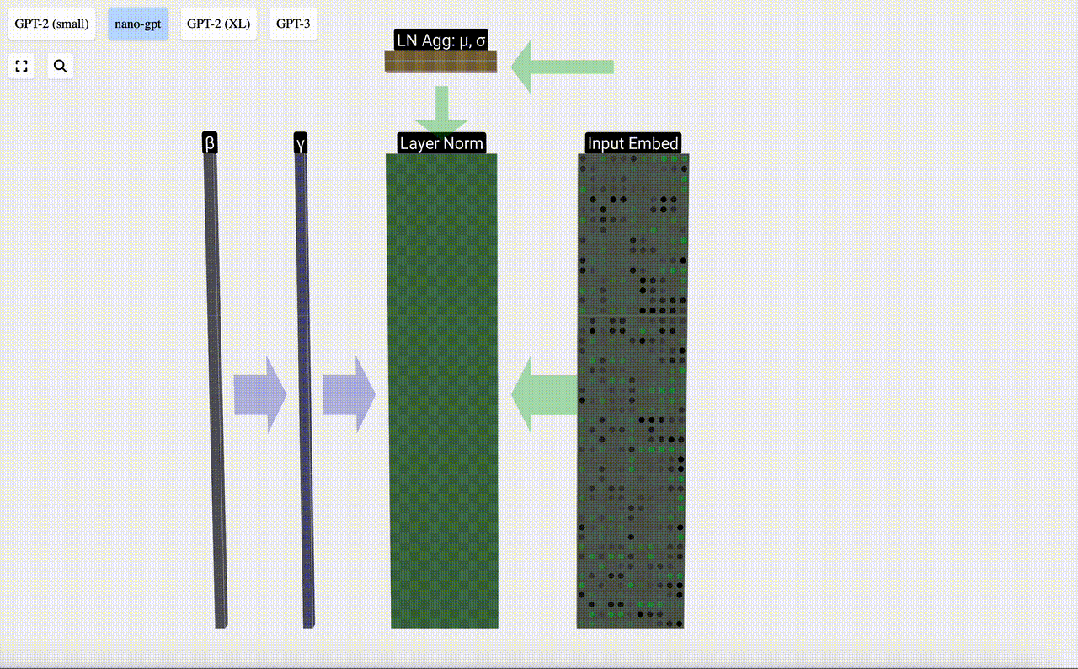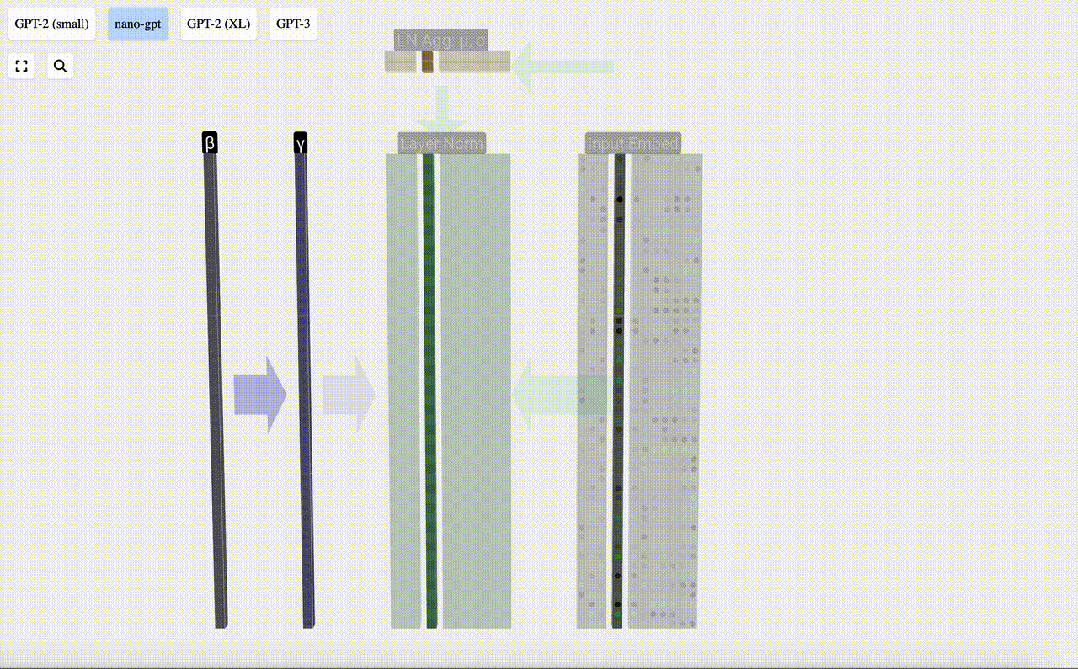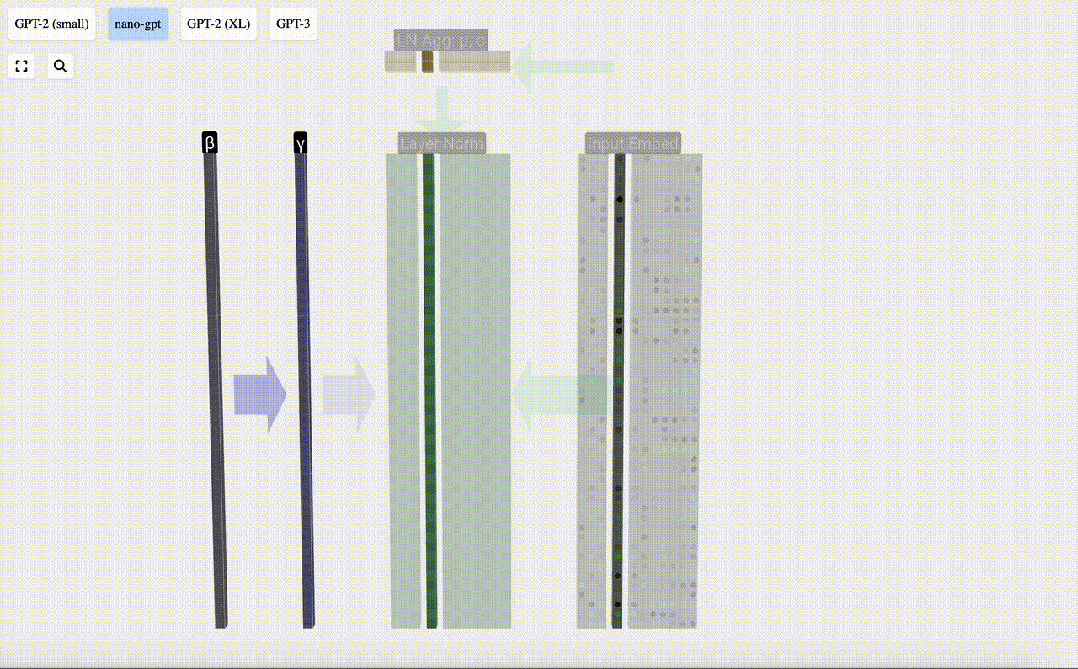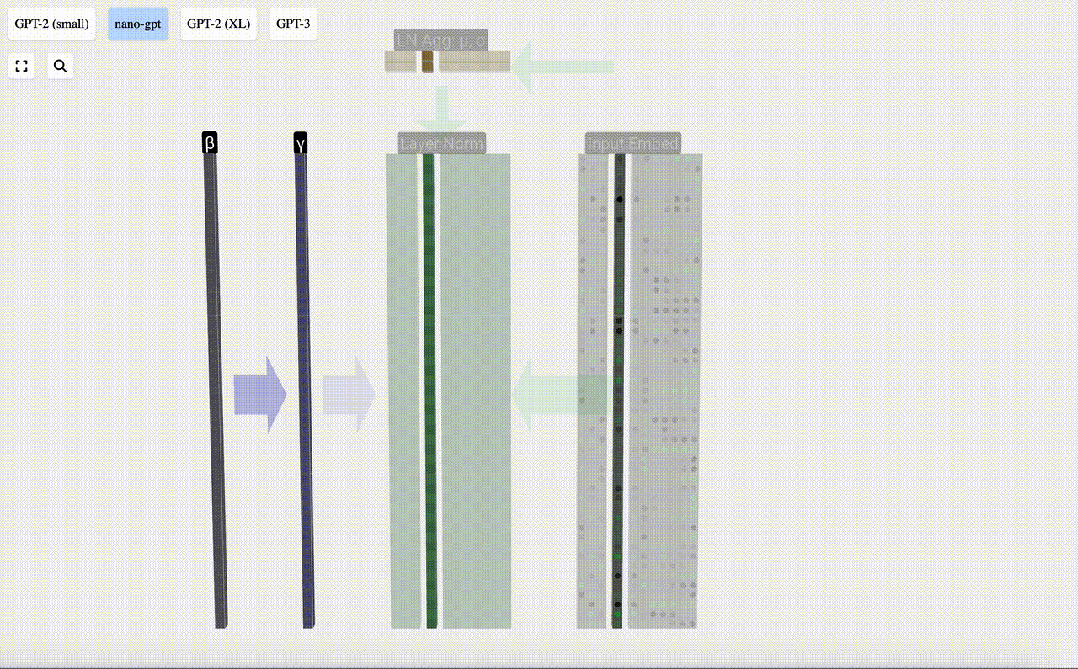
Transformer模塊的第一步是對該矩陣進行「層歸一化」(Layer Norm)處理。這是對矩陣每列的值分別進行歸一化的操作。
 圖片
圖片
歸一化是深度神經網絡訓練中的一個重要步驟,它有助于提高模型在訓練過程中的穩定性。
我們可以分別看待每一列,所以現在先關注第4列(t=3)。
 圖片
圖片
我們的目標是使該列的平均值等于0,標準偏差等于1。為此,我們要找出該列的這兩個量(平均值 (μ) 和標準偏差 (σ)),然后減去平均值,再除以標準偏差。
 圖片
圖片
這里我們使用E[x]表示平均值,Var[x]表示方差(長度為C的列)。方差就是標準差的平方。ε項
是為了防止除以零。
我們在聚合層中計算并存儲這些值,因為我們要將它們應用于列中的所有值。
最后,在得到歸一化值后,我們將列中的每個元素乘以學習權重 (γ),然后加上偏置 (β),最終得到歸一化值。
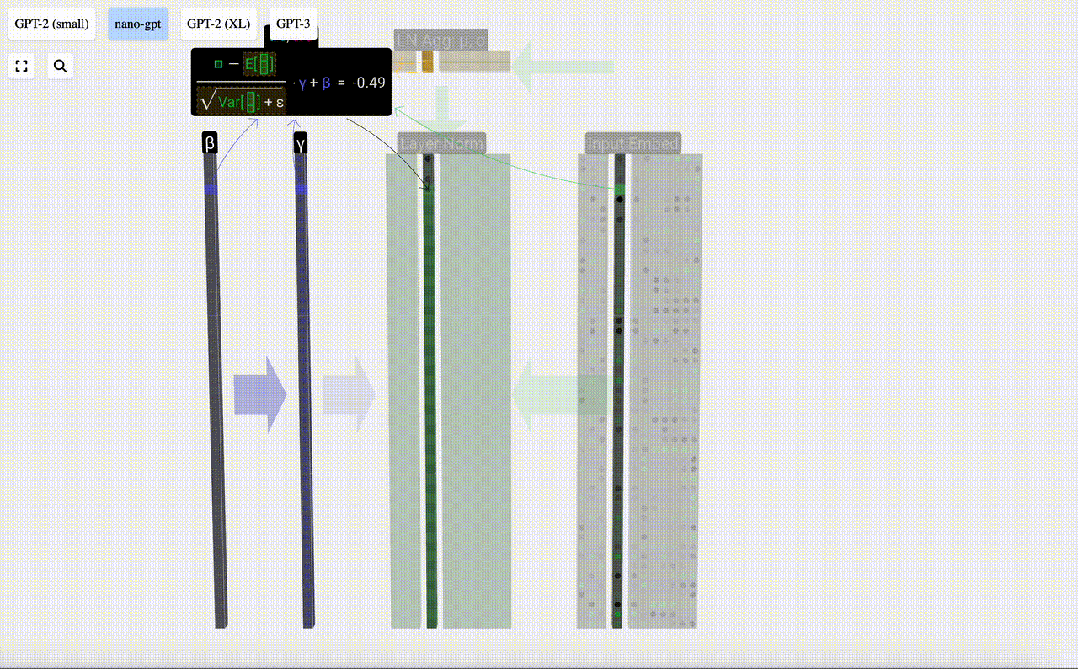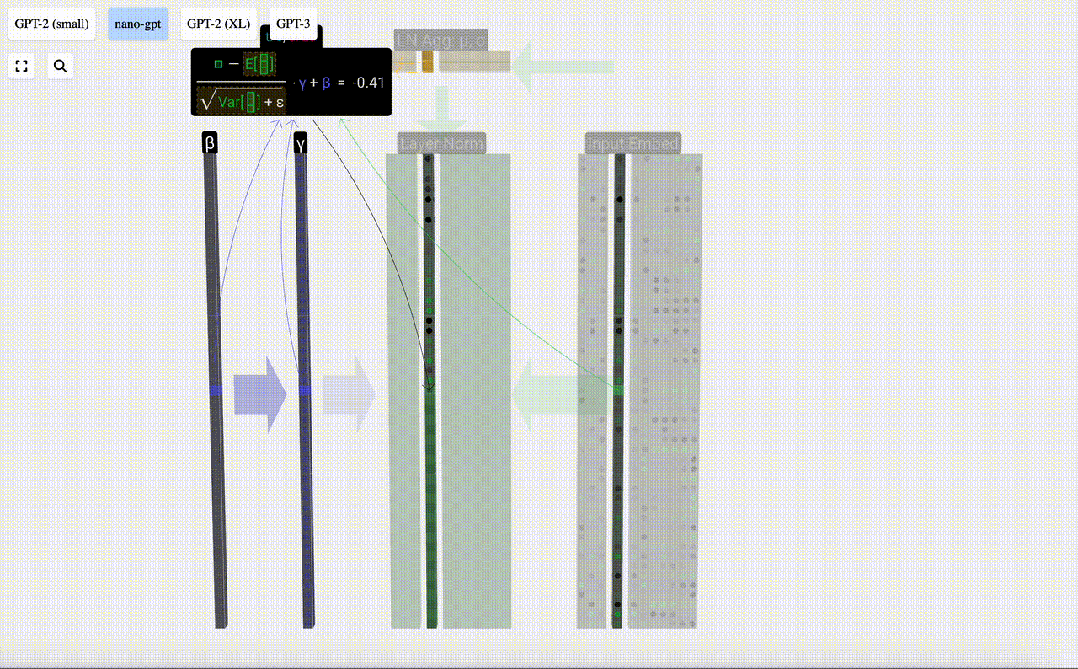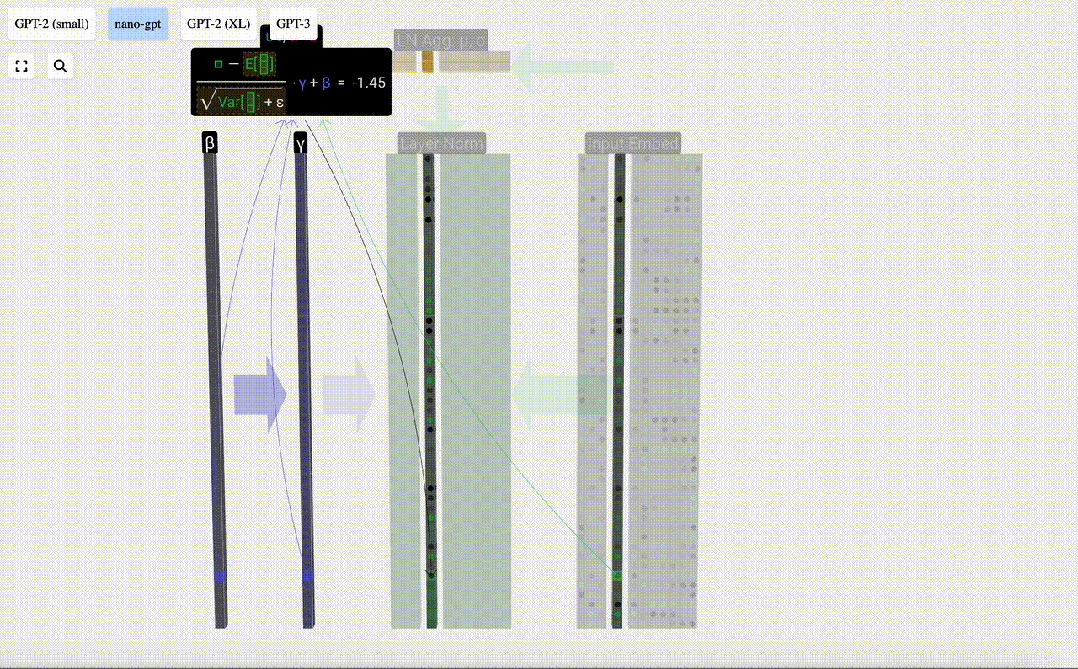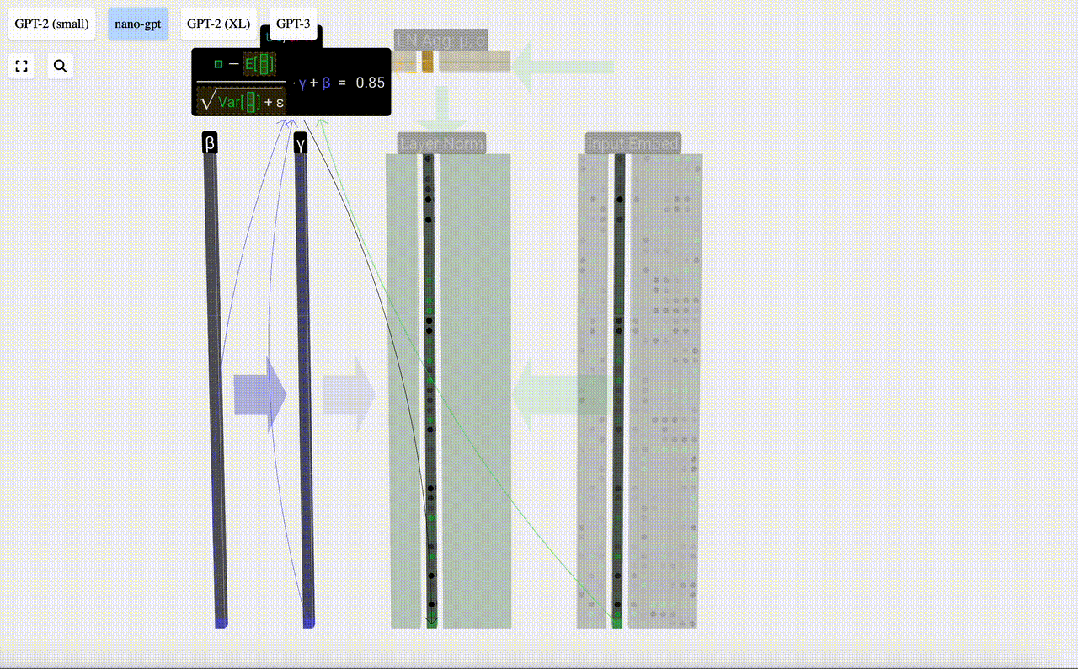 圖片
圖片
我們在「輸入嵌入」矩陣的每一列上執行這一歸一化操作,得到的結果就是歸一化后的「輸入嵌入」,并將其傳遞給自注意力層。
 圖片
圖片
自注意力
自注意力層或許是Transformer和GPT的核心。在這一階段,「輸入嵌入」矩陣中的各列相互「對話」。到目前為止,在所有其他階段,各列都是獨立存在的。
自注意力層由幾個頭組成,我們現在只關注其中一個。
 圖片
圖片
第一步是從歸一化輸入嵌入矩陣的C列中為每一列生成三個向量。這些向量分別是Q、K和V向量:
Q:查詢向量
K:鍵向量
V:值向量
要生成這些向量中的一個,我們要執行矩陣-向量乘法,并加上偏置。
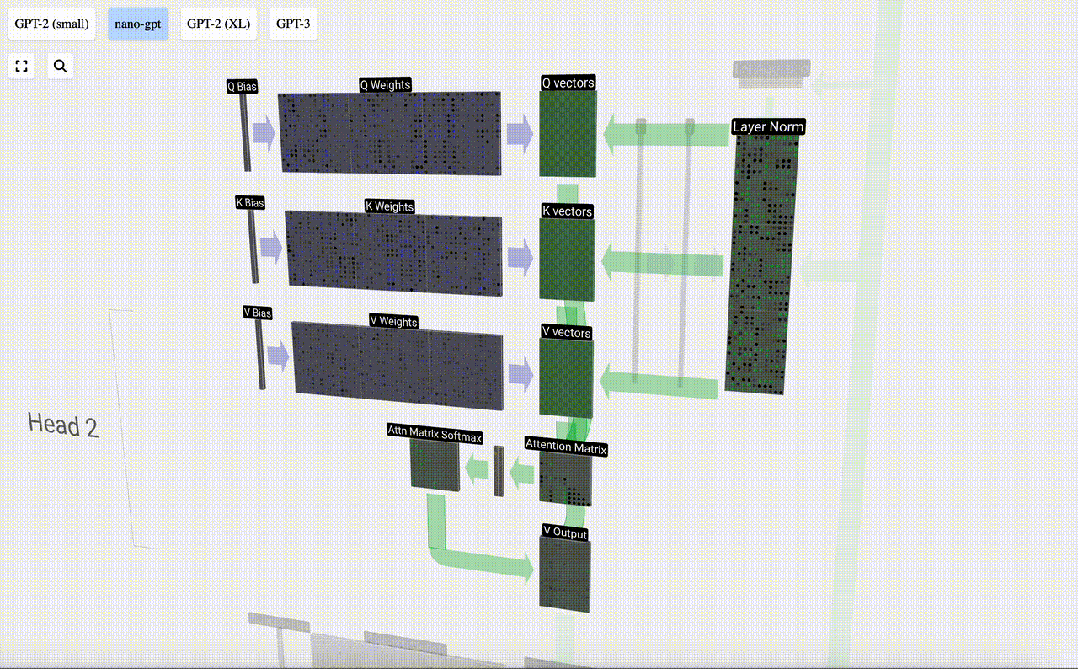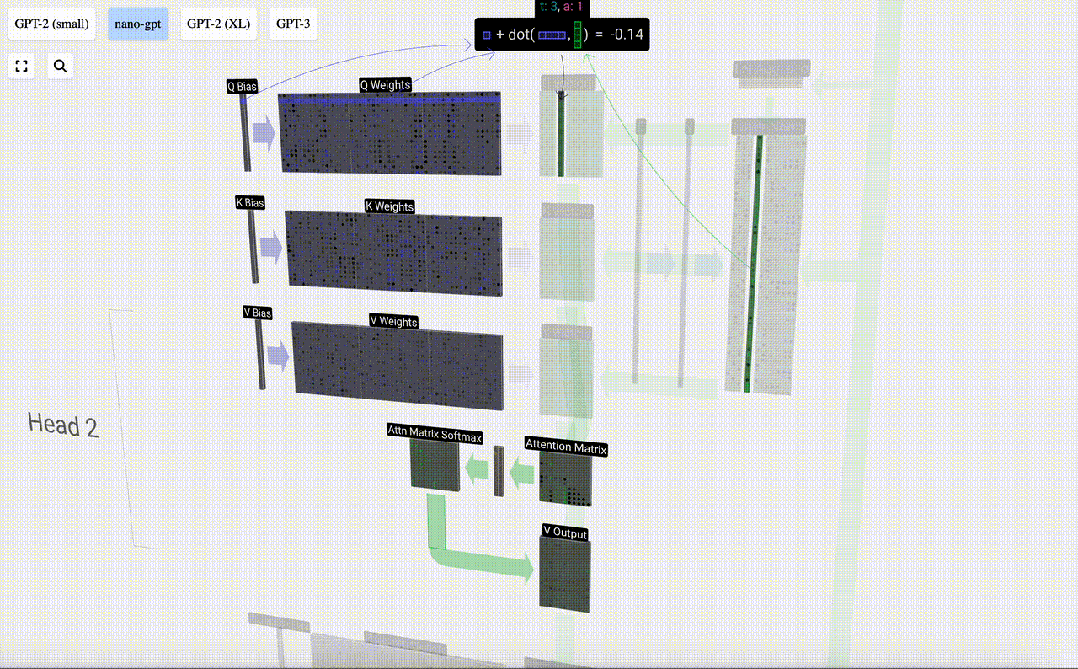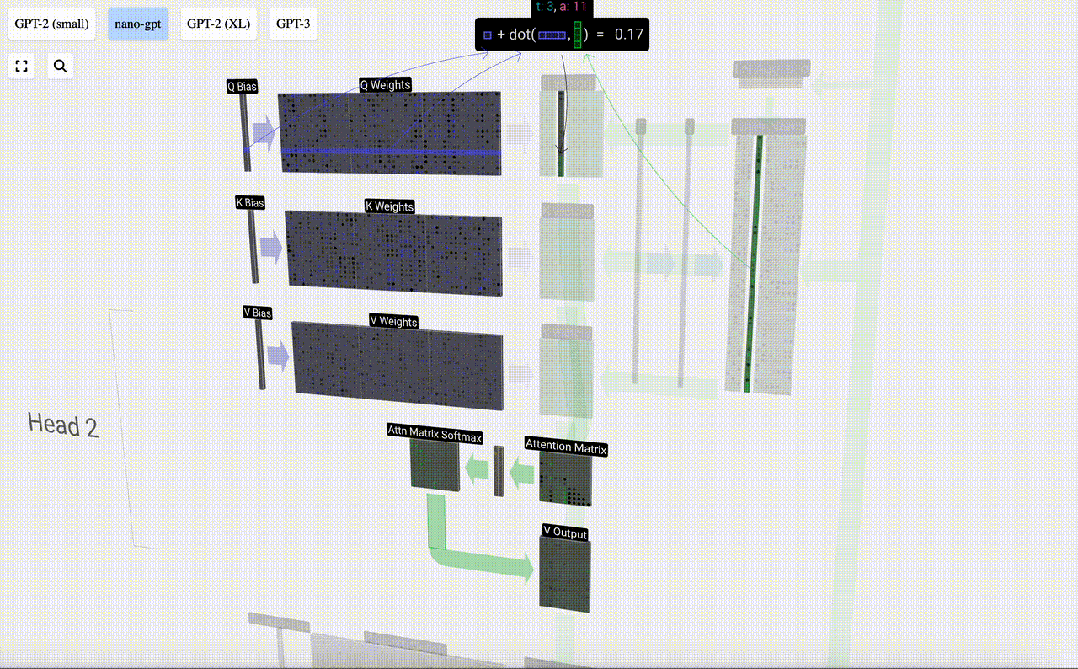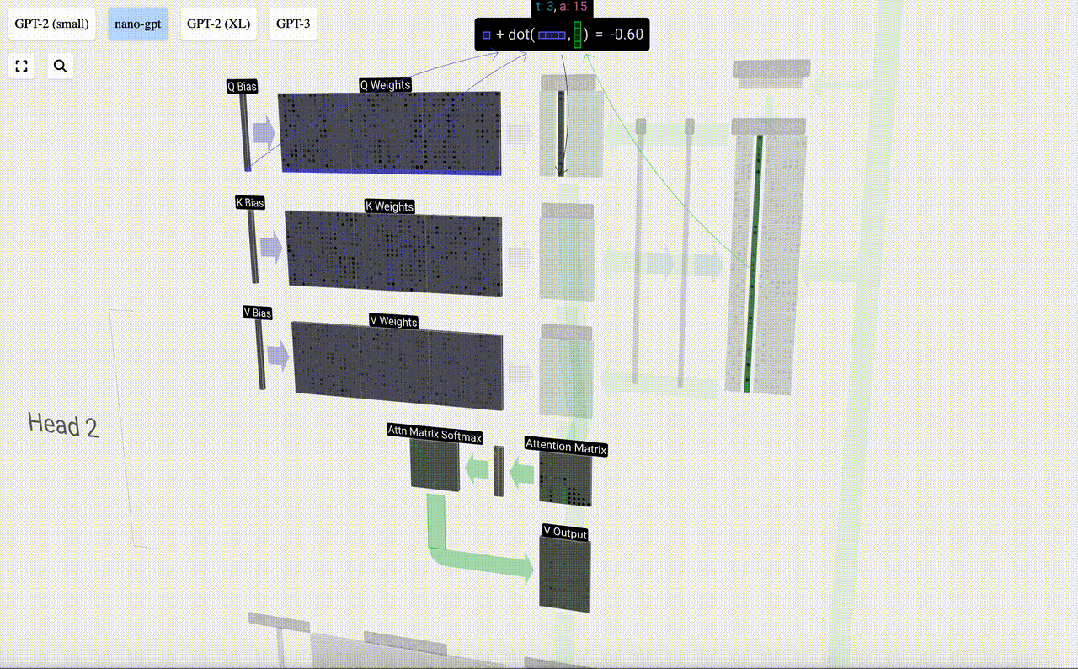
每個輸出單元都是輸入向量的線性組合。例如,對于Q向量,這是用Q權重矩陣的一行和輸入矩陣的一列之間的點積來完成的。
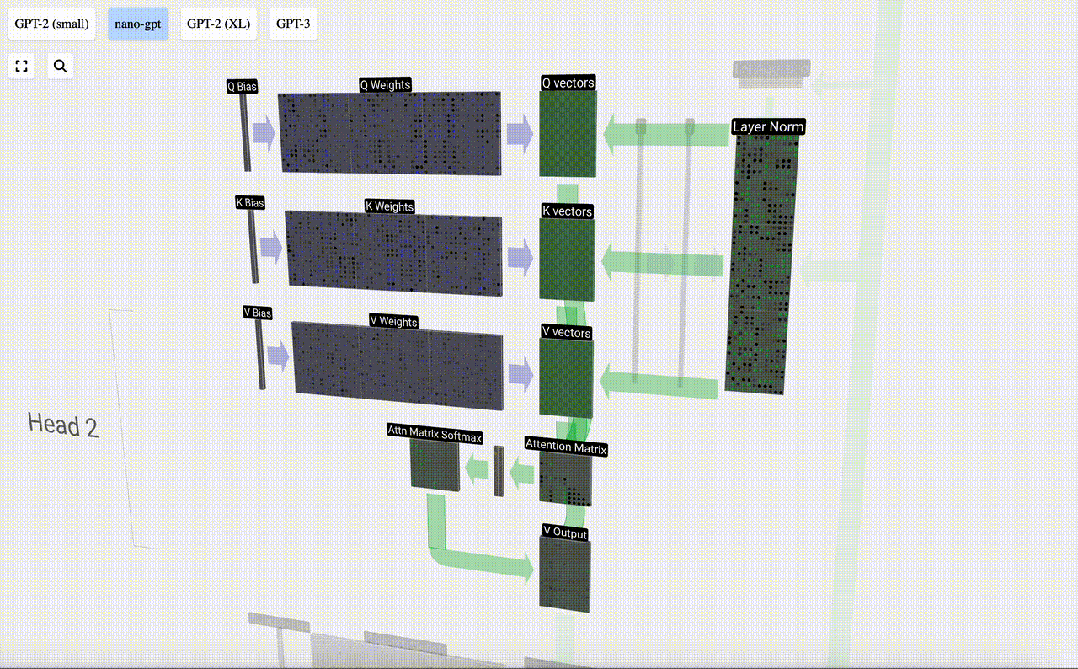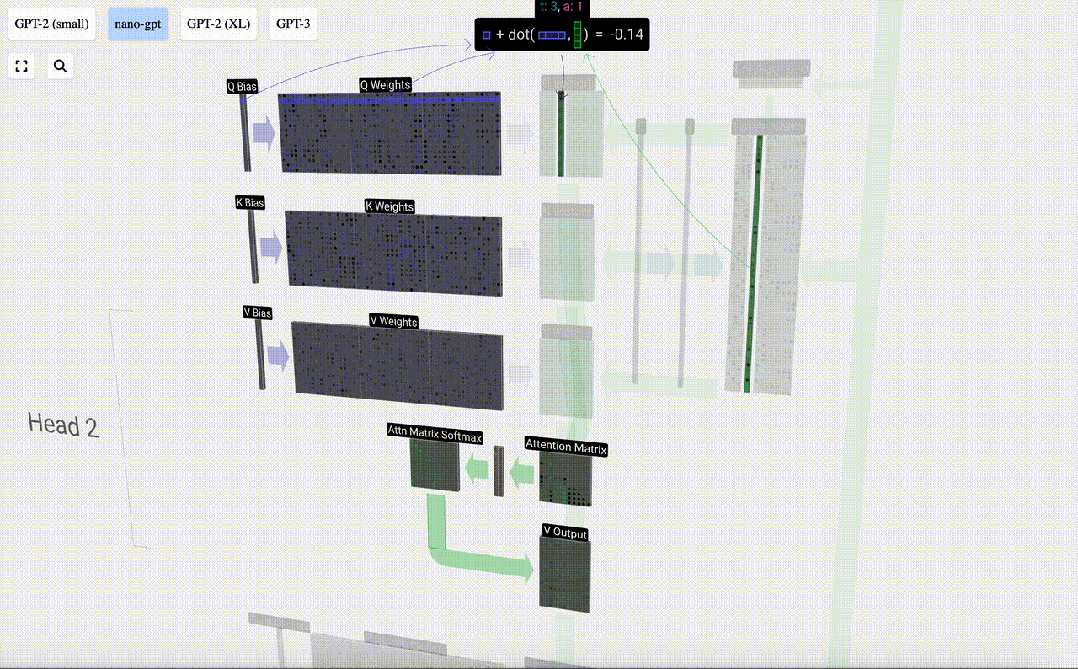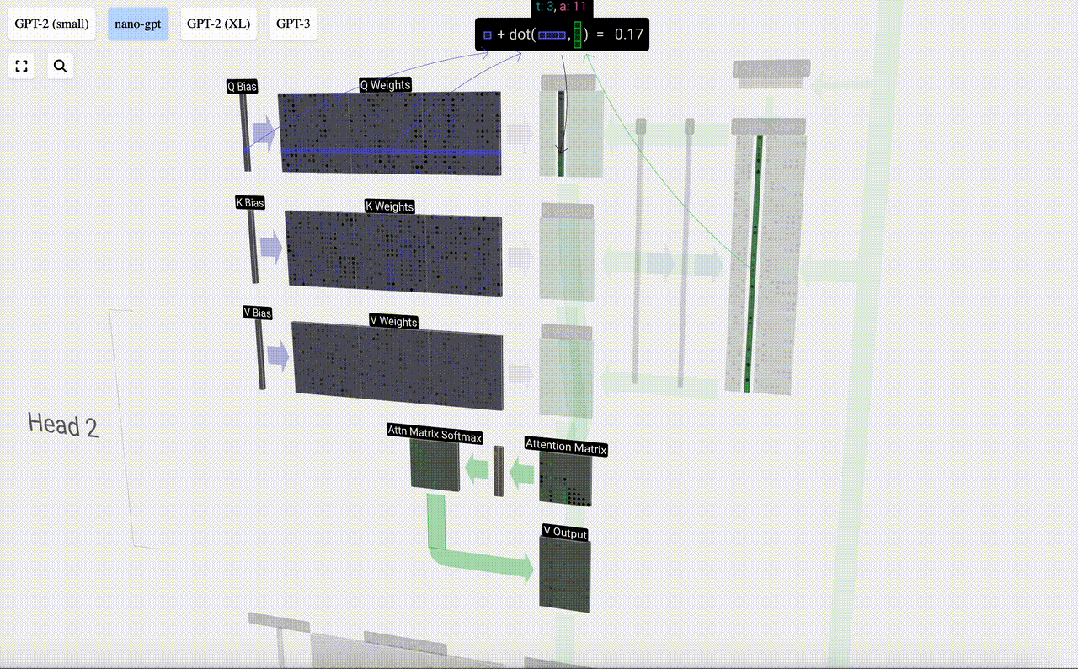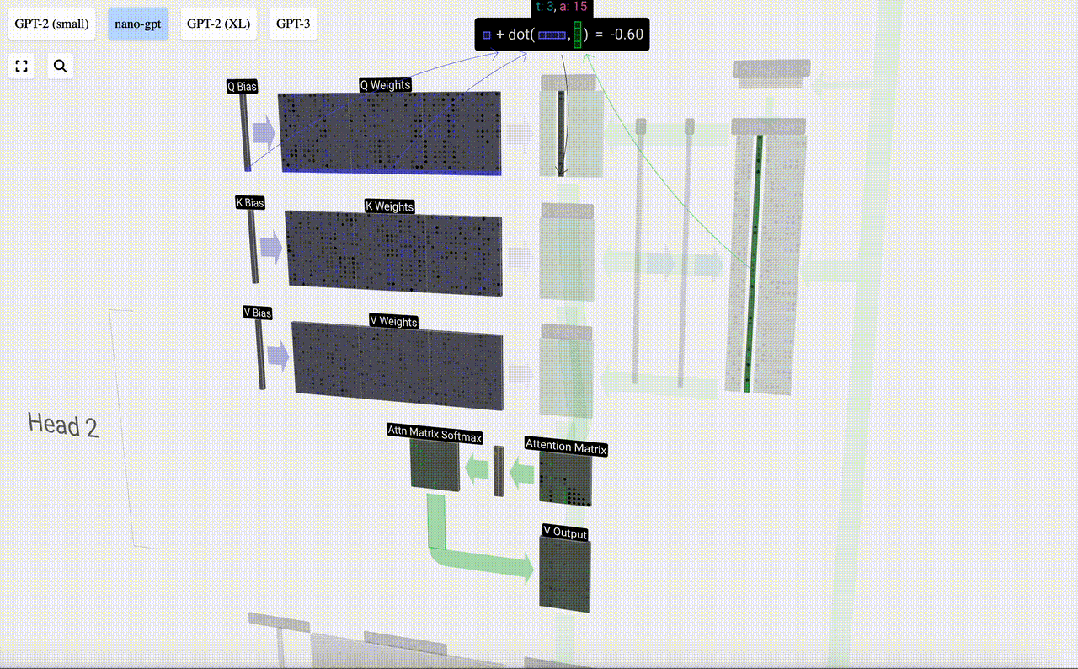 圖片
圖片
我們會經常看到的點乘運算非常簡單:我們將第一個向量中的每個元素與第二個向量中的相應元素配對,將這對元素相乘,然后將結果相加。
 圖片
圖片
這是一種確保每個輸出元素都能受到輸入向量中所有元素影響的通用而簡單的方法(這種影響由權重決定)。因此,它經常出現在神經網絡中。
我們對Q、K、V向量中的每個輸出單元重復這一操作:
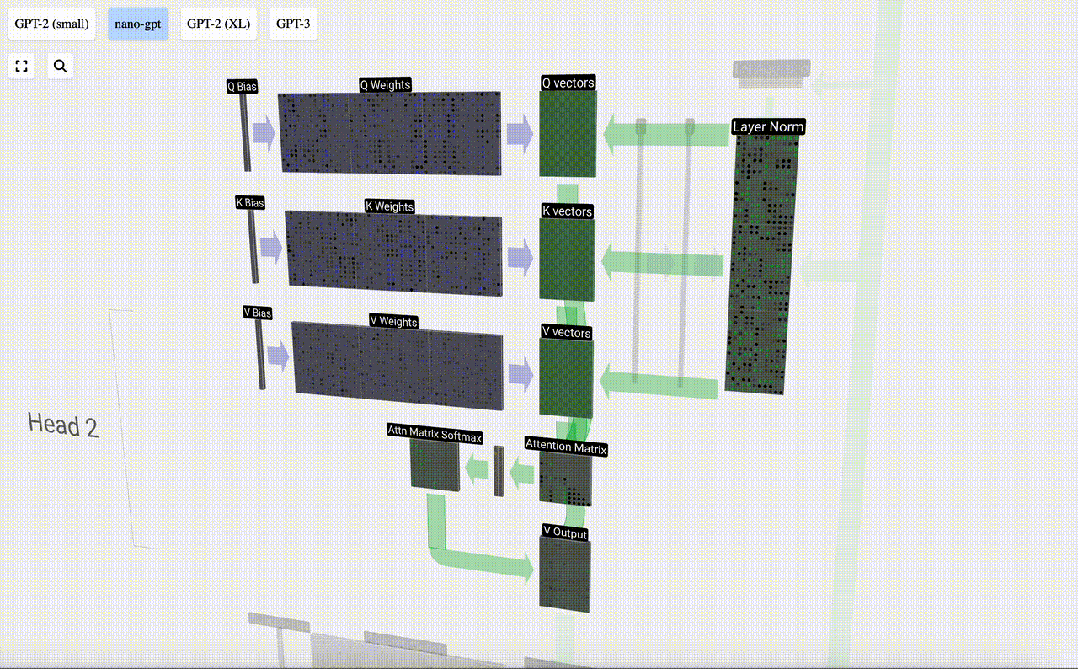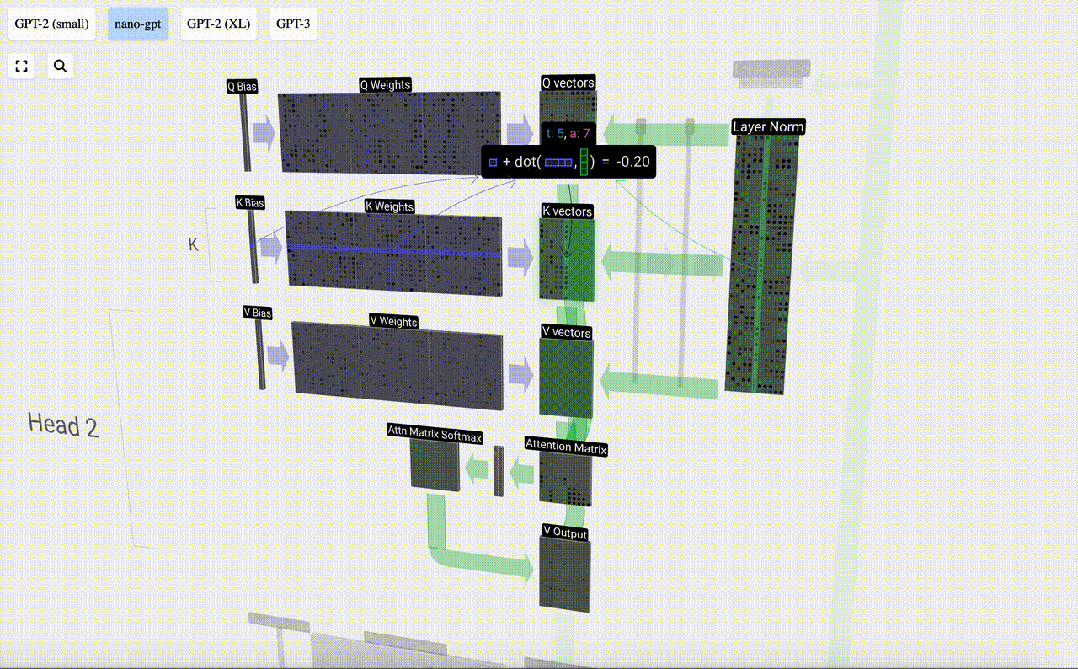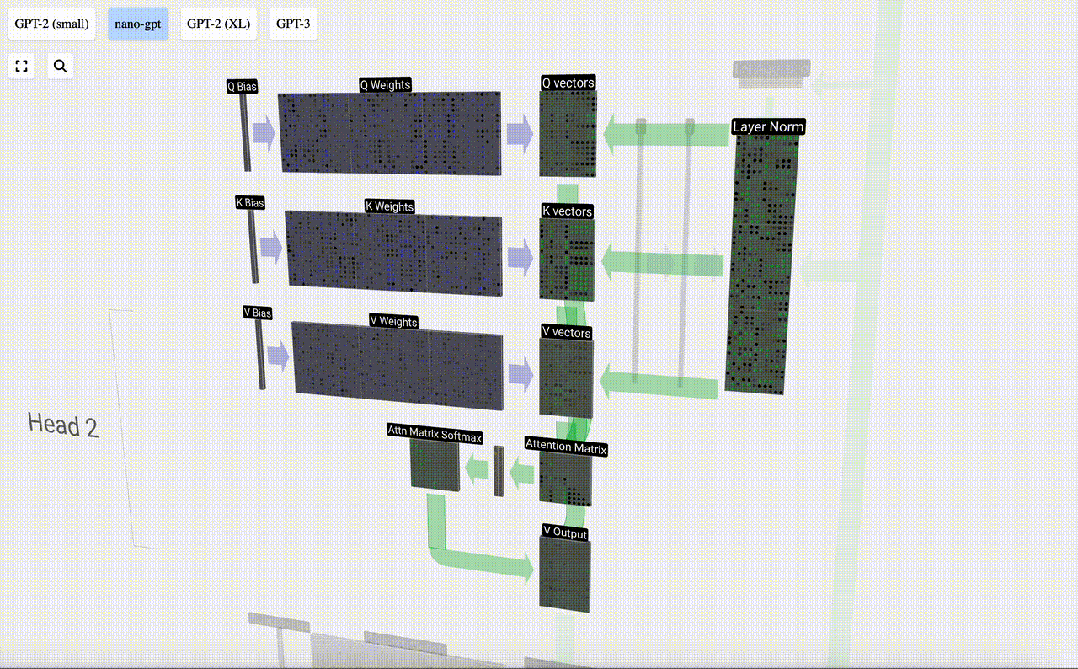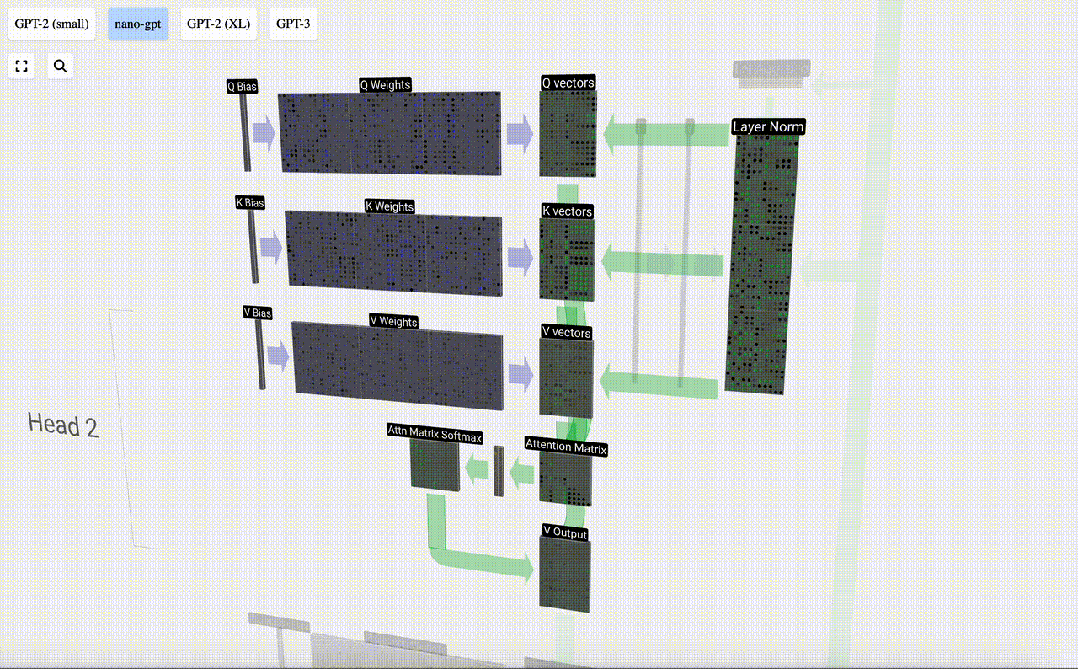 圖片
圖片
我們該如何處理Q、K和V向量呢?命名給了我們一個提示:「key」和「value」讓人聯想到軟件中的字典,
鍵(key)映射到值(value)。然后「query」就是我們用于查找值的東西。
 圖片
圖片
在自注意力的情況下,我們返回的不再是單個詞條,而是詞條的加權組合。
為了找到這個加權,我們在Q向量和K向量之間進行點乘。我們將加權歸一化,最后用它與相應的V向量相乘,再將它們相加。
 圖片
圖片
舉個更具體的例子,讓我們看看第6列(t=5),我們將從這一列開始查詢:
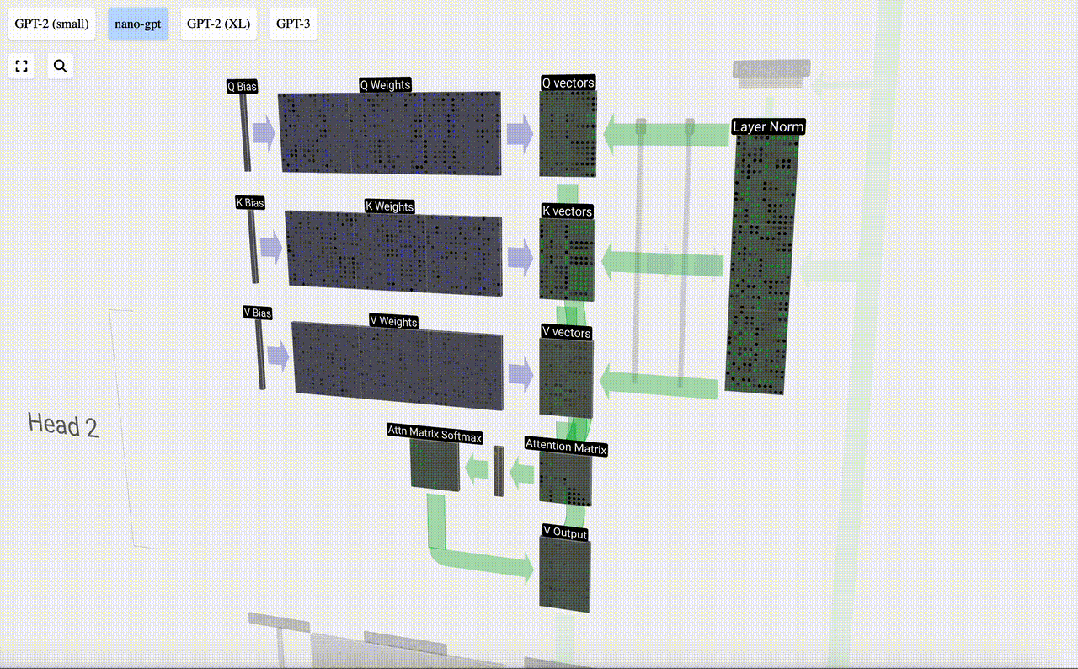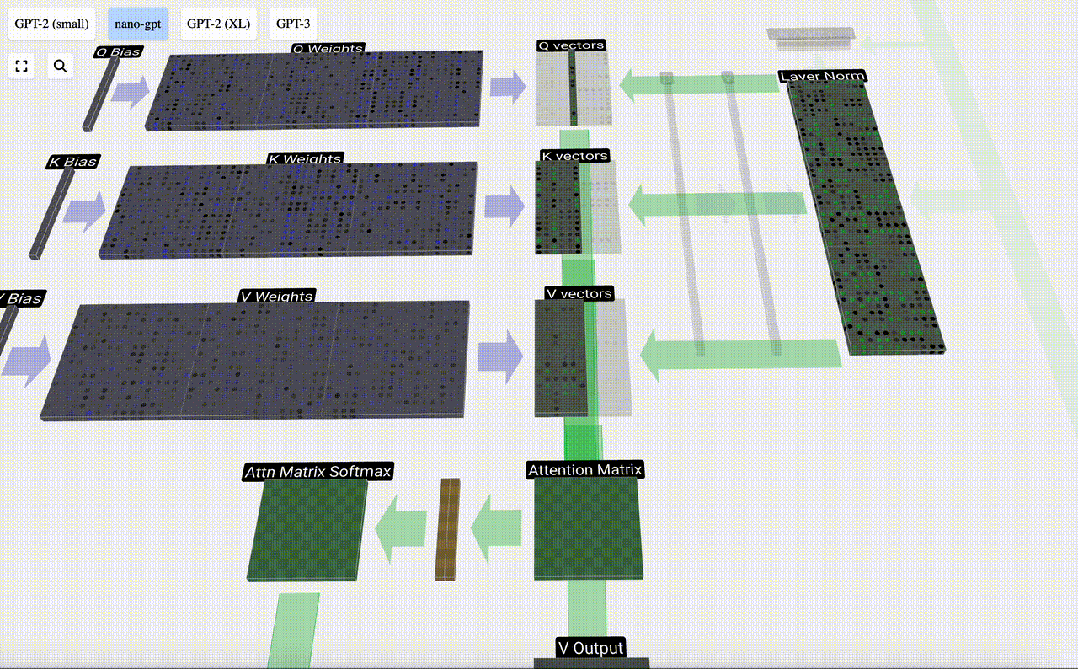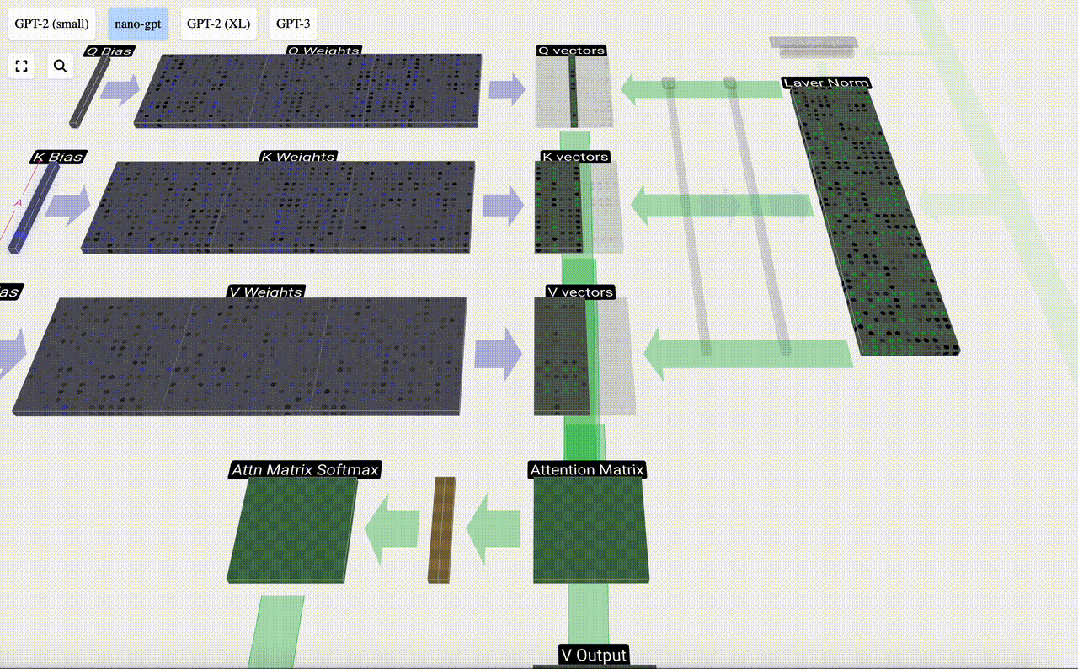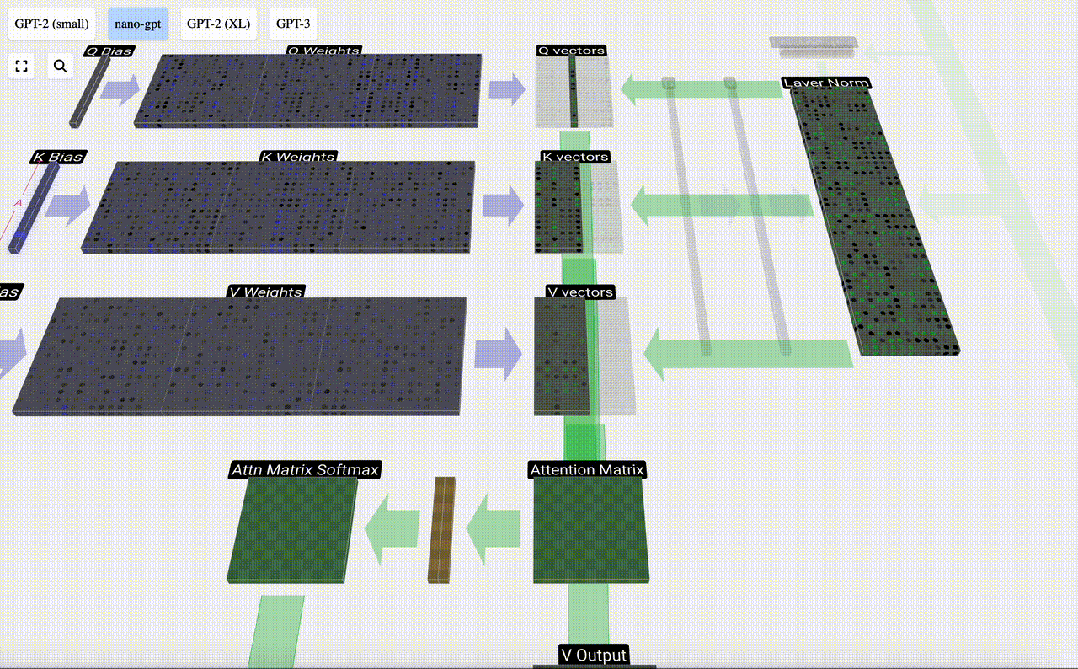 圖片
圖片
我們查找的 {K, V} 項是過去的6列,Q值是當前時間。
我們首先計算當前列(t=5)的Q向量與之前各列的K向量之間的點積。然后將其存儲在注意力矩陣的相應行(t=5)中。
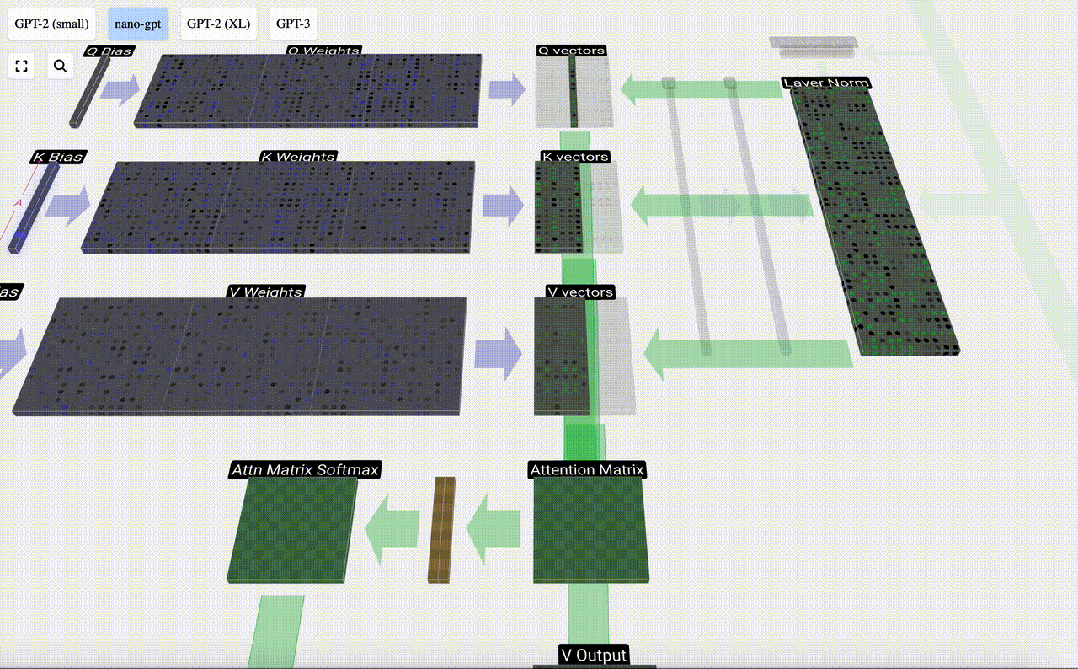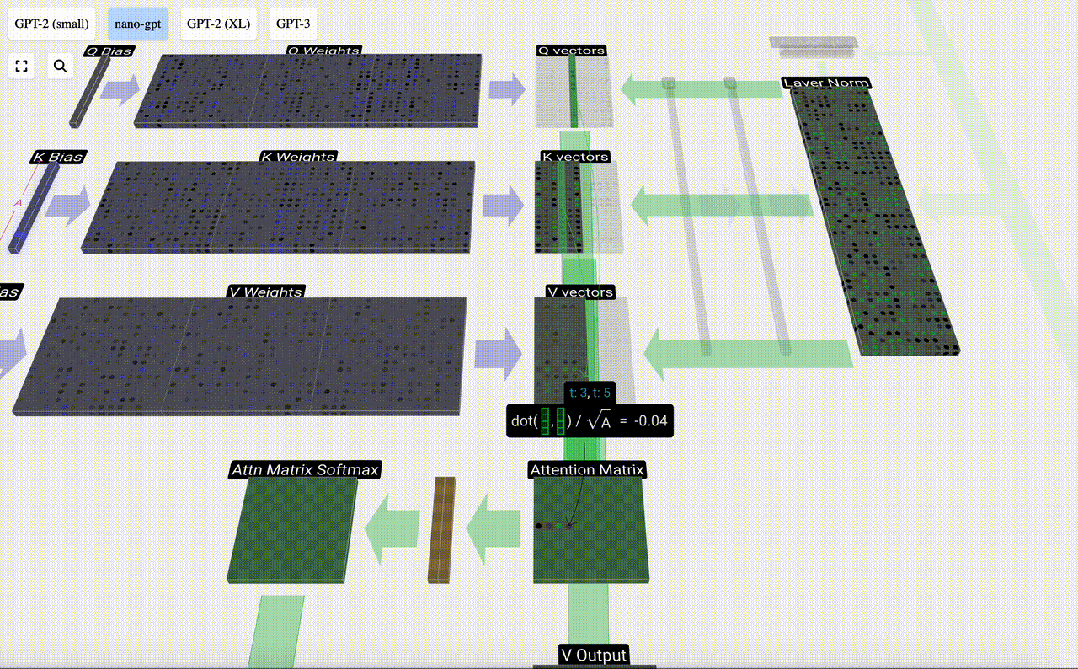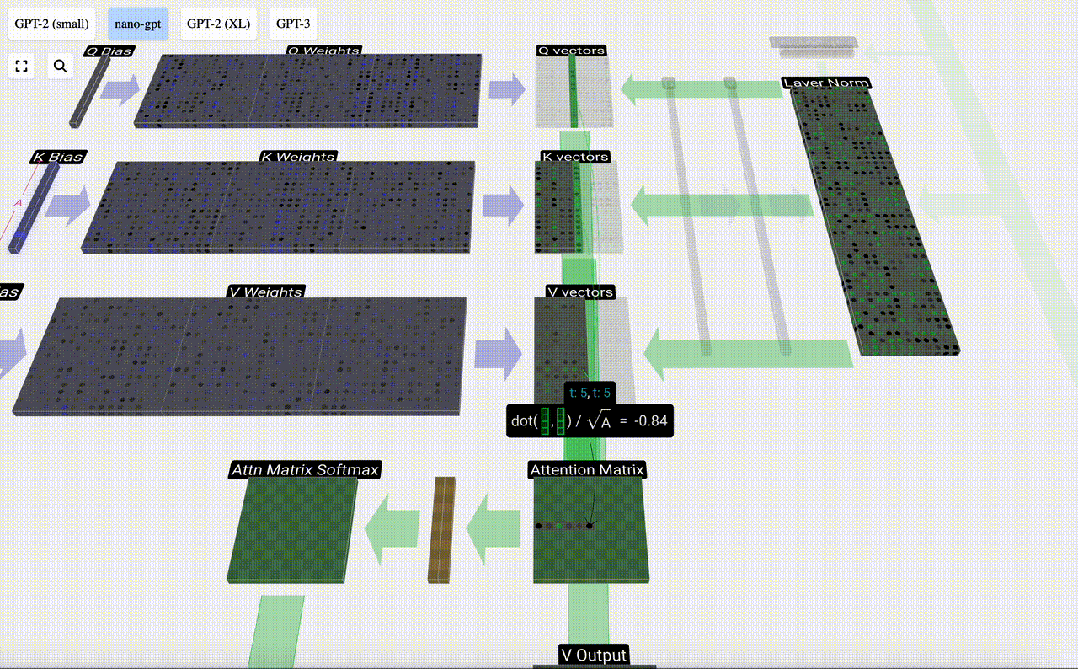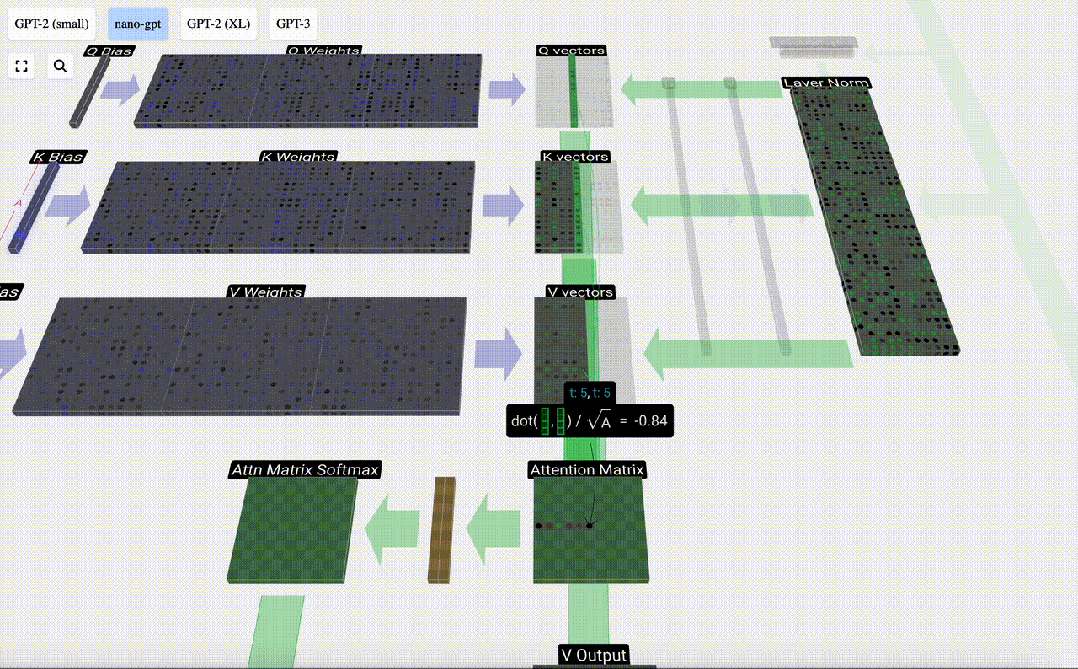 圖片
圖片
這些點積是衡量兩個向量相似度的一種方法。如果它們非常相似,點積就會很大。如果兩個向量非常不同,點積就會很小或為負。
只將query向量與過去的key向量進行運算,使得它成為因果自注意力。也就是說,token無法「預見未來」。
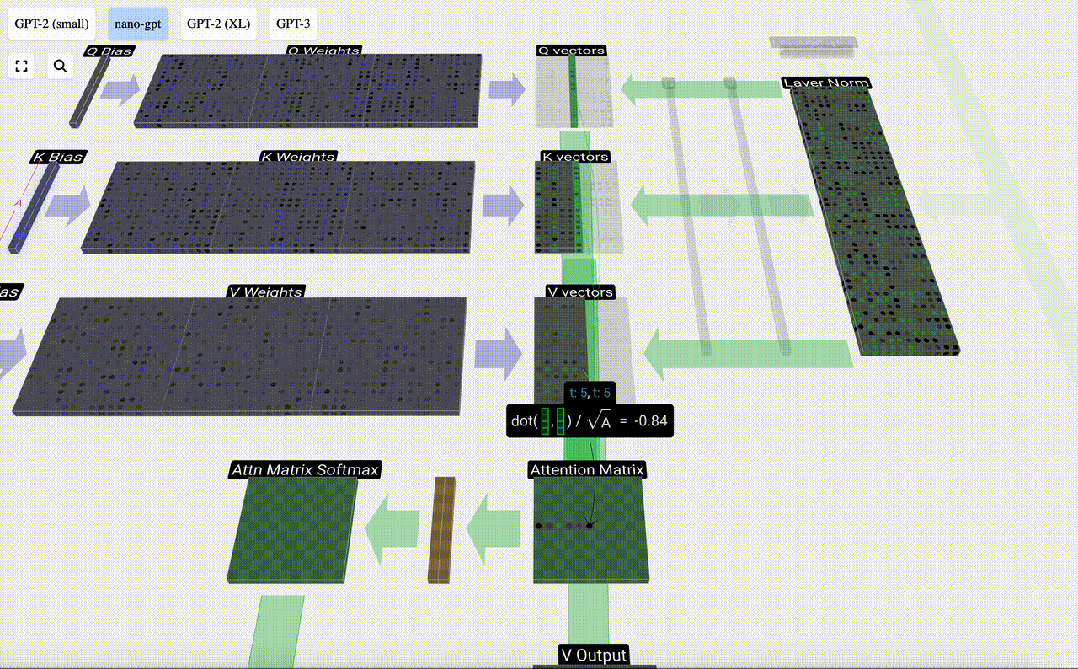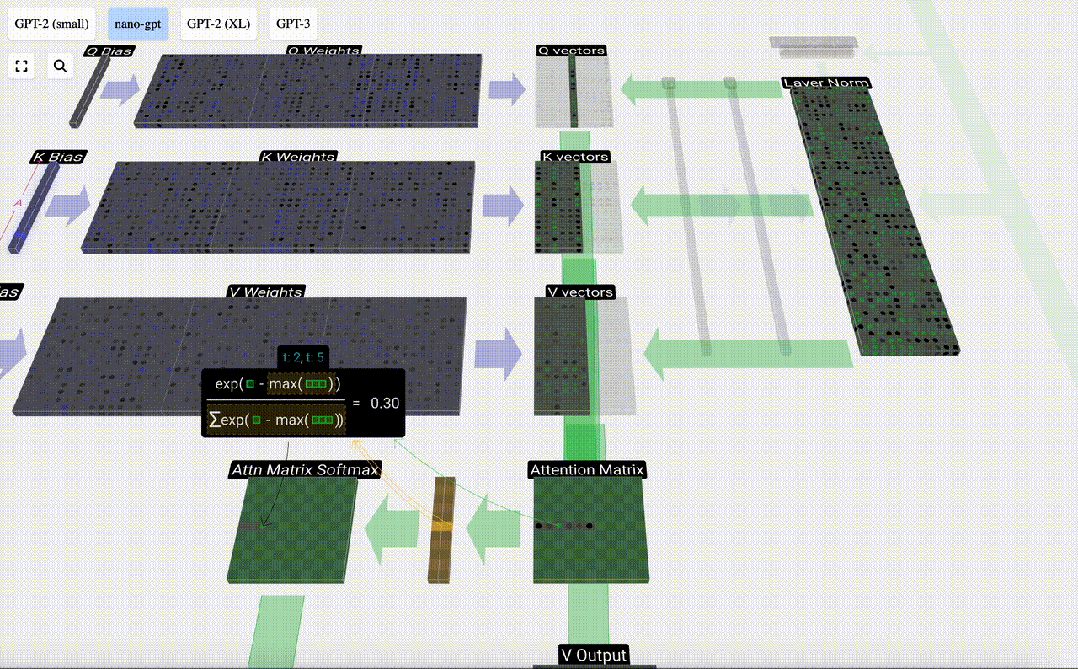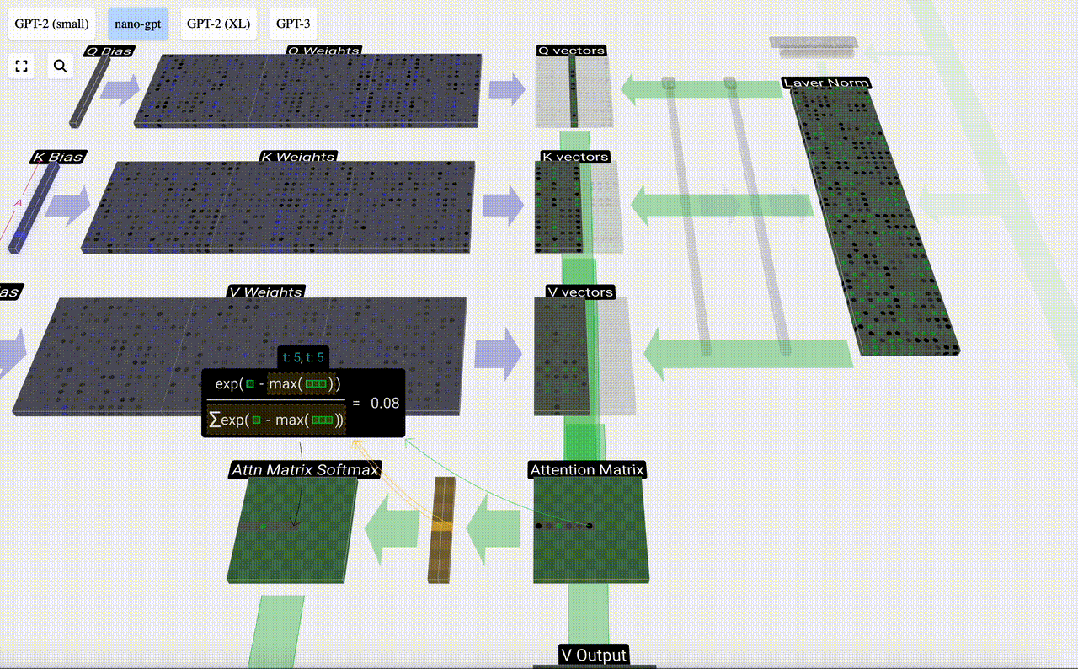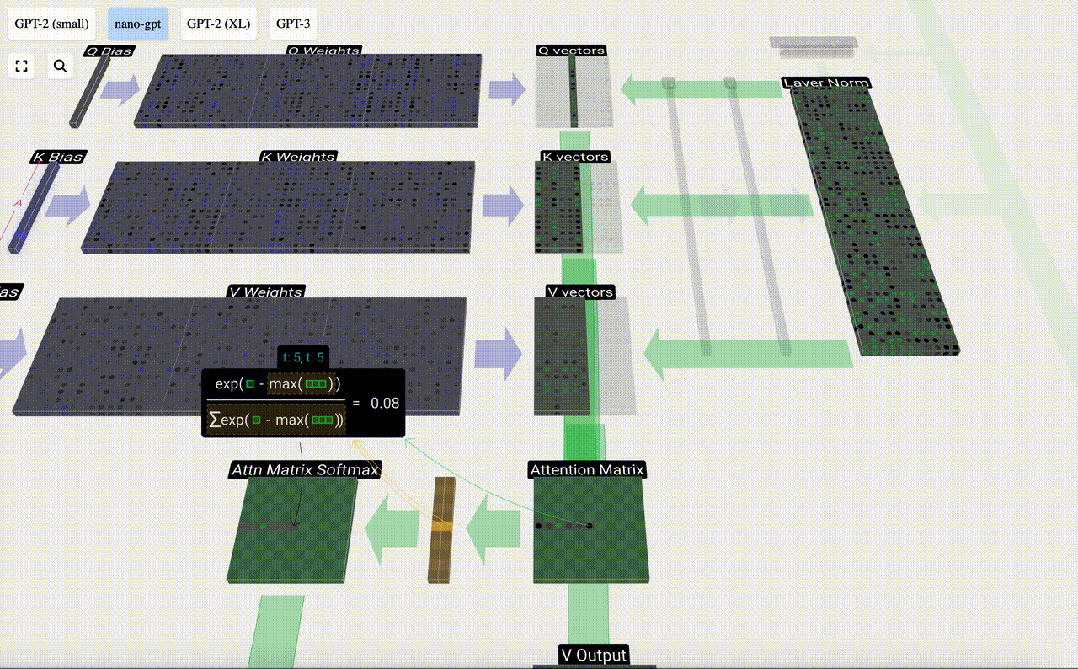
另一個要素是,在求出點積后,我們要除以sqrt(A),其中A是Q/K/V向量的長度。進行這種縮放是為了防止大值在下一步的歸一化(softmax)中占主導地位。
我們將跳過softmax操作(稍后解釋),只需說明每一行的歸一化總和為1即可。
 圖片
圖片
最后,我們就可以得出這一列(t=5)的輸出向量。我們查看歸一化自注意力矩陣的(t=5)行,并將每個元素與其他列的相應V向量相乘。
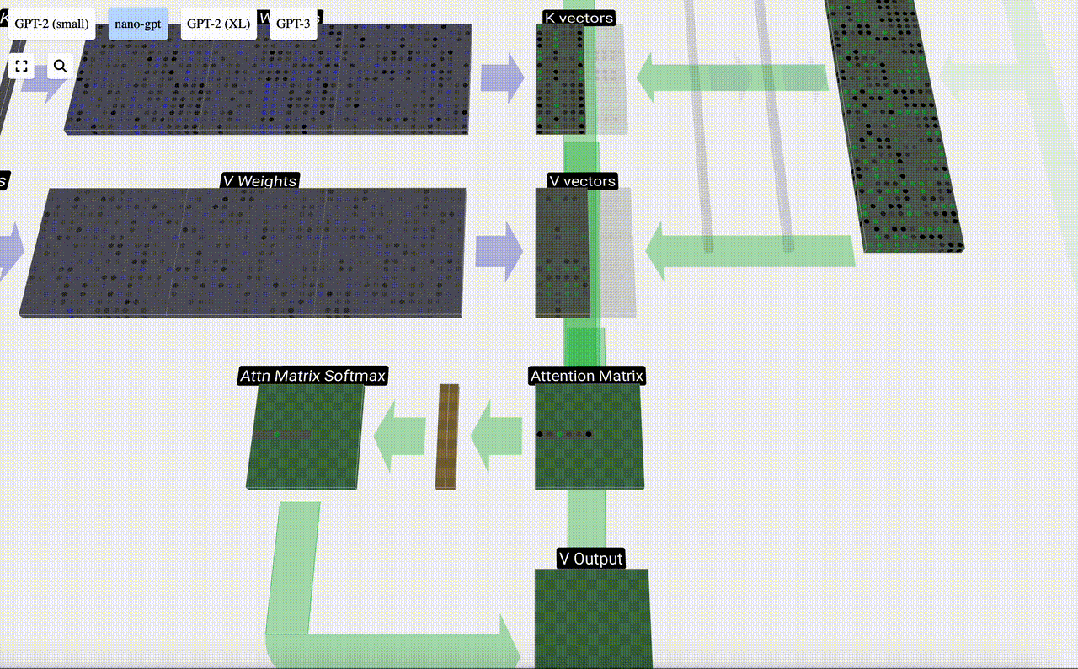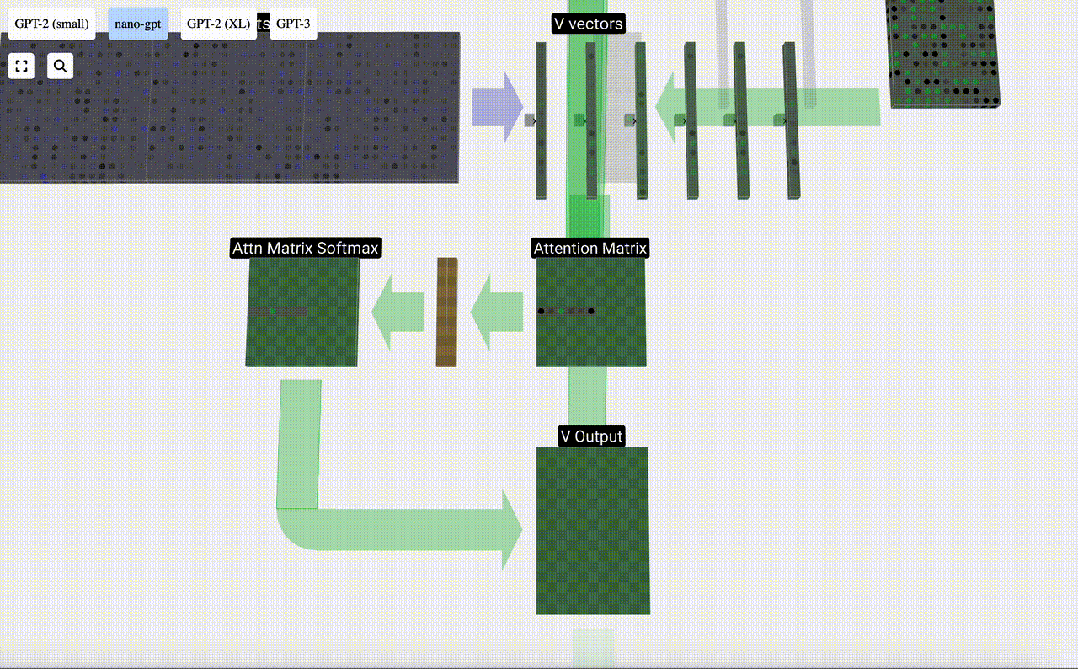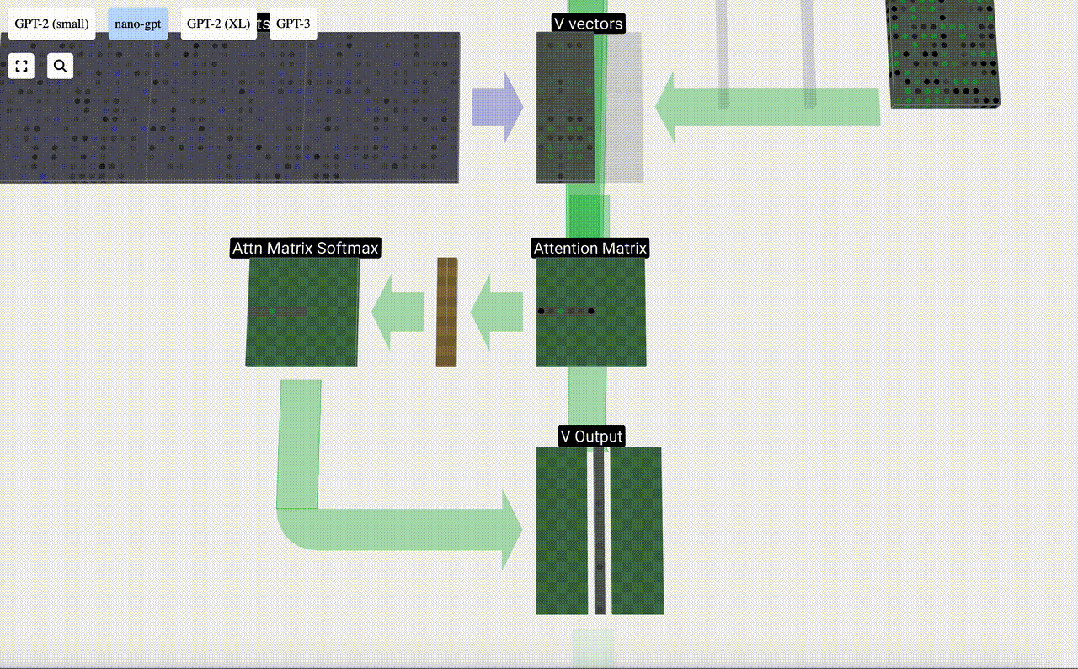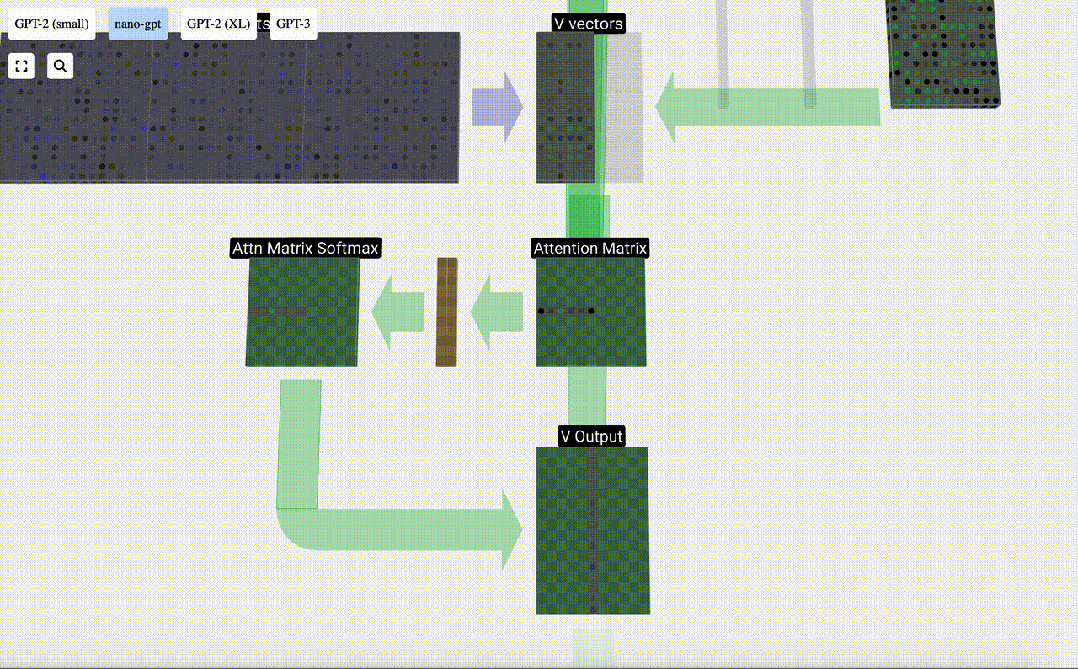 圖片
圖片
然后,我們可以將這些向量相加,得出輸出向量。因此,輸出向量將以高分列的V向量為主。
現在我們知道了這個過程,讓我們對所有列進行運行。
這就是自注意力層中的一個頭的處理過程。
所以自注意力的主要目標是,每個列向量希望從其他列向量中找到相關信息,提取它們的值,方法是將其查詢向量與其他列向量的鍵值進行比較。但有一個附加限制,即它只能查找過去的信息。
投影
在自我注意力過程之后,我們會從每個頭得到一個輸出。這些輸出是受Q和K向量影響而適當混合的V向量。
要合并每個頭的輸出向量,我們只需將它們堆疊在一起即可。因此,在時間t=4時,我們將從3個長度為A=16的向量疊加到1個長度為C=48的向量。
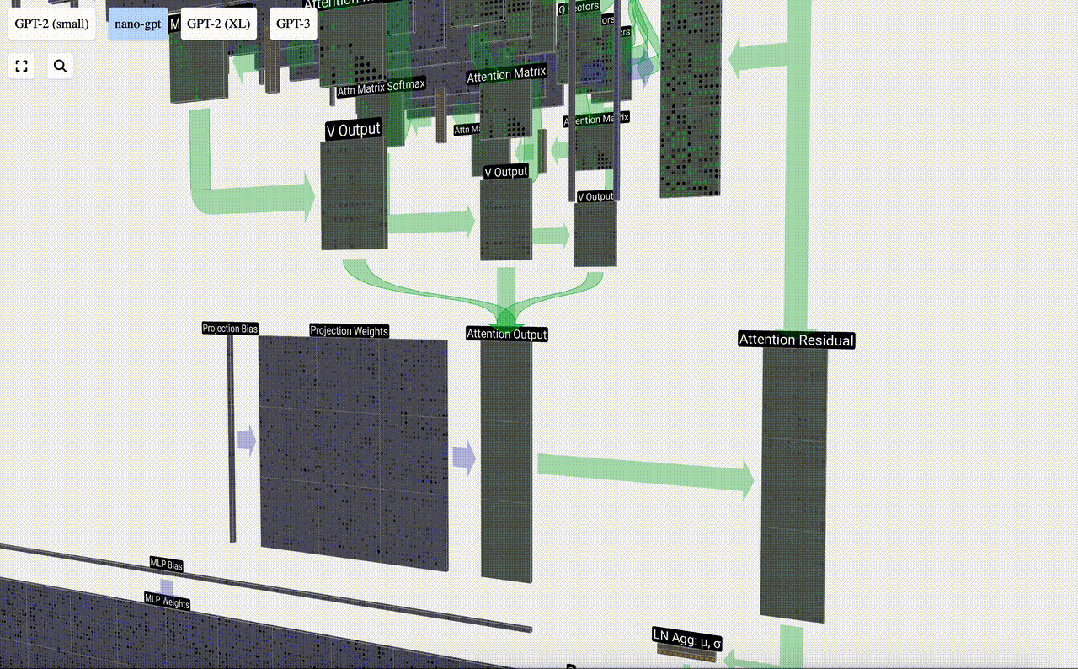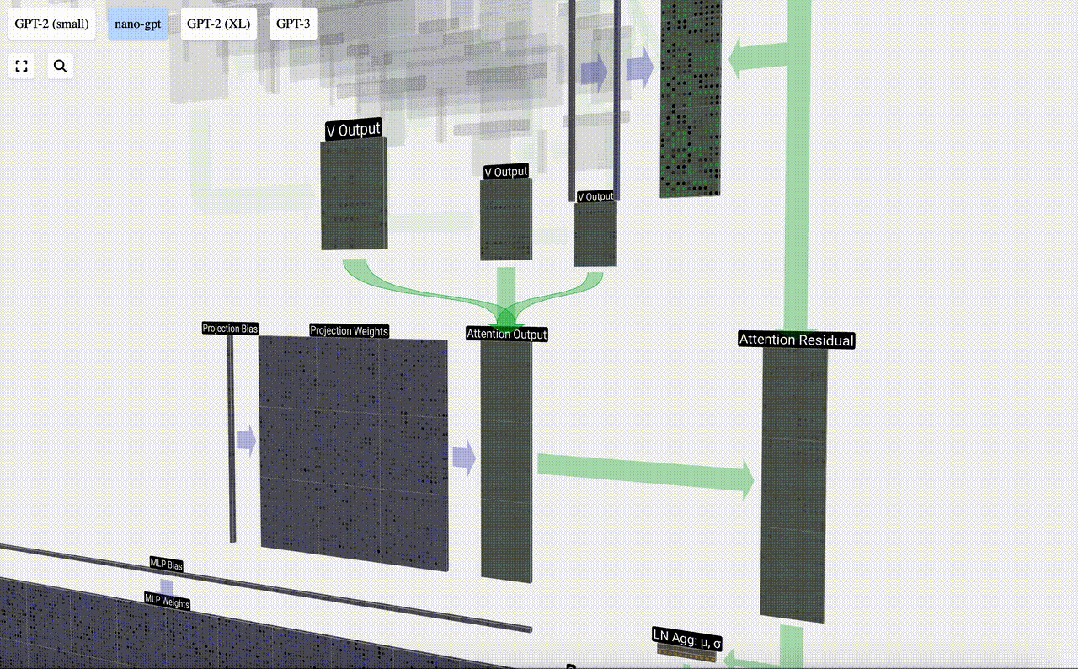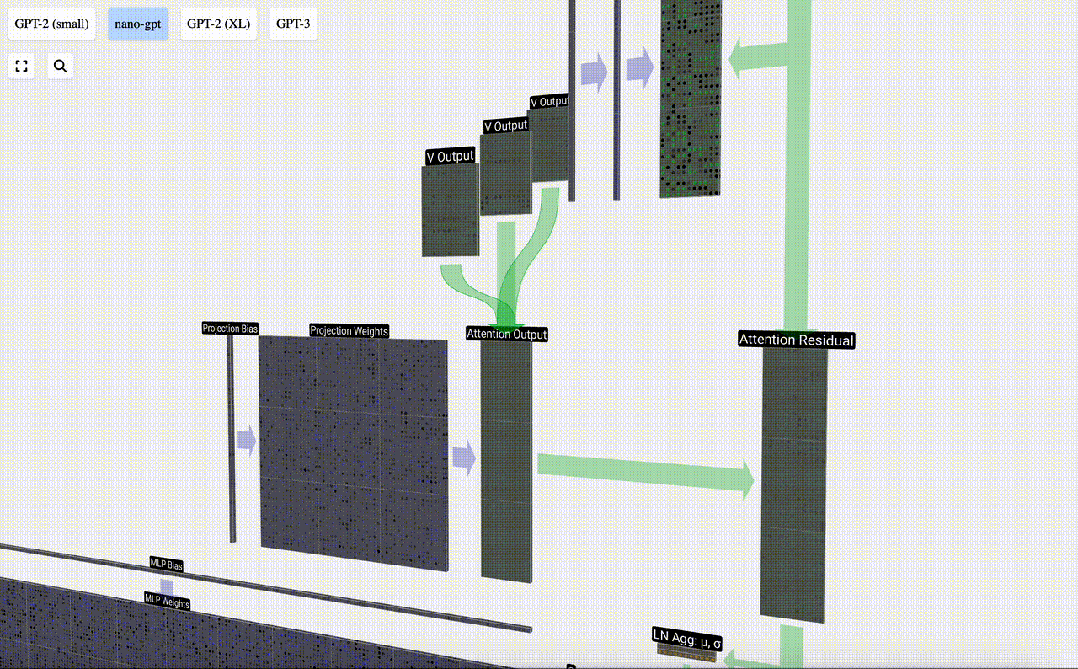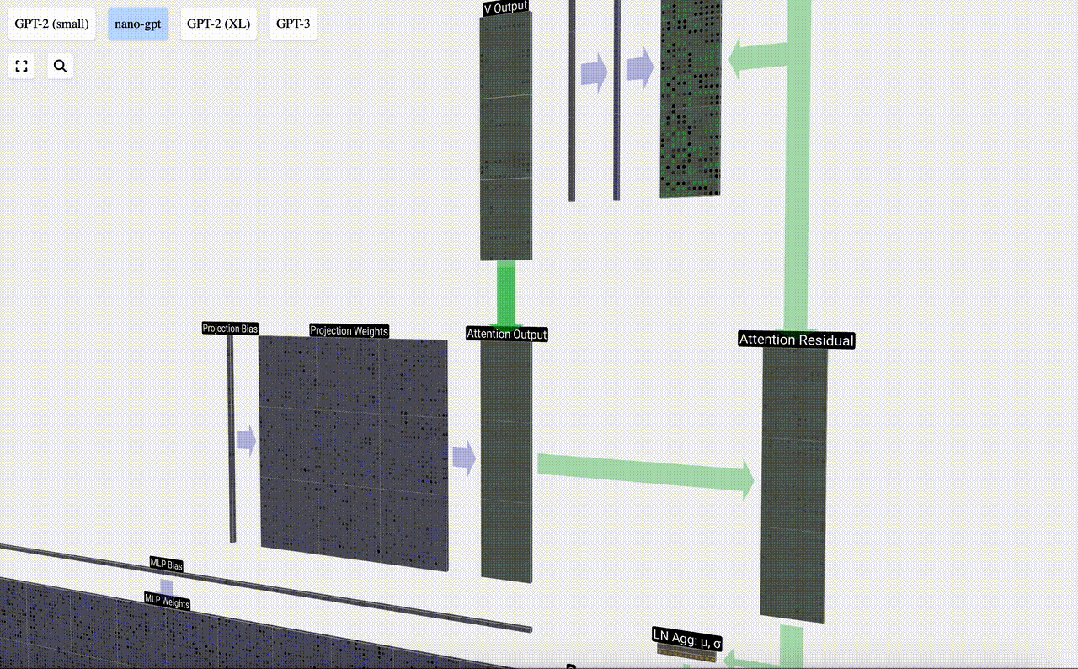 圖片
圖片
值得注意的是,在GPT中,頭(A=16)內向量的長度等于 C/num_heads。這確保了當我們將它們重新堆疊在一起時,能得到原來的長度C。
在此基礎上,我們進行投影,得到該層的輸出。這是一個簡單的矩陣-向量乘法,以每列為單位,并加上偏置。
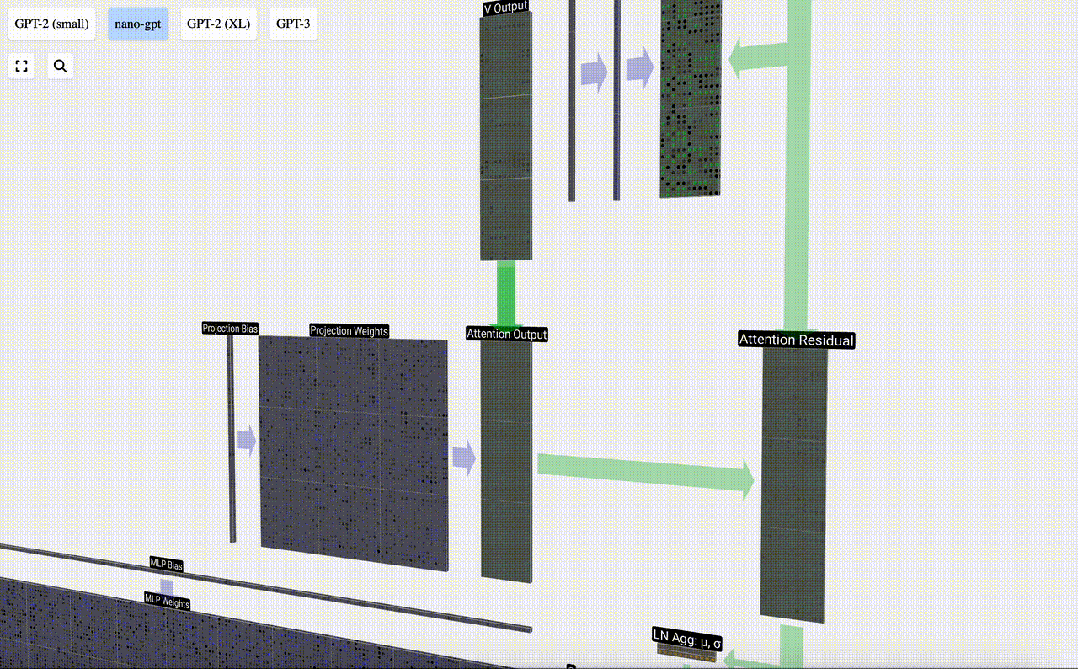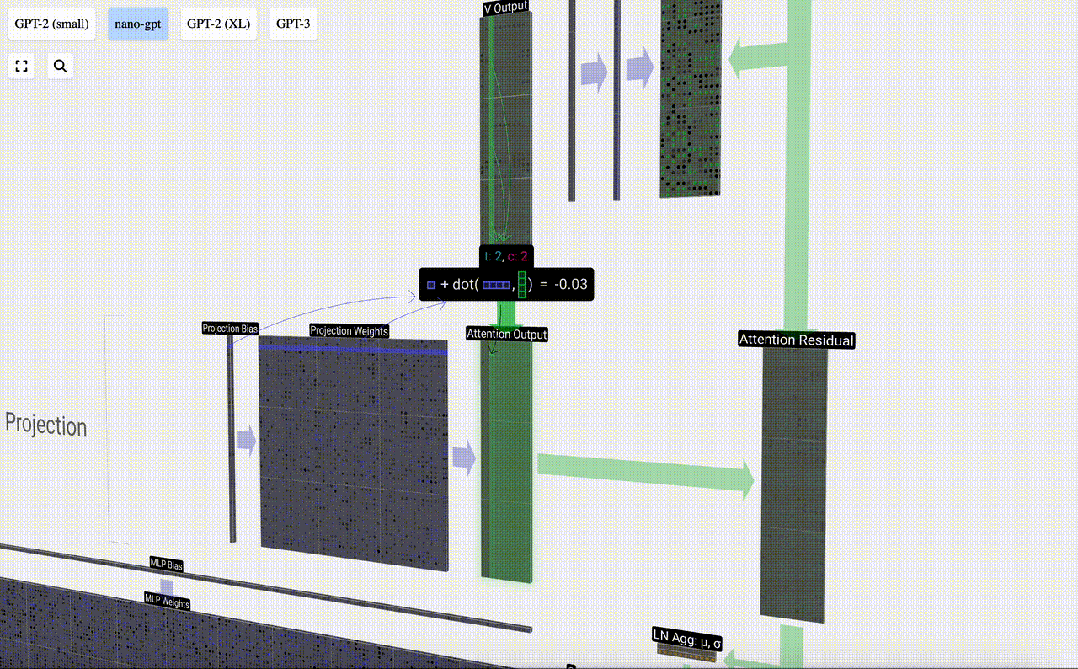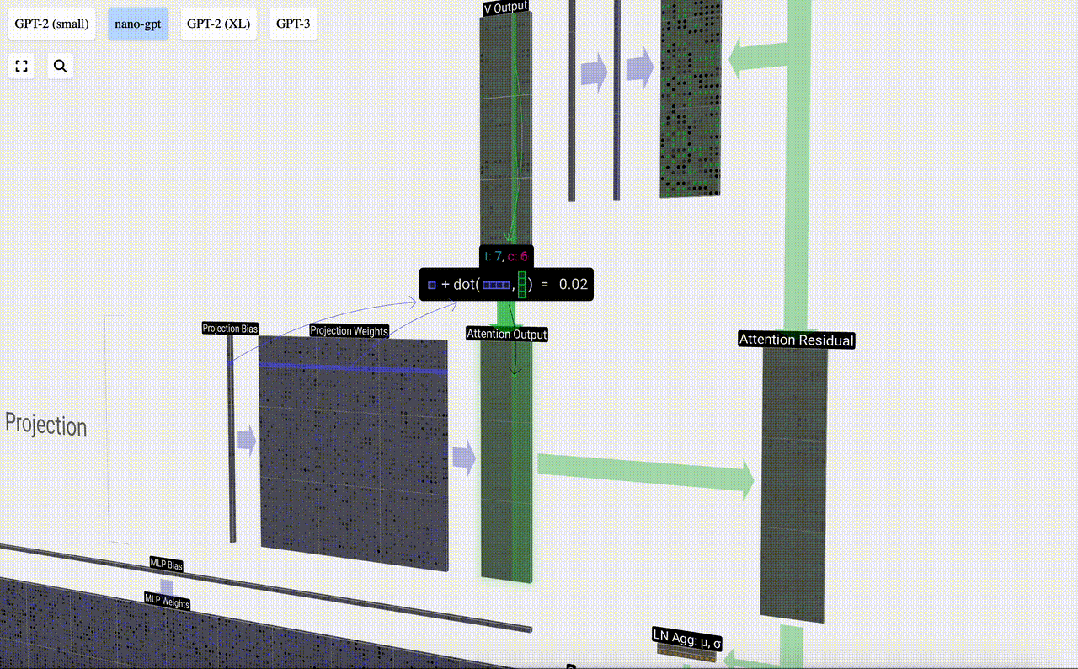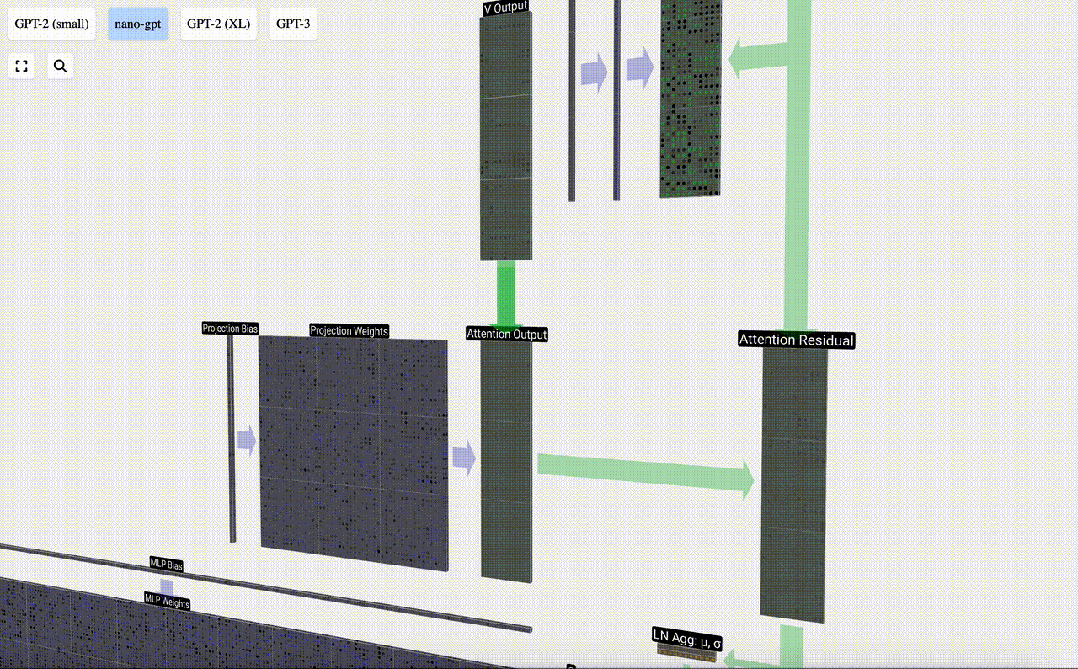 圖片
圖片
現在,我們得到了自注意力層的輸出結果。
我們不會直接將這一輸出傳遞到下一階段,而是將其按元素順序添加到輸入嵌入中。綠色垂直箭頭表示的這一過程被稱為殘差連接(residual connection)或殘差路徑(residual pathway)。
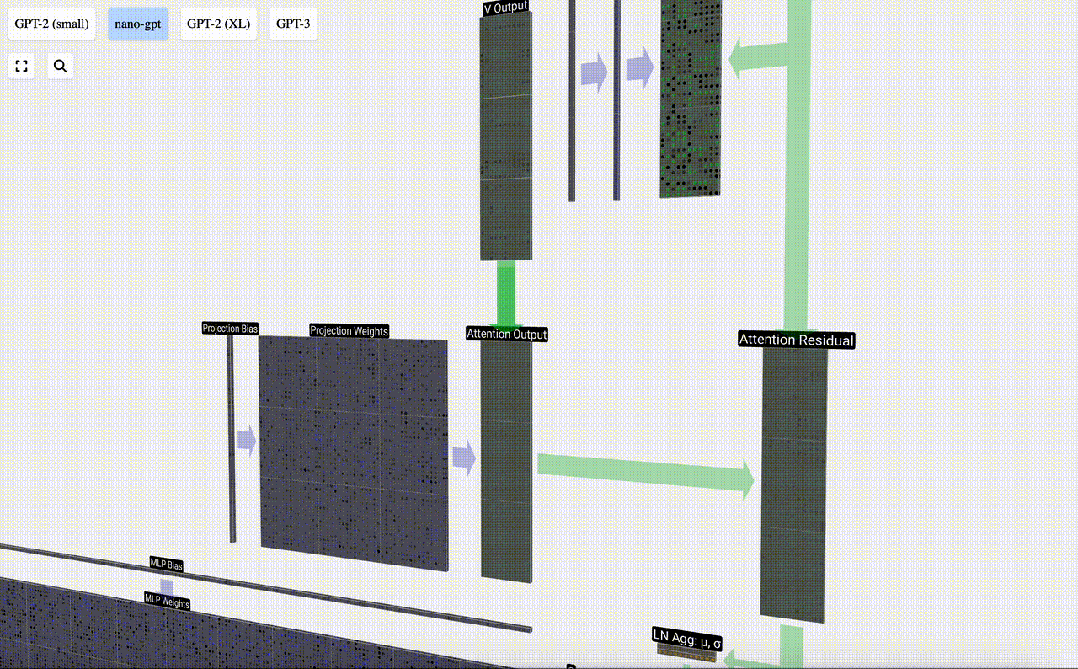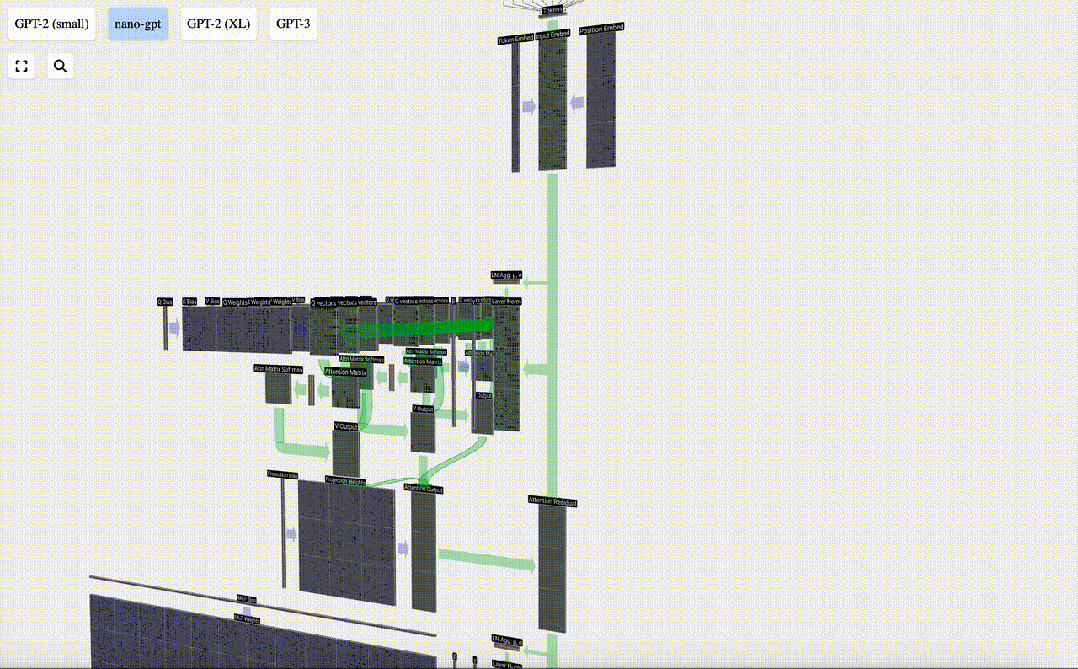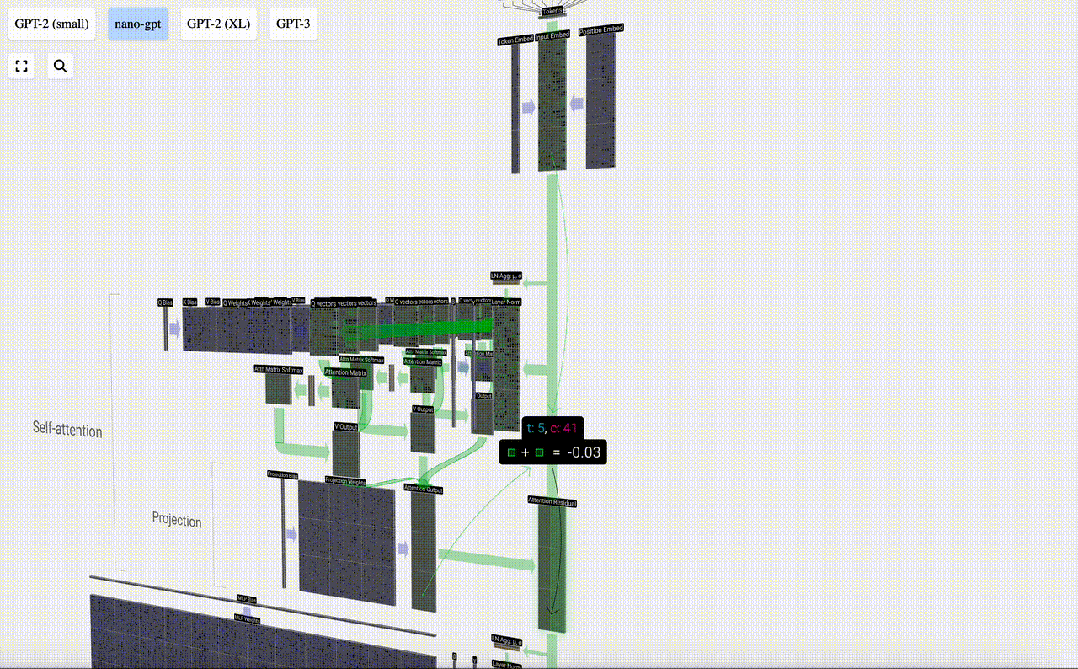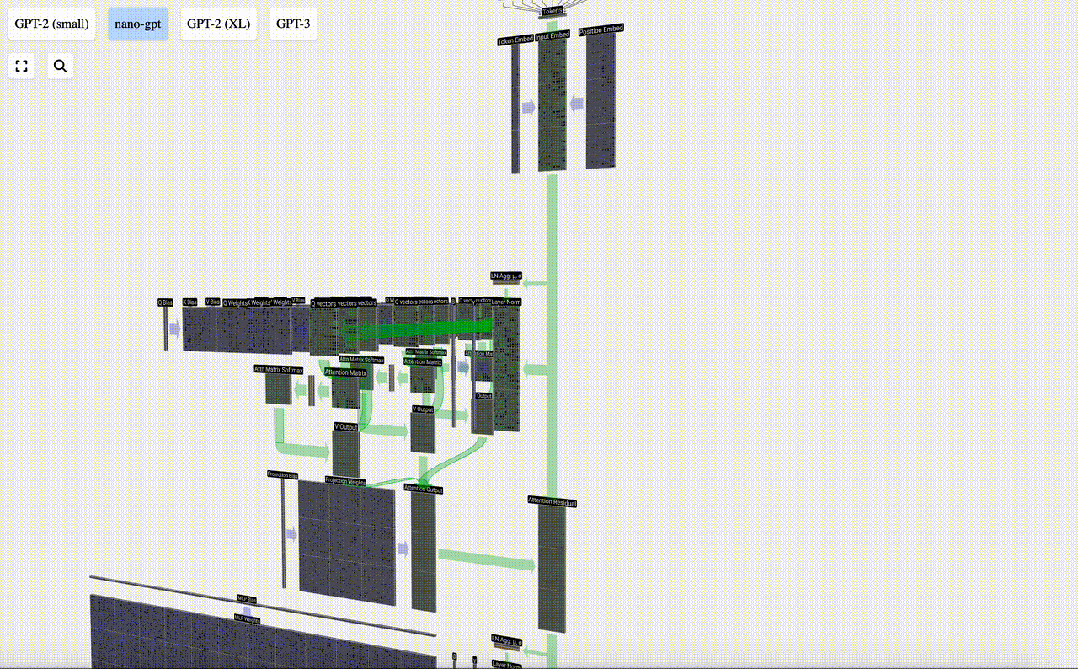 圖片
圖片
與「層歸一化」一樣,殘差路徑對于實現深度神經網絡的有效學習非常重要。
有了自注意力的結果,我們就可以將其傳遞到Transformer的下一個部分:前饋神經網絡。
MLP
在自注意力層之后,Transformer模塊的下半部分是MLP(多層感知器)。雖然有點拗口,但在這里它是一個有兩層的簡單神經網絡。
與自注意力一樣,在向量進入MLP之前,我們要進行層歸一化處理。
在MLP中,我們將每個長度為C=48的列向量(獨立地)進行以下處理:
1. 添加偏置的線性變換,轉換為長度為4*C的向量。
2. 一個GELU激活函數(按元素計算)
3. 進行線性變換并添加偏置,返回長度為C的向量
讓我們追蹤其中一個向量:
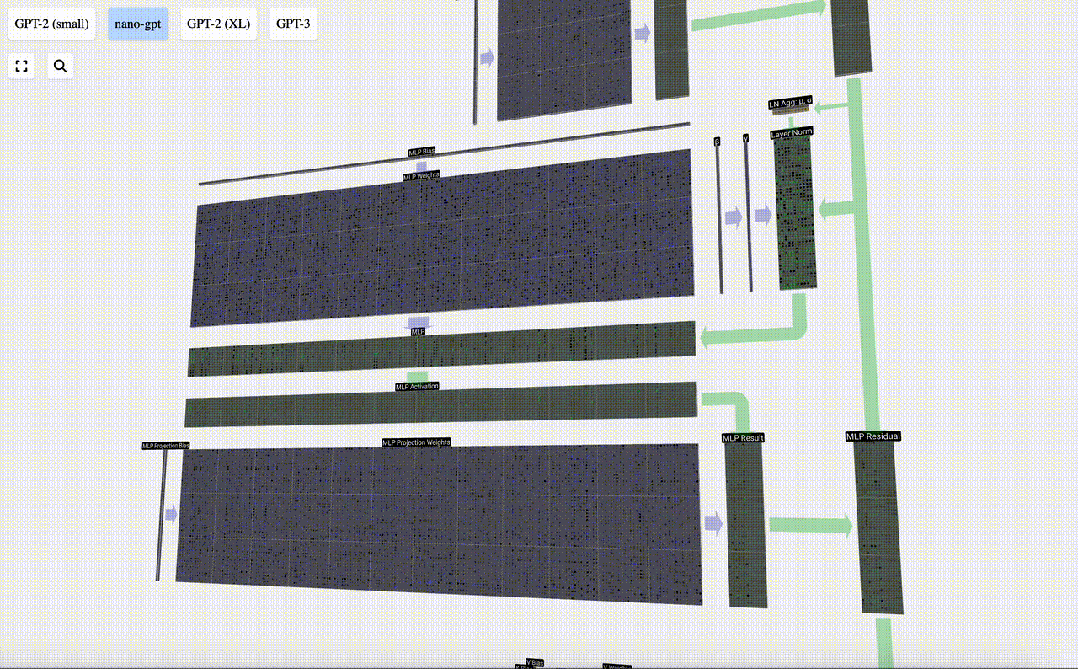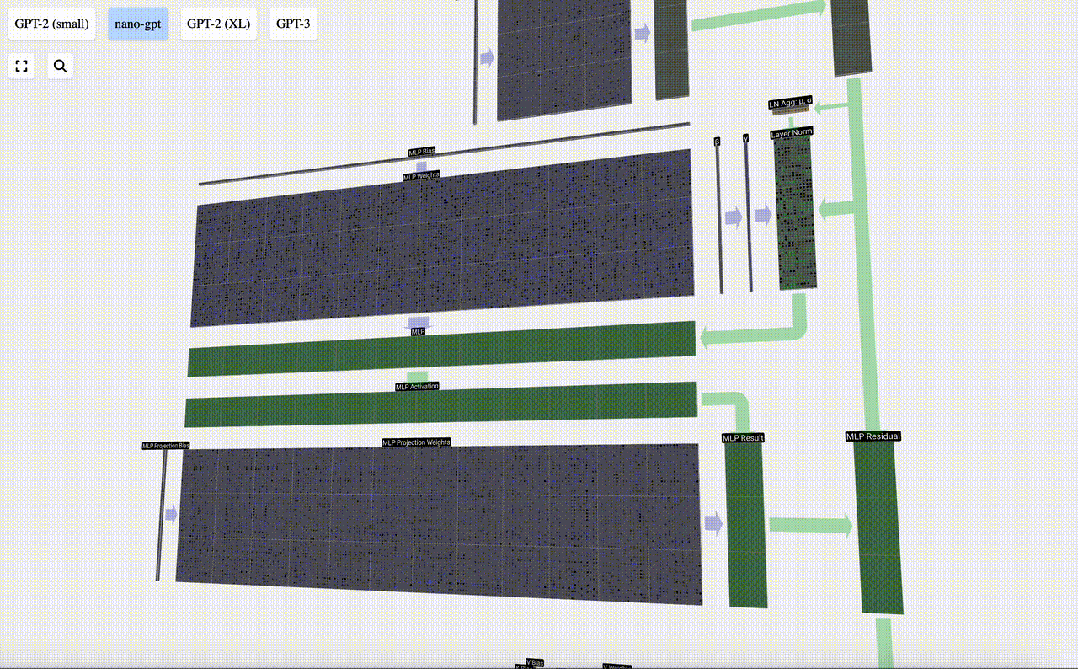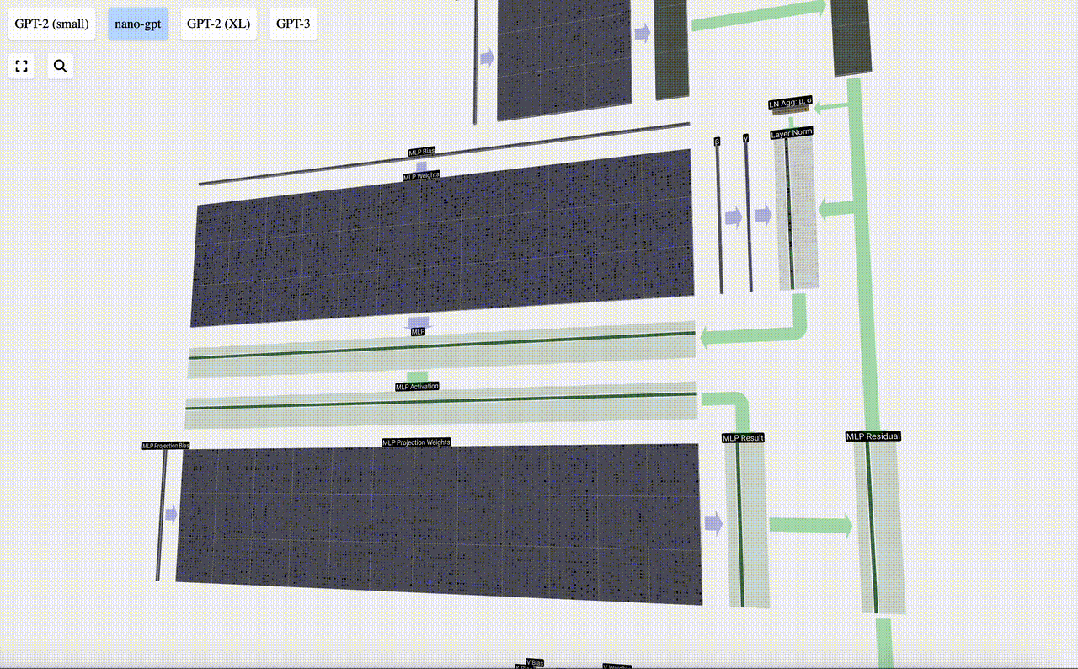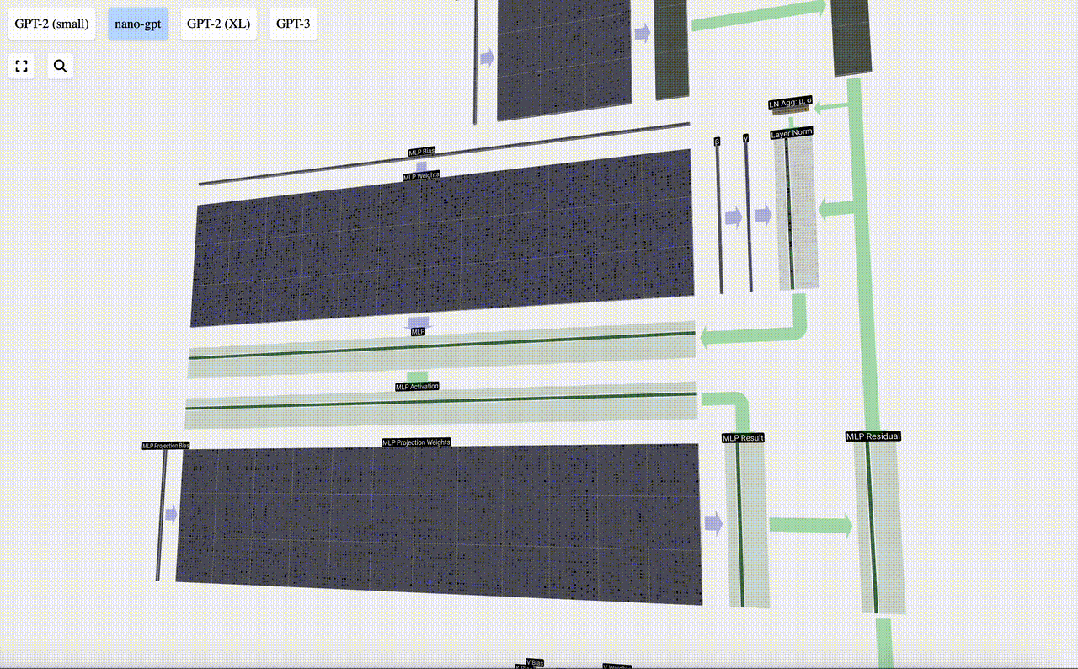 圖片
圖片
我們首先進行帶偏置的矩陣-向量乘法運算,將向量擴展為長度為4*C 的矩陣。(請注意,輸出矩陣在這里進行了轉置,這純粹是為了更加形象化)
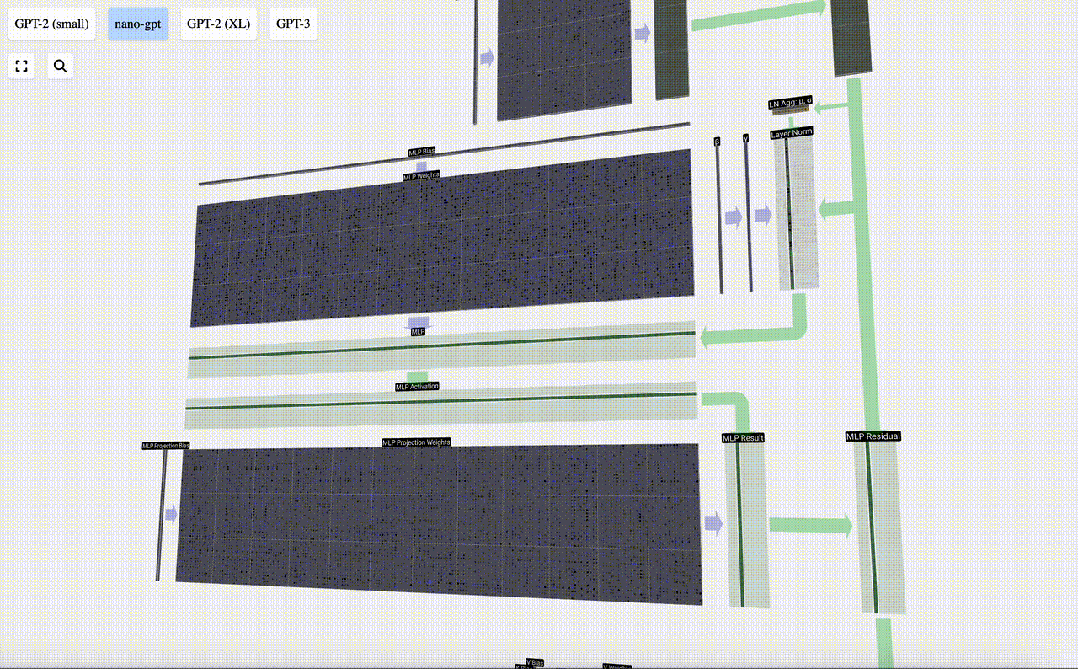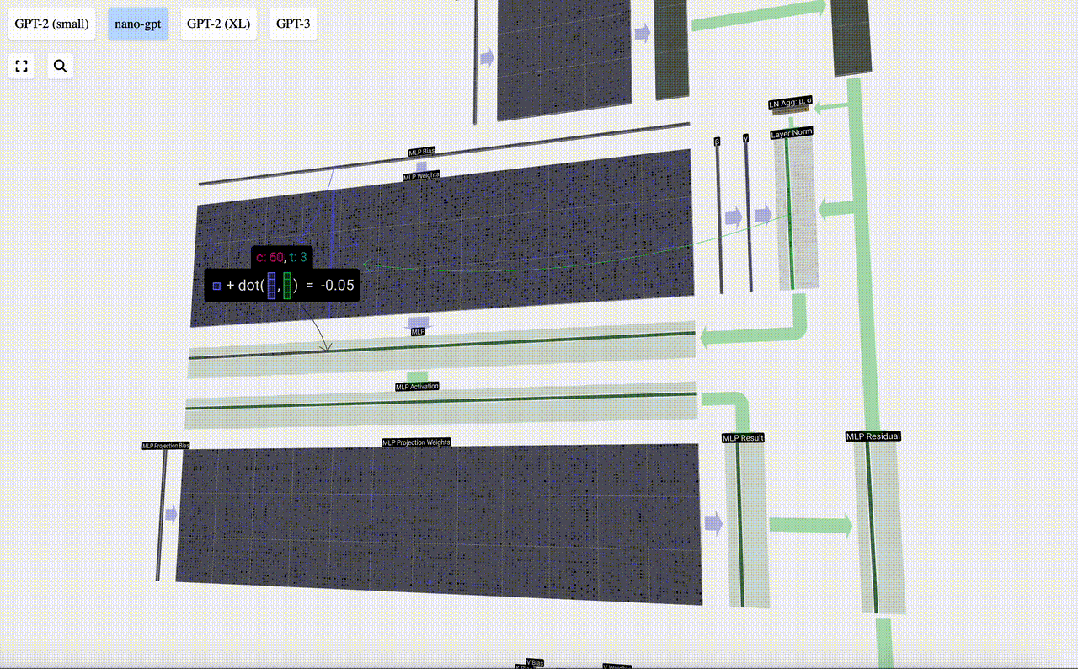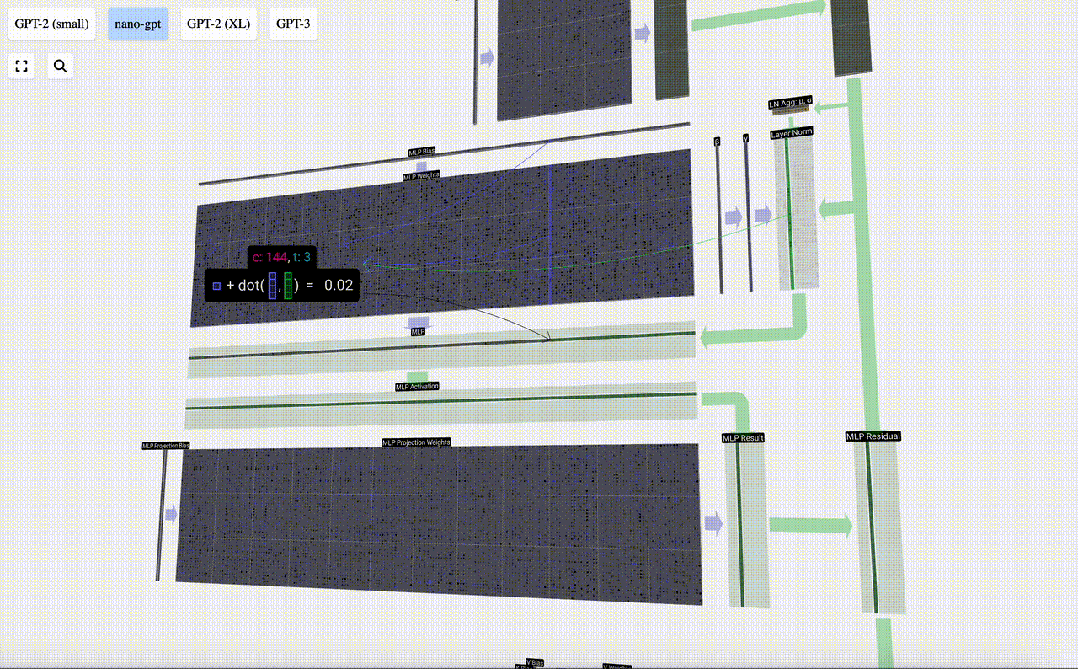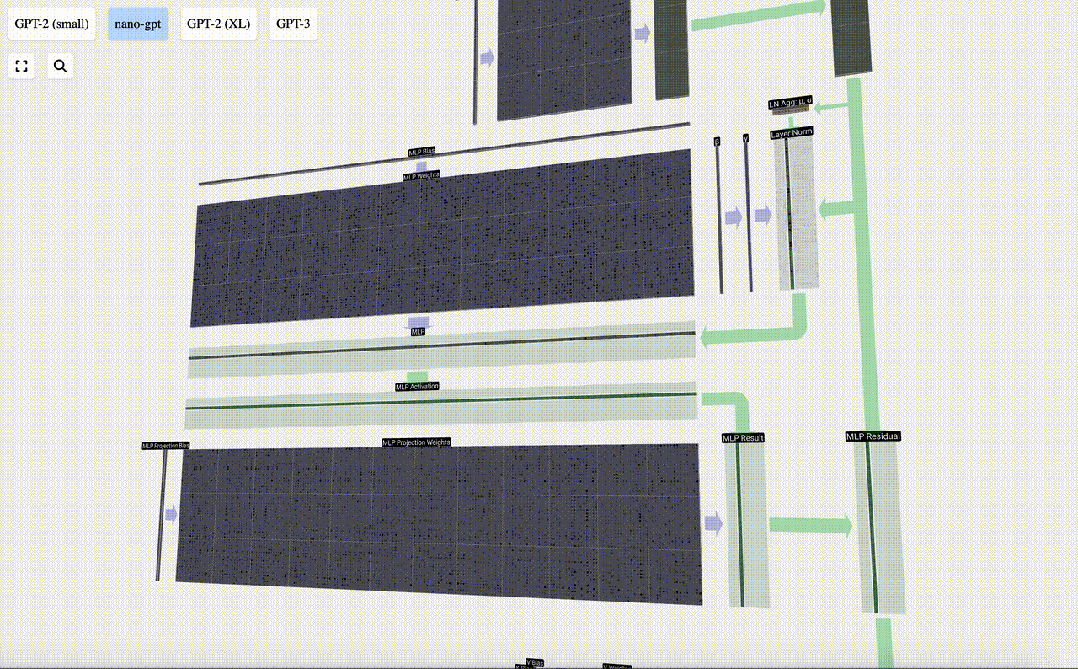 圖片
圖片
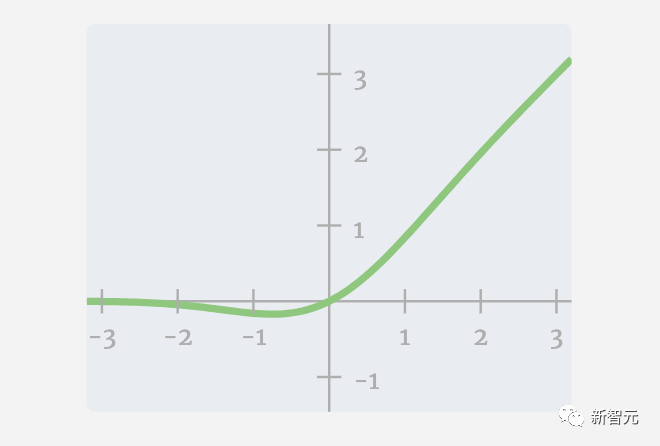
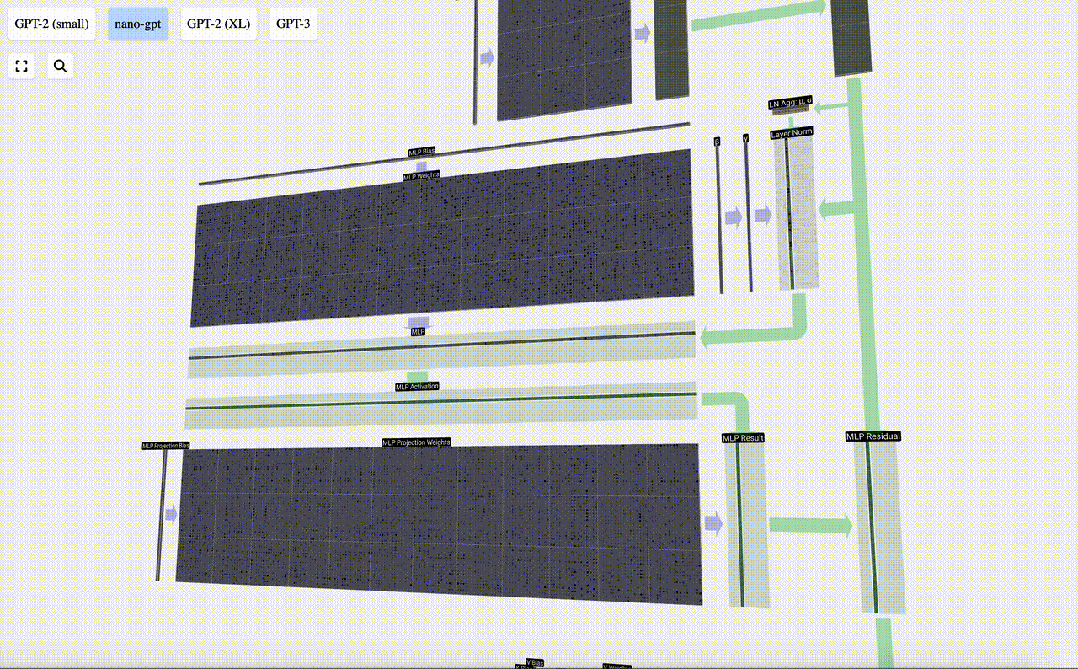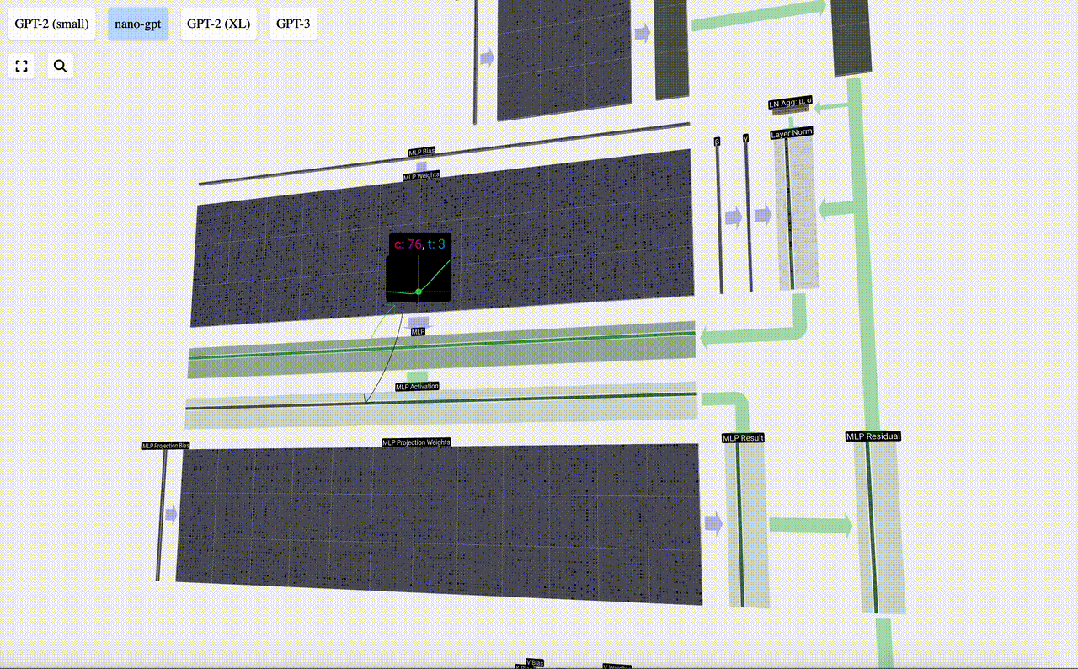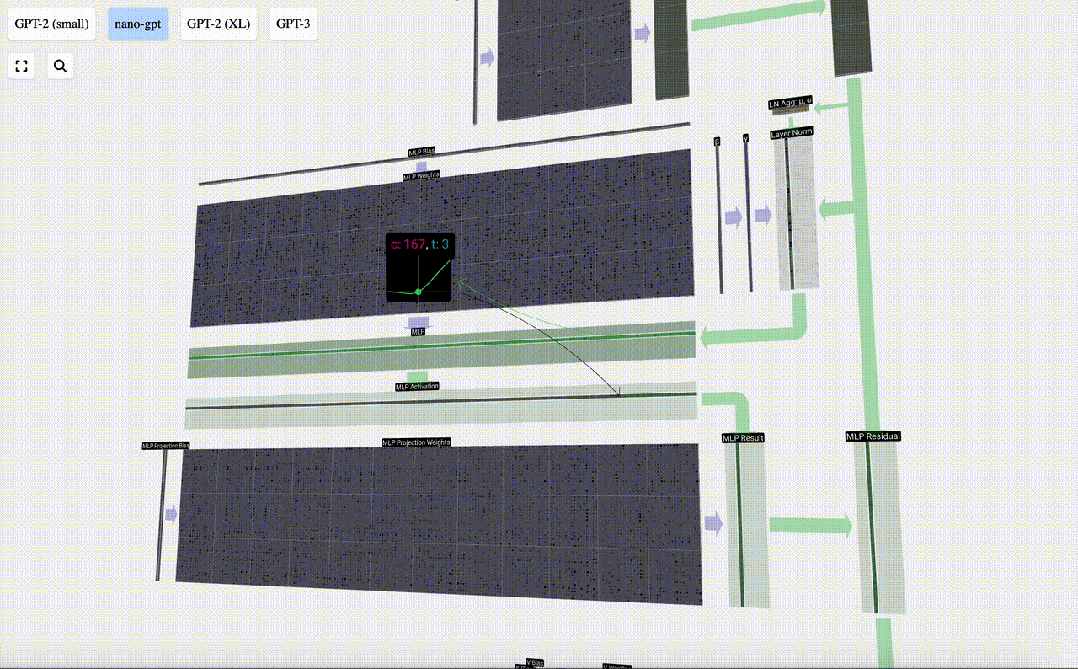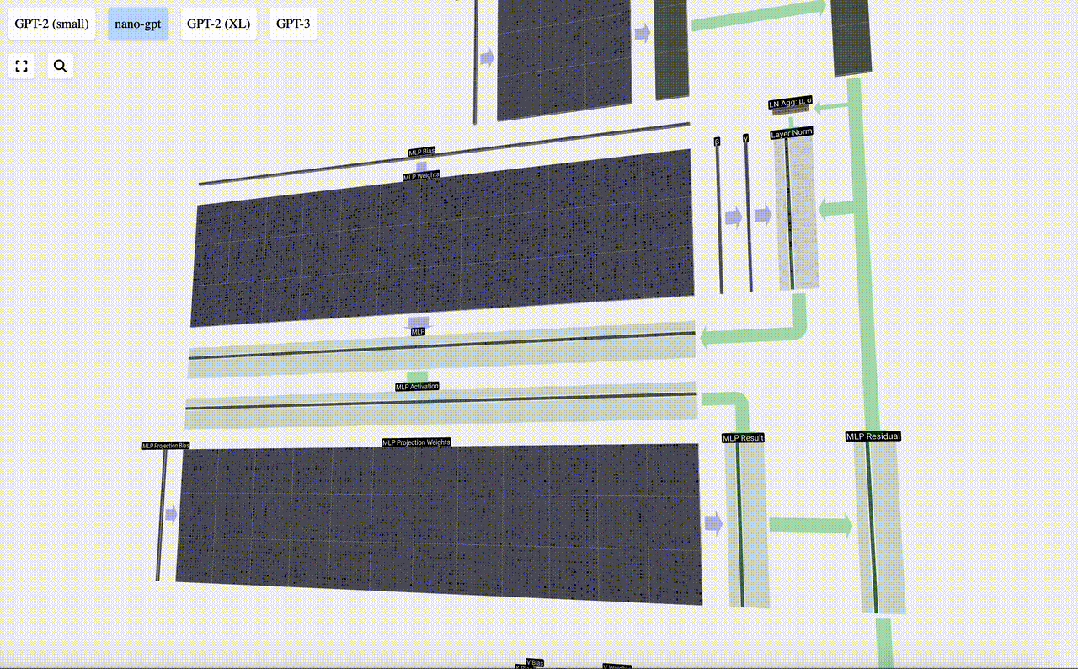
接下來,我們對向量的每個元素應用GELU激活函數。
這是任何神經網絡的關鍵部分,我們要在模型中引入一些非線性。使用的特定函數GELU看起來很像ReLU函數(計算公式為max(0,x)),但它有一條平滑的曲線,而不是一個尖角。
 圖片
圖片
 圖片
圖片
然后,我們通過另一個帶偏置的矩陣-向量乘法,將向量投影回長度C。
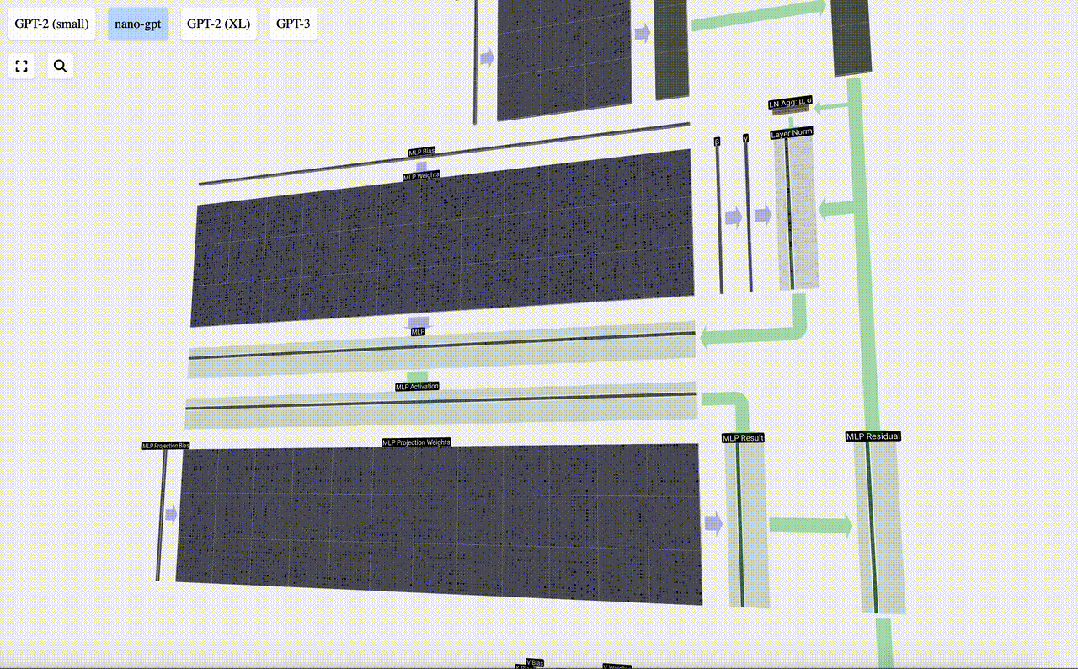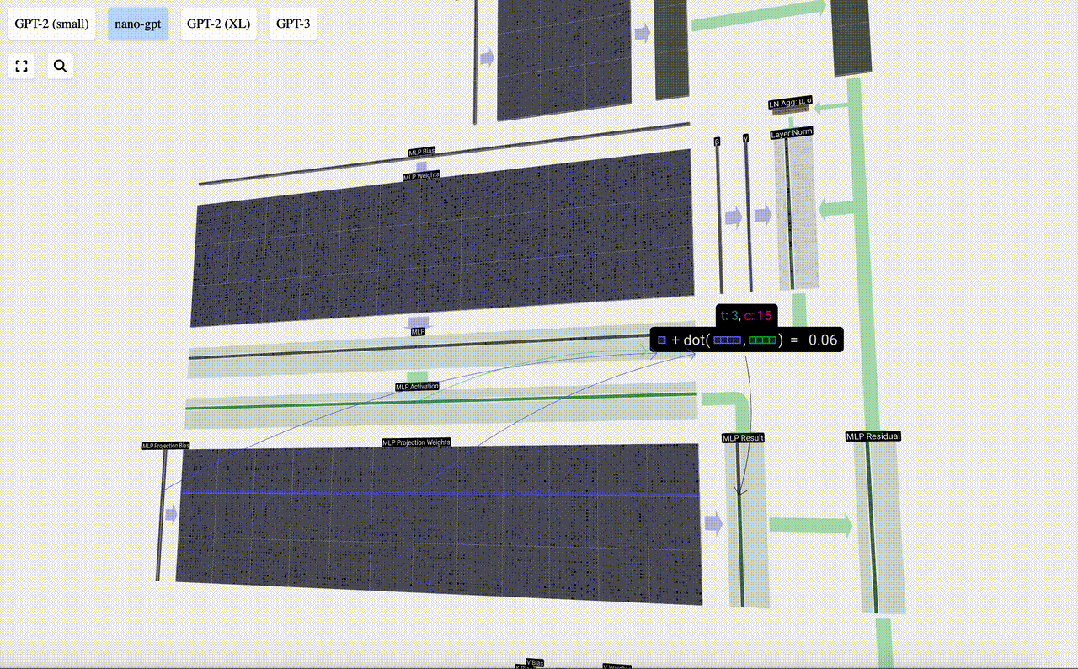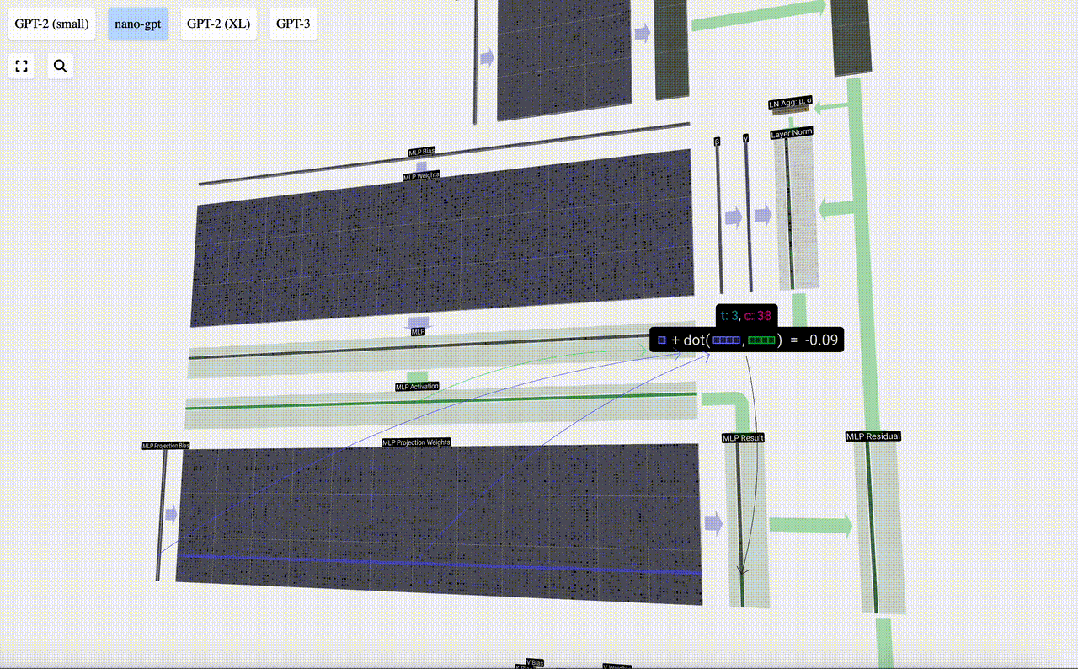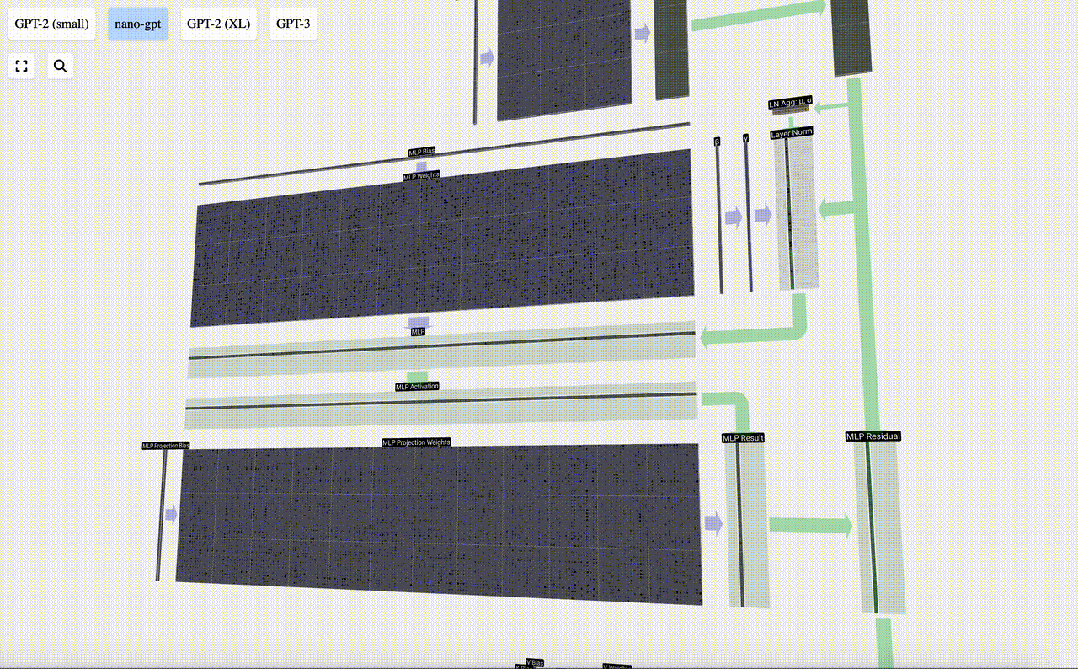 圖片
圖片
與自注意力+投影部分一樣,我們將MLP的結果按元素順序添加到輸入中。
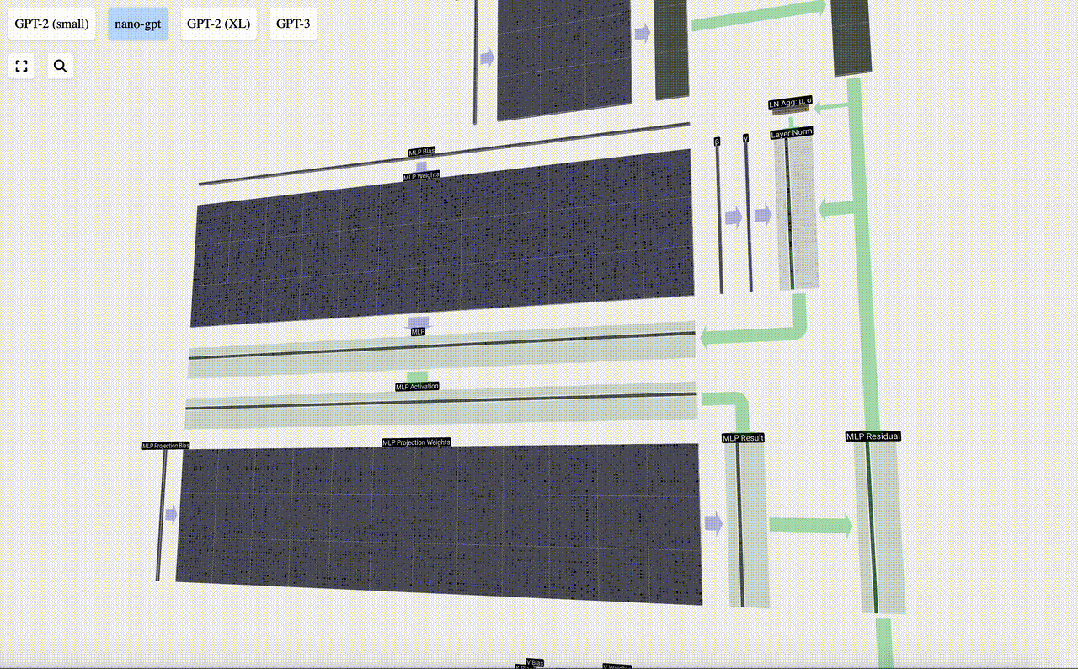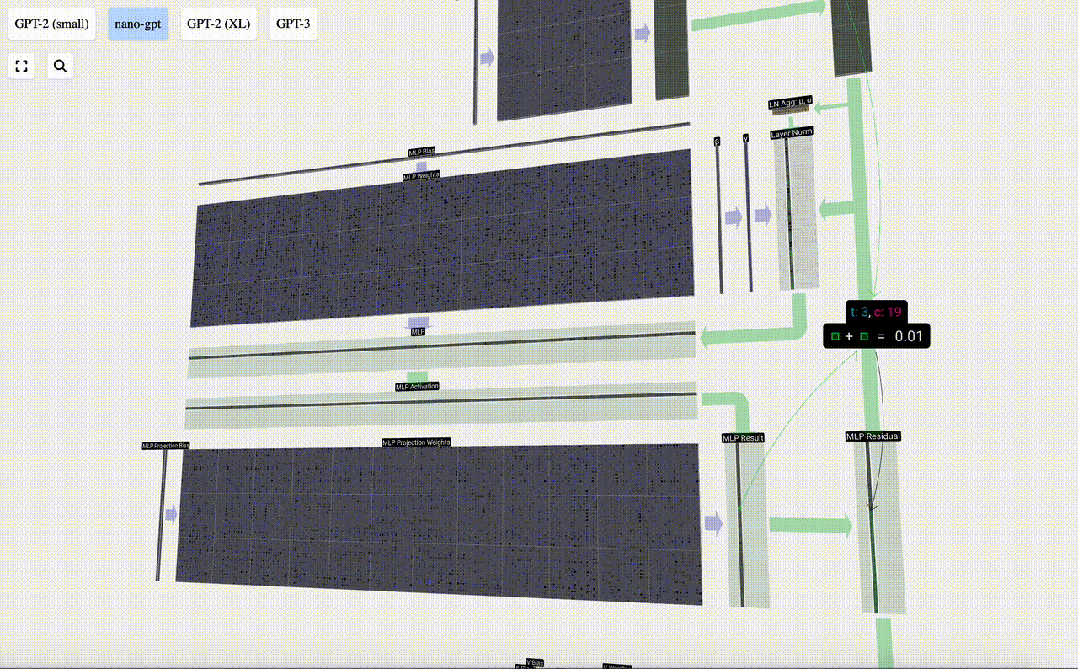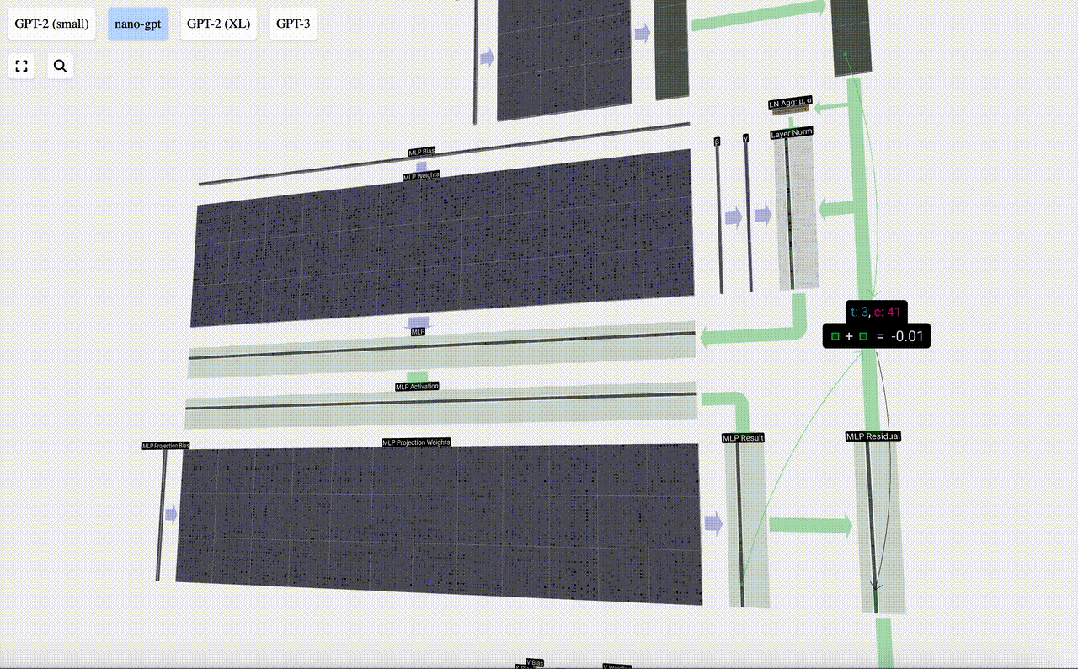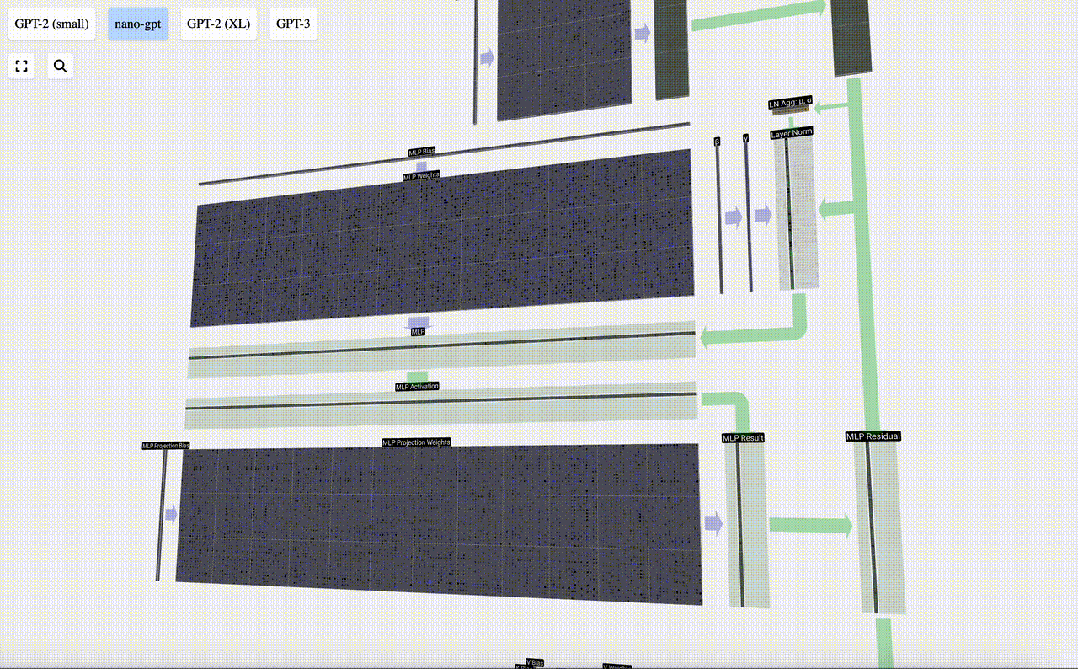 圖片
圖片
現在,我們可以對輸入內容中的所有列重復這一過程。
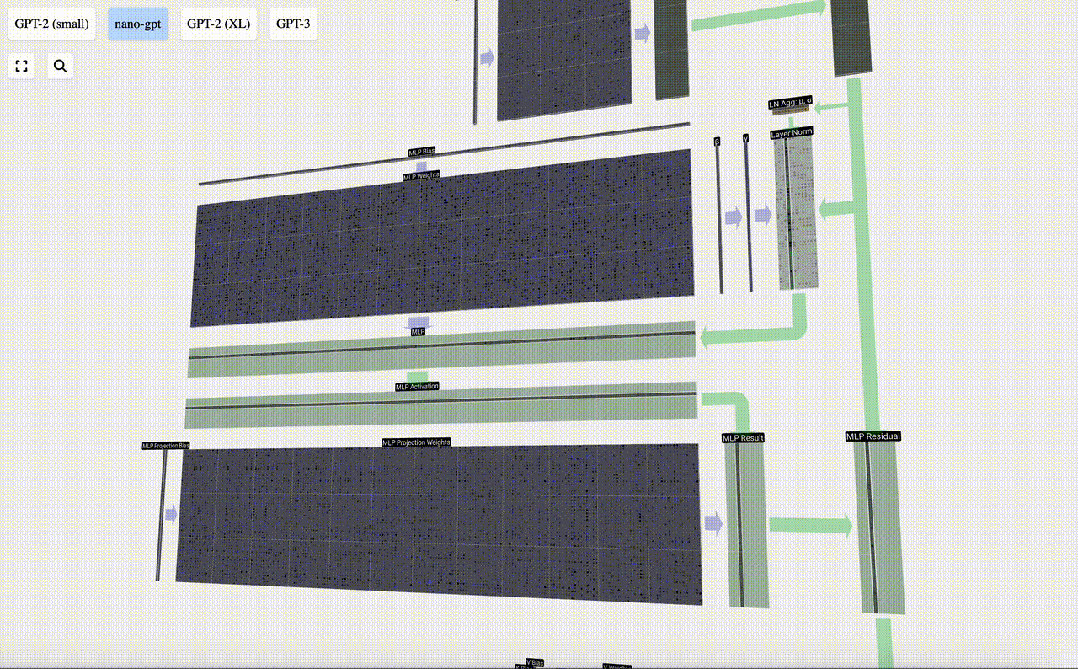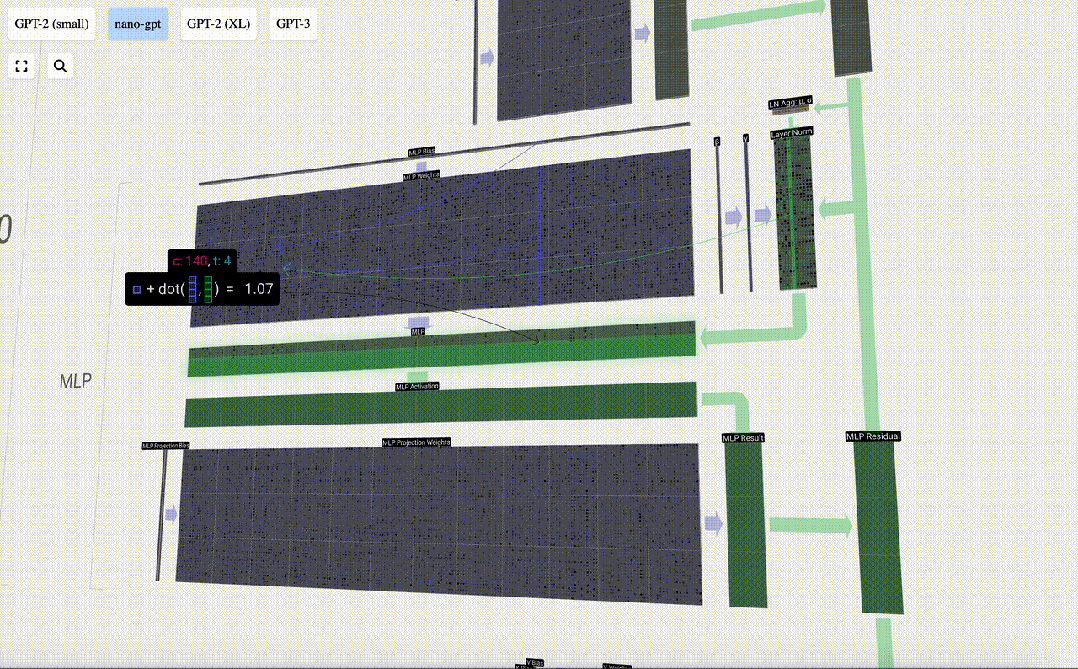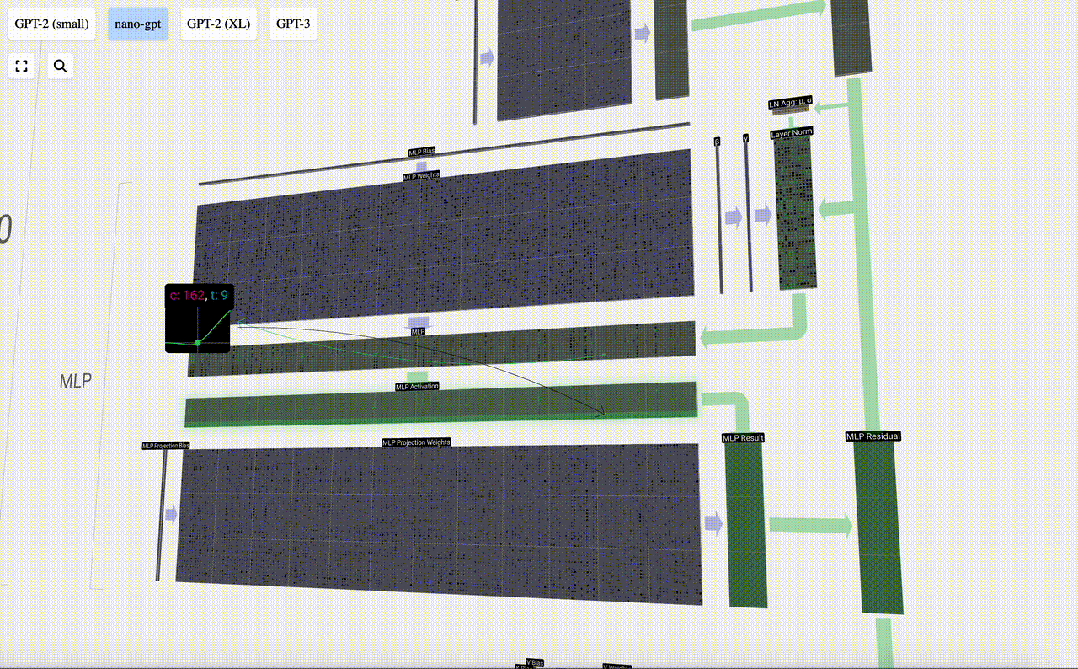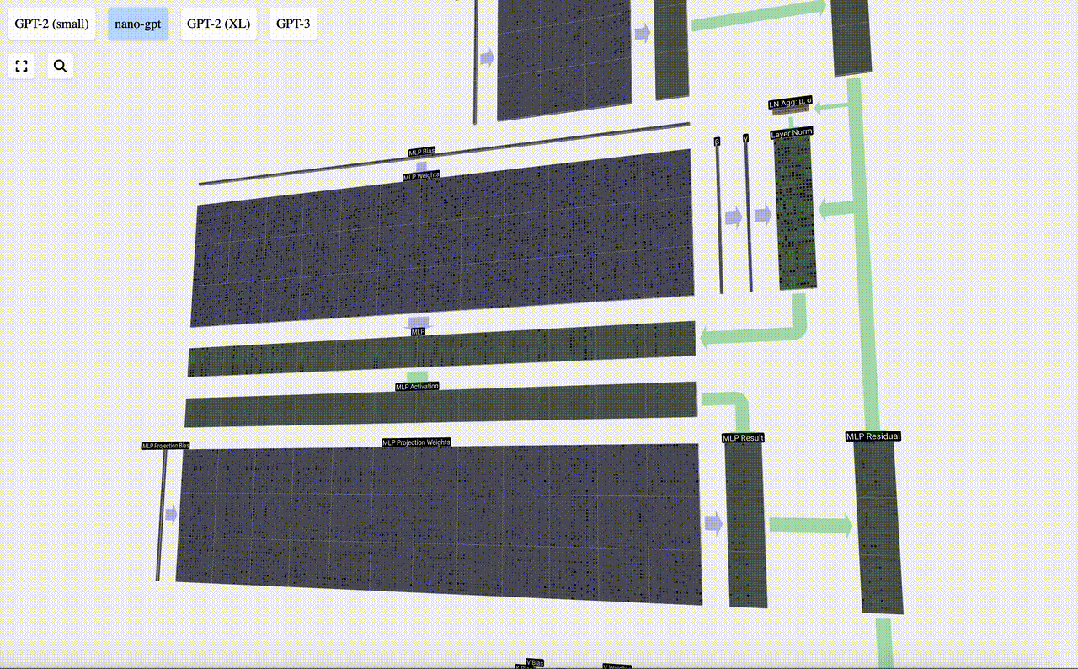 圖片
圖片
至此,MLP 完成。現在我們有了Transformer模塊的輸出,可以將其傳遞給下一個模塊了。
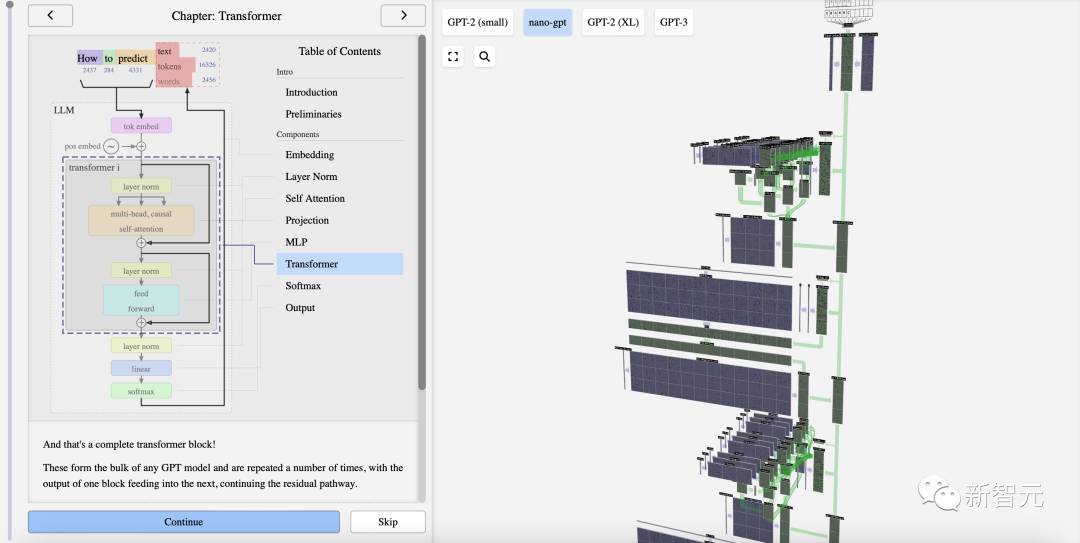
Transformer
這就是一個完整的Transformer模塊!
它們構成了任何GPT模型的主體,并且會重復多次,一個塊的輸出會輸入到下一個塊,繼續殘差路徑。
與深度學習中常見的情況一樣,很難說清楚這些層中的每一層在做什么,但我們有一些大致的想法:前面的層往往側重于學習較低層次的特征和模式,而后面的層則學習識別和理解較高層次的抽象概念和關系。
在自然語言處理中,底層可能學習語法、句法和簡單的詞匯關聯,而高層可能捕捉更復雜的語義關系、話語結構和上下文相關的含義。
 圖片
圖片
Softmax
softmax運算不僅是自注意力機制的一部分,如前文所述,它還會出現在模型的最后階段。
概括來說,softmax的目的是將向量中的值歸一化,使它們加起來等于1.0。但這并不是簡單地將各值除以總和那么簡單。相反,每個輸入值都會先被求指數。
a = exp(x_1)
這樣處理的效果是讓所有值變為正數。一旦得到了一個指數化的值向量,就可以將每個值除以所有值的總和,從而確保所有值的和為1.0。由于所有指數化的值都是正的,那么最終的值將介于0.0和1.0之間,也就是為原始值提供了一個概率分布。
softmax的過程就是這樣:簡單地對值進行指數化處理,然后除以它們的總和。
不過,這里有一個小麻煩。
如果輸入值很大,那么指數化后的值也會很大。這時,就將面臨一個大數除以另一個大的數的情況,進而導致浮點運算出現問題。
softmax運算有一個有用的特性:如果向所有輸入值添加一個常數,最終結果將保持不變。因此,可以在輸入向量中找到最大值,并從所有值中減去這個它,這樣可以確保最大值變為0.0,從而保持softmax運算的數值穩定。
在自注意力層,每個softmax運算的輸入向量是自注意力矩陣的一行(但只到對角線為止)。
與「層歸一化」類似,有一個中間步驟來存儲一些聚合值來提高處理效率。
對于每一行,需要記錄該行的最大值和經過移位與指數化處理后的值的總和。然后,為了得到相應的輸出行,可以執行一系列操作:減去最大值,進行指數化處理,再除以總和。
那么,為什么叫「softmax」呢?
這個運算的「hard」版本,稱為argmax,簡單地找到最大值,將其設為1.0,其他所有值設為0.0。相比之下,softmax運算是一種更「soft」的版本。
由于涉及指數運算,softmax運算會突出最大值,并將其推向1.0,同時還保持了對所有輸入值的概率分布。這樣的處理方式不僅能捕獲到最可能的選項,還能捕獲到其他選擇的相對可能性,實現了更細微的表示。
 圖片
圖片
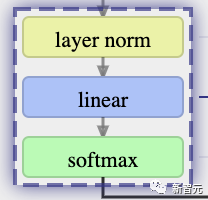
輸出
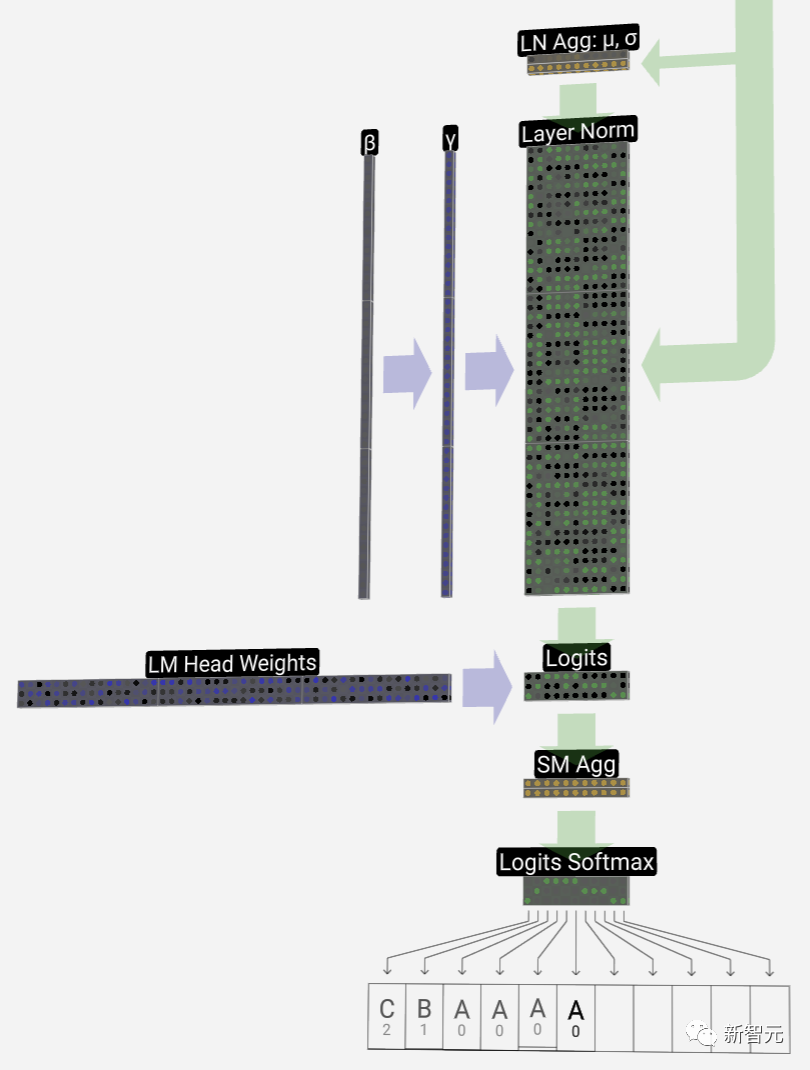
最后一個Transformer塊的輸出,首先會經過層歸一化,然后再進行線性變換(矩陣乘法),不過這次沒有加入偏置項。
 圖片
圖片
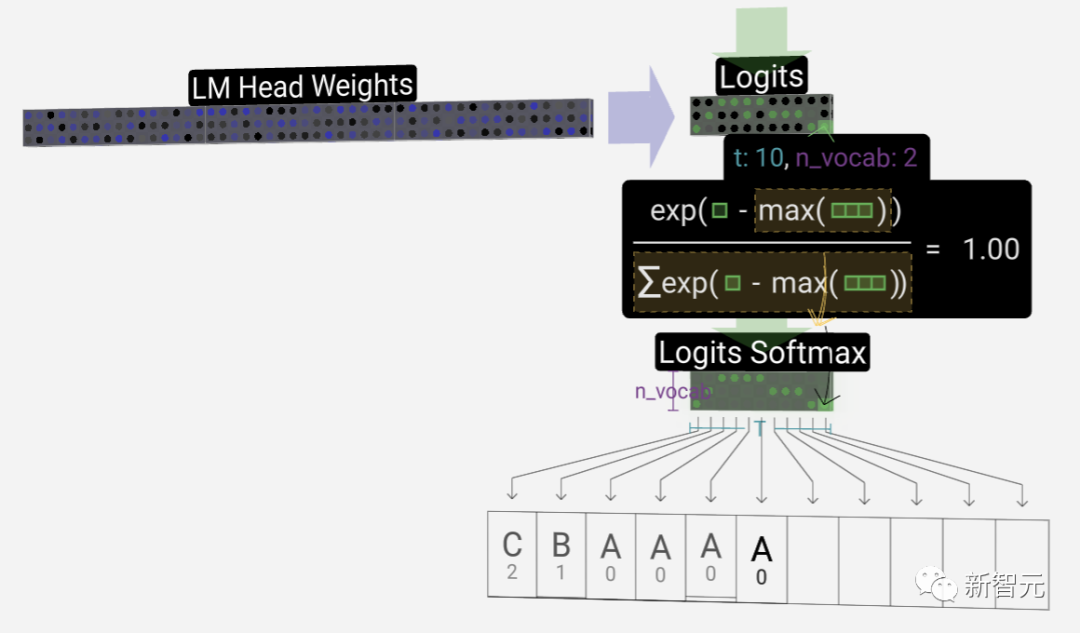
最后的transformation會將每個列向量的長度從C變為nvocab。因此,實際上是在為每一列的詞匯庫中的每個詞產生一個得分——logits。
「logits」這個術語源自「log-odds」,也就是每個token的對數幾率。之所以會使用「Log」(對數),是因為接下來應用的softmax會進行指數轉換,從而把這些得分變成「幾率」或者說概率。
為了把這些得分轉化為更加直觀的概率值,需要先通過softmax來進行處理。現在,每一列都得到了模型對詞匯表中每個詞所分配的概率。
在這個特定的模型中,它已經有效地學會了所有關于如何排序三個字母的問題的答案,因此給出的概率值,也很大概率會傾向于正確答案。
在對模型進行時間步進時,需要利用最后一列的概率值來決定下一個要添加到序列中的token。舉個例子,如果已經向模型輸入了6個token,那么就會用第6列的輸出概率來決策。
這一列輸出的是一系列概率值,因此必須從中選擇一個作為序列的下一個元素。這需要通過「從分布中采樣」來實現。也就是說,會根據概率值的權重隨機選擇一個token。例如,一個概率為0.9的token有90%的概率被選中。
當然,還有其他選擇方法,比如始終選擇概率最高的token。
此外,還可以通過使用溫度參數來控制分布的「平滑度」。較高的溫度會讓分布更均勻,而較低的溫度則會讓分布更集中于概率最高的token。
在應用softmax之前,先用溫度除以logits(線性變換的輸出)。由于softmax中的指數化對較大的數值影響較大,因此將所有數字拉近會減少這種影響。
 圖片
圖片
網友驚掉下巴
有網友表示,看到算法復雜度能夠在三維空間中,以如此清晰的方式呈現出來,讓我驚掉了下巴!

 圖片
圖片
與NanoGPT相比,GPT-3簡直是一個怪物。
 圖片
圖片
這看起來比我們在 2005 年在大學里看到的簡單神經網絡要復雜1000倍。我正在考慮未來5-10年,通用人工智能 (AGI)將要走向哪里?
 圖片
圖片
參考資料:








































