在CV、ML等領域經常用到的神經場網格模型，如今有了理論框架描述其訓練動力學和泛化性能。

來自上交大，港中文和酷哇科技的研究人員，對用來表示神經場的網格模型進行了詳盡的理論分析，還提出了新的模型。

該項目不僅在盲審階段獲得了三位審稿人一致的滿分意見（5/5/5）, 還獲得了CVPR24最佳論文提名。

作者指出，利用網格模型來表示神經場是一種常見的技術，但對這些模型的系統分析仍然缺失，阻礙了這些模型的改進。

對此，作者基于正切核理論（GTK）提出了新的框架，促進了對各種基于網格模型的一致和系統的分析。

此外，該框架還激發了一個名為乘法傅里葉自適應網格（MulFAGrid）的新型模型，具有強大的泛化性能。

本工作也即將在Jittor深度學習框架平臺進行實現和開源，接下來就來一起了解下。

提出網格模型新理論框架

首先了解一下什么是神經場。

神經場是基于坐標的網絡，表示一個場，實質上是一種連續參數化，代表一個物體或場景的物理量。

神經場在計算機視覺和其他研究領域的各種任務中顯示出了顯著的成功，其典型應用如下圖所示：

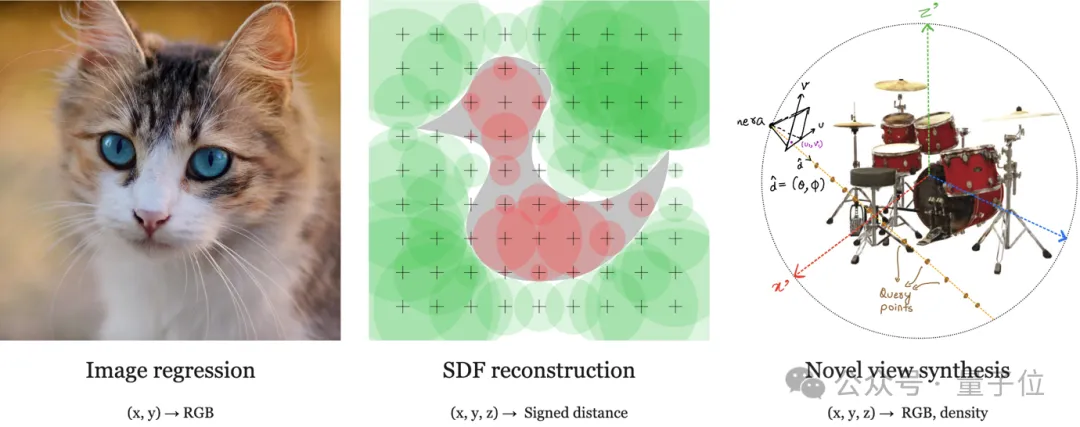
神經場有多種不同的模型類型，作者的研究主要針對其中的網格模型（grid-based models）展開。

網格模型在參數化和功能上與傳統的神經網絡（如MLP）有根本不同，主要包括：

• MLP往往包含多層非線性神經網絡；
• MLP沒有顯式查詢的過程；
• MLP的輸入不一定是位置坐標。

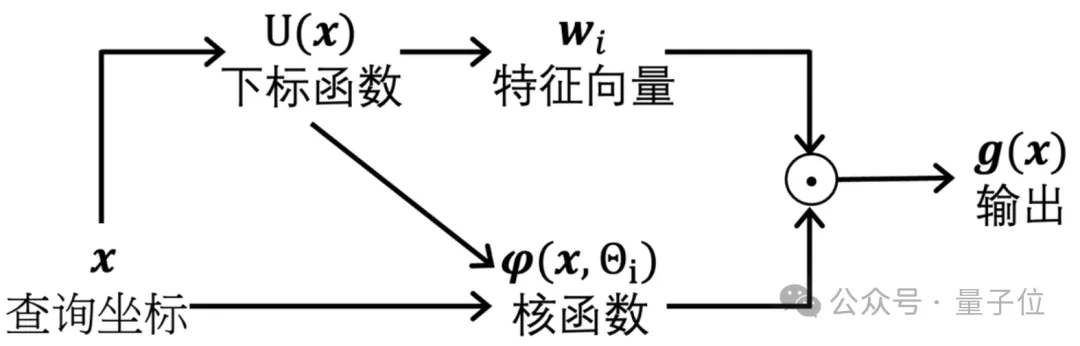
而網格模型以查詢坐標為輸入，該坐標被發送到下標函數以從網格中獲取一組特征向量。

然后，模型輸出核函數和這些特征向量的加權平均值，該模型需要學習參數的主要是特征向量。

最簡單的核函數是不含參數的插值算法（如最近鄰算法或者雙線性插值算法），核函數里面也可以包含可學習的參數。

為了更好地理解和增強網格模型，作者通過三個主要問題進行了研究：

• 如何理解網格模型的訓練動態？
• 如何衡量網格模型的泛化性能？
• 如何設計一個更好的網格模型？

為了解決這些問題，研究團隊提出了一個基于正切核（Tangent Kernels）的理論框架。

正切核這一概念來自于著名的深度學習理論文章神經正切核（Neural Tangent Kernels，NTK）。

NTK 是一種核函數，最初由研究者在研究神經網絡的訓練過程時提出的。

當神經網絡在參數空間中靠近其初始值時，通過對神經網絡梯度下降優化過程的分析，發現網絡的行為可以用一個固定的核函數來描述，這個核函數就是神經正切核。比如神經網絡的輸出可以用其參數的梯度來表示。

在訓練過程中，網絡參數的更新會導致輸出的變化，而這種變化在參數空間中的變化速率可以用梯度來表示。NTK 定義了兩個輸入數據點的輸出變化之間的相似度。

形式上，對于輸入數據點xi和xj，神經正切核Θ(xi，xj)可以定義為網絡輸出對參數的梯度的內積：

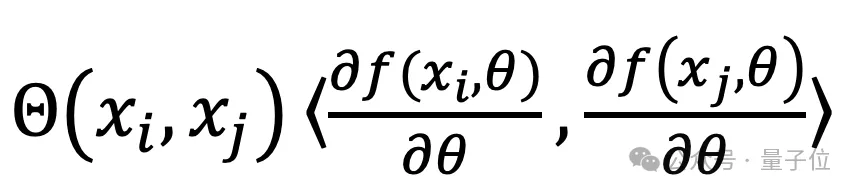
其中，f(x,θ)是神經網絡的輸出，θ是網絡的參數。

理論結果表明，網格模型的近似和泛化性能與網格切線核（GTK）有關。

GTK被定義為一個正半定矩陣，它測量梯度空間中兩個數據點之間的距離。

下面的式子展示了GTK的定義：g是由w(t)參數化的網格模型，X是一個數據集，其中Xi是第i個數據。GTK可以這樣表示：

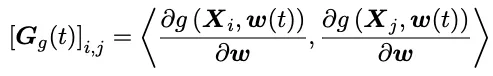
注意這個形式跟神經正切核（NTK）的形式是吻合的，因為他們都是正切核，他們的主要區別是適用的模型不同，GTK主要適用于網格模型。

后面可以看出，因為網格模型本質上比較簡單純粹，所以GTK的理論基本不需要近似，但是NTK的理論需要網絡無窮寬的假設才能成立。

研究團隊得到的的定理一（網格模型優化定理）說明，網格模型的模型參數根據微分方程（如下面方程所示）演化。

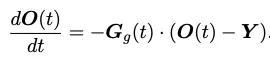
這里O(t)表示網格模型的輸出，G(t)表示網格模型的GTK，而這里的Y表示數據集的標簽（向量化，Yi表示第i個數據的標簽）。

這里簡單對這個定理進行一個證明，模型的參數在梯度下降算法下按照下面的公式進行迭代：

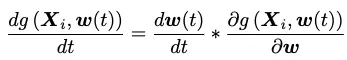
此時考慮一個L2損失函數L，它的梯度將被運用于更新模型參數，因此我有：

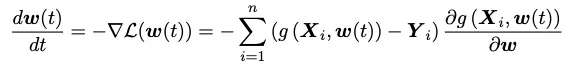
結合上面兩個方程，可以得到：

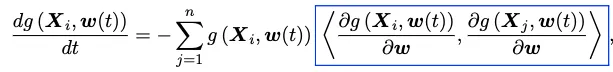
這里藍色方框里就是我們關心的GTK。這個定理有什么意義呢？

直觀地講，有了這個定理我們就可以預測模型的效果，也就是說不用親自“煉丹”就能確定模型的好壞。

下面這張圖小結了定理一的內容。

接下來，研究團隊又提出了另一個定理——GTK不變定理。

定理2指出，網格模型的GTK在訓練期間保持不變。這意味著無論網格模型的大小如何，初始GTK在整個訓練過程中保持恒定。

這一定理揭示了GTK是由模型和數據集決定的一個內在特性，與模型的訓練過程無關，有了這個定理，自然也不難理解網格模型的很多性質都與GTK有關了。

定理三則可以描述網格模型的泛化性能。

在理論深度學習中，泛化性能的好壞通常由泛化界（generalization bound）來刻畫。

該定理揭示了網格模型的泛化界由一個特定的度量Δ決定，而Δ = Y^T·G^(-1)·Y，與網格模型的GTK和數據集的標簽有關。

形式化的說，該泛化界提供了模型性能的概率保證。該定理說明了模型的泛化性能既與GTK有關，也與數據集的結構有關。結合該定理與GTK的特征值，可以獲得更多關于泛化性能的信息。

基于GTK的全新網格模型及實驗結果

GTK理論可以為具有更好訓練和泛化性能的網格模型的設計賦能，研究團隊也基于該理論審計了一種新的網格模型，名為MulFAGrid。

該模型使用傅里葉特征來提升高頻信號的學習，并采用乘法濾波器來為模型提供節點信息，示意圖如下：

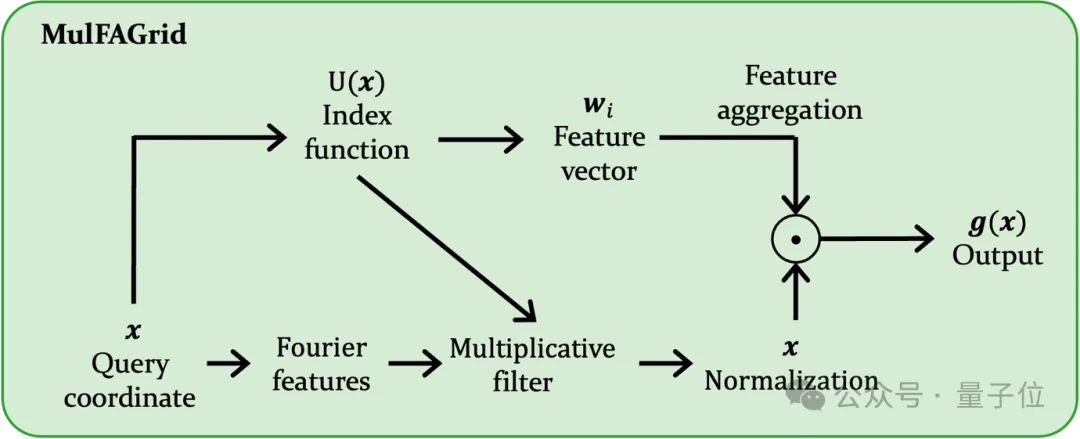
然后，作者基于GTK理論對MulFAGrid進行了一組數值實驗。

首先，在頻譜分析中，MulFAGrid顯示了比較寬的頻譜，特別是在高頻域。這一特性導致高頻成分的收斂速度更快。

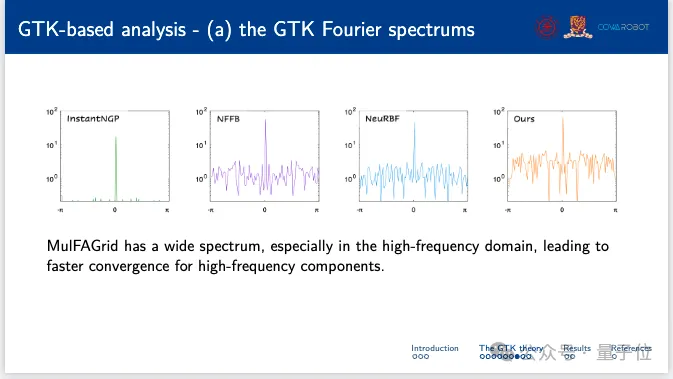
在這個實驗中，作者構建了一個包含兩個數據點及其對應標簽的數據集。MulFAGrid對于大多數標簽值表現出更緊的泛化界，表明其泛化性能更好。

精確度方面，相對于各種基線方法和作者的誤差圖，MulFAGrid都提供了更準確的擬合，展示了其優越的性能。

下面的誤差圖衡量了預測圖像與真實圖像的差異。

另外，模型在擬合二維圖像和三維符號距離函數（SDF）的性能測試中，MulFAGrid也顯現出了較高的準確性和效率。

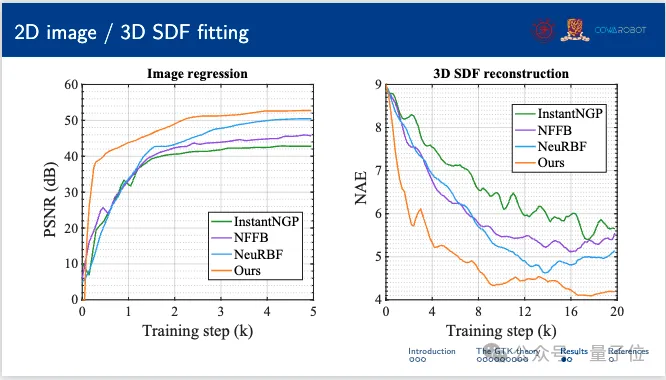
最后，作者探究了MulFAGrid在新視角合成方面的能力。詳細結果表明，MulFAGrid在生成高質量的新視角方面表現出色，突顯了其實際應用性。

作者簡介

本文第一作者趙澤林，在上海交通大學計算機系獲得學士學位，即將進入佐治亞理工學院攻讀博士學位。

趙澤林曾在NeuRIPS，ECCV，CVPR，AAAI等頂會發表四篇一作論文，引用數超過600。

他所在的ReThinklab實驗室由上海交通大學人工智能學院與計算機系嚴駿馳教授創立，主要研究方向是機器學習及交叉應用。

嚴駿馳教授帶領實驗室發表第一/通訊作者CCF-A類論文超百篇，谷歌引用過萬次，獲PaperDigest評選的最具影響力AAAI21、IJCAI23論文榜首。

嚴駿馳教授長期任機器學習三大會議ICML/NeurIPS/ICLR領域主席，模式識別旗艦期刊TPAMI、PRJ編委。實驗室學生獲得挑戰杯特等獎、CCF優博/CV新銳獎、交大學術之星等榮譽和本科生自然科學基金。

本文通訊作者來自香港中文大學數學系研究助理教授范鳳磊博士，他所在的Center for Mathematical AI由曾鐵勇教授創立。中心自2018年成立以來，在中心主任曾鐵勇教授的帶領下，先后承擔科技部國家重點研發計劃項目等一系列關鍵項目。

范鳳磊博士于美國倫斯勒理工學院（Rensselaer Polytechnic Institute）獲得博士學位，導師為國際知名影像專家王革教授，主要研究方向是腦啟發智能以及神經網絡的數學理論，在JMLR，TMI，TNNLS，TCI等雜志發表論文二十余篇，引用數過千。曾獲得IBM AI Horizon Scholarship和國際神經網絡協會（INNS）2021年杰出博士論文獎。

論文地址：https://arxiv.org/abs/2403.20002
項目主頁：https://sites.google.com/view/cvpr24-2034-submission/home