生成式模型（GMs）的設(shè)計宗旨是模仿人類的各種行為，例如回答問題、創(chuàng)作藝術(shù)、唱歌等，人類在這些領(lǐng)域都展現(xiàn)出高超的技能。

然而，模型在訓(xùn)練過程中實際上只專注于一個核心目標(biāo)，即最小化模型輸出的交叉熵損失，確保模型的輸出分布盡可能地接近人類標(biāo)注的分布。

換句話說，模型的能力上限可能已經(jīng)被定死了，最多只能達到人類專家在其專業(yè)領(lǐng)域的表現(xiàn)水平。

但最近來自哈佛大學(xué)、加州大學(xué)圣巴巴拉分校（UCSB）、普林斯頓大學(xué)的研究結(jié)果表明，模型在某些特定的領(lǐng)域可以實現(xiàn)「超越（transcend）訓(xùn)練數(shù)據(jù)中的專家水平」的性能，青出于藍而勝于藍。

論文鏈接：https://arxiv.org/pdf/2406.11741

研究人員選擇國際象棋作為研究目標(biāo)展現(xiàn)模型的超越性（transcendence），因為其規(guī)則和玩法是清晰且有限的。

然后使用Transformer模型基于公開的人類國際象棋對局數(shù)據(jù)集進行訓(xùn)練，使其能夠預(yù)測對局中的下一步走法。

為了探索模型是否能夠超越人類專家，研究人員特意選擇了一個沒那么強的數(shù)據(jù)集，其中包含的人類玩家等級（使用Glicko-2對棋手等級進行評分）都不超過某個特定的分數(shù)。

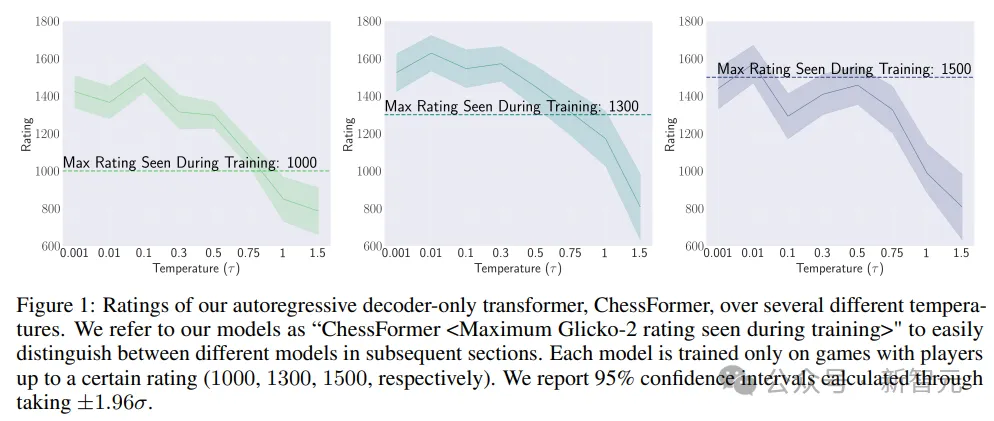
實驗結(jié)果顯示，模型不僅可以達到該分數(shù)，甚至部分模型還能實現(xiàn)性能超越，表明模型在某些情況下能夠超越提供訓(xùn)練數(shù)據(jù)的人類專家。

該研究主要包括以下幾個方面：

1. 在生成模型中形式化了超越（transcendence）的概念；

2. 通過將去噪專家的情況與模型集成聯(lián)系起來，找到了解釋超越的一個關(guān)鍵原因；

3. 在特定技能水平的玩家數(shù)據(jù)集上訓(xùn)練國際象棋Transformer，并證實了模型在低溫設(shè)置下能夠超越其訓(xùn)練數(shù)據(jù)中專家的最高等級。

4. 通過降低采樣溫度，對獎勵變化的分布進行可視化，并發(fā)現(xiàn)性能的提升主要歸因于在相對較小的一部分狀態(tài)下的大幅改進。

5. 探索了數(shù)據(jù)集多樣性的必要性，以及在數(shù)據(jù)集不夠多樣化時模型無法實現(xiàn)超越的情況。

超越性的定義

研究人員首先描述了一個理論框架，用于構(gòu)建和評估能夠基于輸入數(shù)據(jù)預(yù)測輸出的機器學(xué)習(xí)模型：

1. 輸入空間X和輸出空間Y，其中X可以是任何長度，而Y是有限的。

2. 函數(shù)類F是所有將輸入X映射到Y(jié)上概率分布的函數(shù)的集合，其中每個函數(shù)f ∈ F定義了給定輸入x時輸出y的條件概率。

3. 存在一個輸入分布p，其對X中的所有輸入都有非零概率。

4. 數(shù)據(jù)由k位專家進行標(biāo)注，每位專家提供一個函數(shù)fi，定義了給定輸入x時輸出y的概率分布。所有專家的分布被混合起來形成了一個混合分布。

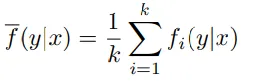
5、由專家標(biāo)注的過程生成的X和Y上的聯(lián)合概率分布D。

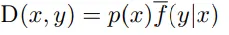
6、獎勵函數(shù)r，為每個輸入-輸出對分配一個獎勵值

7、選擇一個測試分布ptest，并定義了在ptest上的平均獎勵Rptest(f)，即對所有可能輸出的獎勵的期望值。

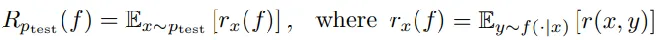
8、模型的目標(biāo)是找到在聯(lián)合分布D上的交叉熵損失最小的函數(shù)，其中交叉熵損失是衡量預(yù)測概率分布與真實概率分布差異的指標(biāo)。

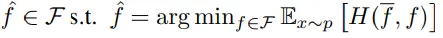
9、優(yōu)化過程：學(xué)習(xí)者通過最小化交叉熵損失來選擇最優(yōu)的預(yù)測函數(shù)，包括對F中的所有可能函數(shù)進行評估和選擇。

基于上述框架，超越性（transcendence）可以被定義為，在特定的函數(shù)設(shè)置和概率分布下，學(xué)習(xí)到的預(yù)測器在測試分布ptest上的平均獎勵超過了所有專家（fi）中的最高獎勵值。

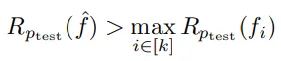
但這里討論的是一個理想化的情況，學(xué)習(xí)器可以訪問無限的數(shù)據(jù)，并且可以選擇任何函數(shù)來擬合數(shù)據(jù)，不受架構(gòu)或優(yōu)化方法的限制。

不過，即使在這種理想化的條件下，如果沒有對數(shù)據(jù)分布進行適當(dāng)?shù)男薷模揭部赡苁菬o法實現(xiàn)的。

在介紹這個理論框架時，研究人員做出了一些簡化的假設(shè)，比如所有專家使用相同的輸入分布，所有輸入在訓(xùn)練分布下都有非零概率，專家是隨機均勻選擇的等等。

超越的條件

低溫采樣對于實現(xiàn)超越（transcendence）是必要的

在生成模型中，采樣溫度是一個控制生成過程隨機性的參數(shù)。低溫采樣意味著模型在生成預(yù)測時更加確定，傾向于選擇概率最高的輸出，從而減少噪聲和隨機性，提高預(yù)測的準(zhǔn)確性。

定理一：無論選擇哪些專家函數(shù)和測試分布，總存在至少一個專家預(yù)測器，在測試分布上的獎勵大于等于學(xué)習(xí)到的預(yù)測器。

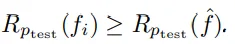
當(dāng)前的理論框架假設(shè)所有專家對于給定的輸入x被均勻采樣，即每個專家對輸入x的預(yù)測被賦予相同的重要性。

未來也可以考慮使用貝葉斯加權(quán)，可以更有效地結(jié)合專家的意見，可能會提高預(yù)測器的性能。

使用低溫度采樣實現(xiàn)超越性

定理2：如果存在某個溫度值??在0到1之間，使得在這個溫度值下或更低的溫度下，通過溫度采樣得到的預(yù)測器的性能（即在測試分布上的獎勵）高于所有專家，那么argmax預(yù)測器的性能也會高于所有專家。

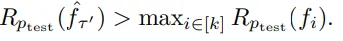
低溫采樣可以被看作是在專家之間進行「多數(shù)投票」的過程，如果專家們對于最佳動作有顯著的預(yù)測概率，那么通過多數(shù)投票得出的結(jié)果可能就會選擇最佳動作。

當(dāng)多個專家對最佳動作有共識時，這種共識可以通過多數(shù)投票被識別出來，從而提高整體的預(yù)測性能，體現(xiàn)了「群體的智慧」，即集體決策可能優(yōu)于個體決策的現(xiàn)象。

通過這種方式，模型不僅復(fù)制了專家的知識，而且通過集體智慧提高了性能，實現(xiàn)了超越專家的預(yù)測。

對單個專家降噪

定理3：如果數(shù)據(jù)是由單個帶噪聲的專家生成的，那么存在某個溫度??在 (0, 1) 范圍內(nèi)，使得對于所有不超過??的??′，預(yù)測器能夠?qū)崿F(xiàn)超越。

在單一專家提供的數(shù)據(jù)中，即使存在噪聲，通過低溫采樣也能夠?qū)崿F(xiàn)超越。

多專家超越

定理4：如果測試分布??test不是集中在單一子集Xi上，即至少有兩個不同的子集滿足??test(????)>0和??test(????)>0，那么在低溫采樣下，通過??1,…,????生成的數(shù)據(jù)可以實現(xiàn)超越。

只要測試分布不是只關(guān)注一個專家擅長的子集，而是涵蓋了多個子集，那么通過低溫采樣，就可以實現(xiàn)超越。這是因為低溫采樣有助于集中概率質(zhì)量在更可能的預(yù)測上，從而提高整體性能。

實驗結(jié)果

研究的核心問題是探討「低溫采樣是否能夠在實踐中真正引發(fā)超越現(xiàn)象」。

為了回答這個問題，研究人員測試了定理2，通過評估不同溫度值下的多個ChessFormer模型，測試溫度值的范圍變化從0.001（接近確定性）到1.0（原始分布），再到1.5（高熵）。

在圖1中，作者明確證實了超越現(xiàn)象的存在。ChessFormer 1000和ChessFormer 1300模型在溫度τ等于0.001時能夠?qū)崿F(xiàn)大約1500的等級評分，展現(xiàn)出了超越現(xiàn)象。

通過調(diào)整采樣溫度，模型能夠在某些情況下超越它們在訓(xùn)練期間所見過的最高等級。

研究人員還提出了兩個問題來深入理解超越現(xiàn)象：獎勵函數(shù)如何隨低溫采樣而變化，以及超越是否依賴于數(shù)據(jù)集的多樣性。

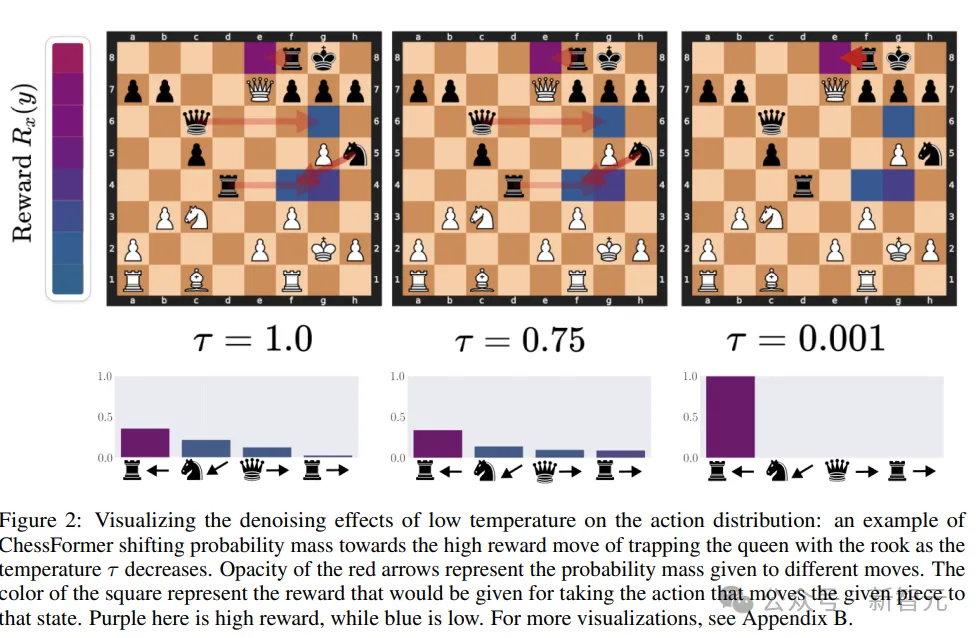
在棋類游戲中，技術(shù)水平較低的玩家可能在關(guān)鍵時刻犯下重大錯誤。如果這些錯誤具有個體差異，通過多個專家的預(yù)測平均化可以產(chǎn)生去噪效果，從而提高最佳走法的概率。

低溫采樣可以將概率質(zhì)量轉(zhuǎn)移到特定游戲情境中的更好走法上，從而提高預(yù)期獎勵。

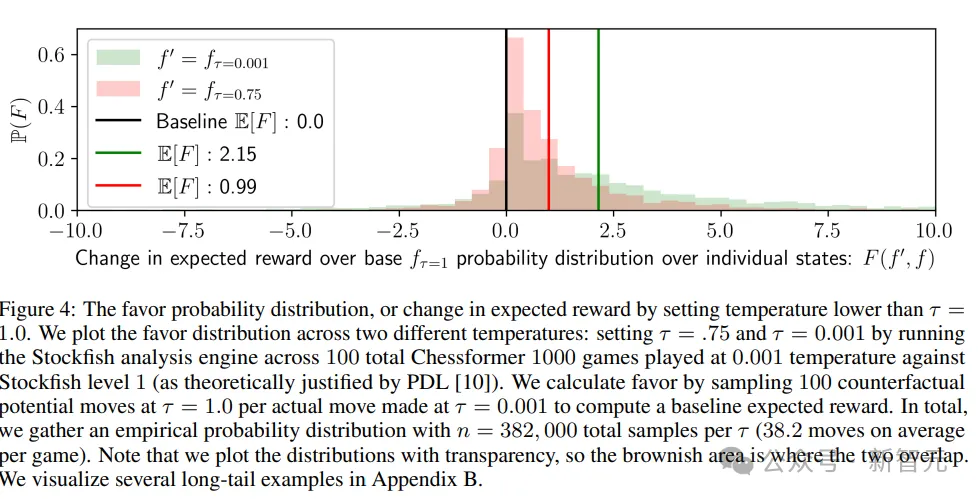
總之，實驗和可視化結(jié)果強調(diào)了通過低溫采樣實現(xiàn)超越現(xiàn)象的潛力，并提出了研究問題來探索這一現(xiàn)象背后的機制。