在信息爆炸的互聯網時代，應如何根據重要性對搜索得到的網頁進行排名并呈現給用戶？

這個問題困擾了無數早期的搜索引擎。

破局者來自Google，創始人Sergey Brin和Lawrence Page提出的網頁排名算法PageRank為這個難題提供了一個開創性的解決方案：為每個網頁都計算了一個重要性得分，即PageRank得分，得分越高表示該網頁質量越好，在信息檢索時的重要性越高。

因此，在給用戶反饋網頁搜索結果時，此類重要網頁應被排在更前面，以期用戶具有較好的搜索體驗。

考慮到互聯網的龐大規模，「如何高效地計算出互聯網上各網頁的PageRank得分？」，這一問題自PageRank提出后便受到了研究者的長期關注，所研究問題大致可分為兩類：

1. 計算互聯網上所有網頁的PageRank得分，更通用地，如果將互聯網中的網頁鏈接結構轉化為一個圖結構，網頁對應圖節點，網頁間的鏈接關系對應節點間的連邊，此類問題即希望高效地計算出圖上所有節點的PageRank得分；

2. 與之相對地，另一類問題關注互聯網上少量特定網頁的PageRank得分計算，例如，計算某幾個知名網站的PageRank得分，這類問題被稱為單點PageRank計算（single-node PageRank）。

對于上述兩類問題，第一類的研究已基本成熟，但第二類「單點PageRank計算」的計算復雜度還遠未至最優。

最近，中國人民大學的研究人員在2024年的ACM計算理論年會（ACM Symposium on Theory of Computing，STOC）上發表了一篇論文將單點PageRank的計算復雜度優化至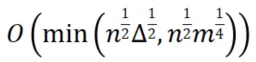級別，同時給出了與之相匹配的理論下界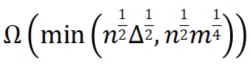，證明了其所提復雜度上下界的最優性。

圖片

論文鏈接：https://arxiv.org/abs/2403.12648

論文的所有作者均來自人大，包括魏哲巍教授、文繼榮教授、博士生王涵之和楊銘基。

這項研究解決了單點PageRank計算這一有著多年研究歷史的難題，但其所給出的達到最優計算復雜度的理論證明卻十分簡潔。

幾位STOC審稿人如此評價道：

「文中給出的證明出奇得短而簡潔，卻又是難以想到的，這令我感到吃驚。」

「這篇文章用十分精巧的分析解決了一個已被大量研究的問題。」

PageRank定義思想

Google最初基于如下兩點給出了網頁PageRank得分的計算方式：

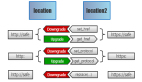
1. 大家普遍傾向于引用質量較高的網頁，如果一個網頁被大量網頁所引用，其質量應較好，故應提高其PageRank得分，從而提高其在搜索結果中的排名；

2. 另一方面，若一個網頁已知較為重要（如知名機構的官網），則其所引用的網頁也應較為重要。故一個PageRank得分較高的網頁所引用的網頁也應具有較高的PageRank得分，在搜索結果中的排名也應較高。

圖片

由此，Google將各網頁的初始PageRank得分都設為1，再根據上述兩點規則對各網頁的PageRank得分進行迭代更新直至各網頁的PageRank得分收斂，從而以一種簡潔而優雅的方式完成了互聯網上網頁重要性的量化，有效提高了Google搜索引擎的檢索質量。

PageRank算法具有簡潔的定義形式和良好的數學性質，其在被提出后即受到了廣泛關注，相關計算形式后被視為圖結構中節點中心性的一種重要衡量方式，被應用于網絡分析、信息檢索、推薦系統、圖神經網絡，甚至化學、生物和神經科學等領域中。PageRank也因其重要性和影響力被評為「數據挖掘十大算法」之一。

單點PageRank計算

單點PageRank計算作為PageRank研究中的一類重要問題，期望對互聯網上一小部分目標網頁的PageRank得分進行高效計算。

自2004年起，學者們就開始嘗試以亞線性復雜度為目標進行算法設計，即希望在不獲取整個互聯網結構的情況下完成計算。

這里之所以強調亞線性時間復雜度，是因為當今互聯網的規模過大，但傳統的PageRank迭代算法需要對整個網絡進行若干輪迭代計算直至各個網頁的PageRank指標收斂，而在大數據時代海量的網頁面前，這種全局迭代算法的計算代價變得難以忍受，也與該問題的輸出大小（即幾個目標網頁的PageRank分值）差距過大。

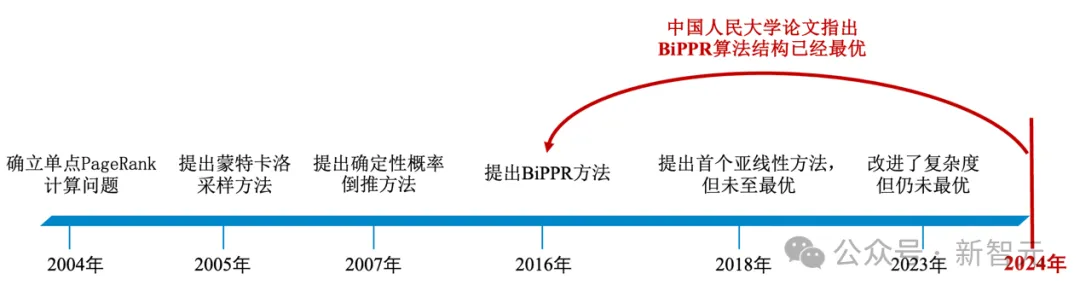
然而，單點PageRank的計算直至2018年才首次有亞線性時間的算法被提出，且算法結構非常復雜，所得計算復雜度與該問題的理論下界間仍有一定差距，未達到理論最優。

中國人民大學的研究改進了單點PageRank問題的計算復雜度，將該問題的計算復雜度優化至理論最優，與該問題計算復雜度的理論下界完全匹配。

更有意思的是，這篇論文所給出的最優復雜度結果，是對一個提出于2016年WSDM論文上的算法BiPPR進行計算復雜度重新分析得到的。

圖片

具體而言，在單點PageRank計算中，有兩個常用的基礎算子：蒙特卡洛采樣（Monte Carlo Sampling）和確定性概率倒推（簡稱Push算法），分別于2005年和2007年提出。

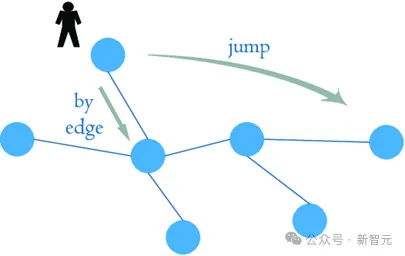
其中，蒙特卡洛采樣的思路是將單點PageRank計算轉化為隨機游走概率估計。此處隨機游走對應的一個直觀的動態過程：想象一名用戶在互聯網上沖浪，其隨機點開一個網頁進行瀏覽，在瀏覽過程中可能沿該網頁中內嵌的鏈接進行網頁跳轉，亦可能在瀏覽到某網頁時結束上網沖浪。

可以證明，互聯網上任意一個網頁t的PageRank分值，即等于一名用戶在互聯網上隨意瀏覽網頁時，瀏覽到網頁t且在瀏覽網頁t后即結束上網沖浪這一事件發生的概率。

圖片

借助PageRank的上述概率含義，蒙特卡洛采樣方法的思路為：在互聯網上重復網頁瀏覽過程多次，記錄瀏覽到網頁且在瀏覽網頁后即結束上網沖浪這一事件發生的次數，用該次數占網頁瀏覽過程重復次數的比例，作為對網頁的PageRank得分的估計。

蒙特卡洛采樣方法簡潔、直接，是單點PageRank計算的基礎方法，但其劣勢為，在估計較小的PageRank分值會消耗大量的時間。在蒙特卡洛采樣方法之后，來自UCSD、微軟、康奈爾、波士頓大學的學者Andersen、Borgs、Chayes、Hopcroft、Mirrokni和Teng在2007年提出了單點PageRank計算的另一個重要方法：確定性概率倒推（多被稱為Push算法）。

確定性概率倒推方法可被理解為蒙特卡洛采樣中隨機游走的逆過程，其擅長估計較小的PageRank分值，與蒙特卡洛采樣方法優勢互補。但確定性概率倒推方法的計算復雜度分析始終缺乏有意義的結論，為此，Andersen、Borgs、Chayes、Hopcroft、Mirrokni和Teng還在其論文的最后留下了開放性問題，希望在確定性概率倒推的計算復雜度分析方面有所突破。

2016年，斯坦福大學和康奈爾大學的三名學者Lofgren、Banerjee和Goel在WSDM會議上提出了BiPPR算法，其核心思想是給出了蒙特卡洛采樣和確定性概率倒推兩個基礎方法的一種巧妙的結合方式，以期兼容二者優勢。但是，由于確定性概率倒推計算復雜度的缺乏有意義的結果，BiPPR算法在最壞情況下的計算復雜度亦不明朗。

在BiPPR方法被提出之后，研究者們多次嘗試改進BiPPR算法，其中最具代表性的是來自意大利羅馬大學和帕多瓦大學的三名學者Bressan、Peserico、Pretto于2018年FOCS會議上提出的算法，其將蒙特卡洛采樣和確定性倒推方法各自復雜化，并修改了兩個方法的結合方式，最終得到了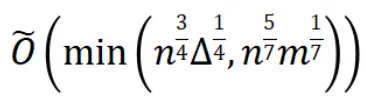的計算復雜度結果，其中n和m分別為圖節點數和邊數、?為圖節點最大出度，此處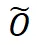表示隱去了對數因子的大O表示法。該復雜度結果是首個亞線性級別（即o(m+n)級別）的單點PageRank計算復雜度結果。

但是，得到該復雜度的算法結構非常復雜，且與計算復雜度下界之間存在較大差距。2023年，該復雜度被進一步優化至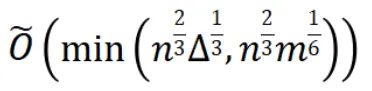，但算法結構仍然復雜，與理論下界間仍有差距。

老算法新分析：基礎算法的巧妙結合與簡潔分析

中國人民大學今年的這篇STOC論文重新分析了2016年提出的BiPPR算法的計算復雜度，證明其復雜度可被約束為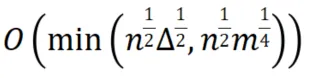級別。同時，人大這篇論文還給出了與其復雜度上界相匹配的理論下界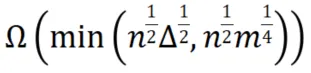，證明其復雜度結果達到了理論最優。

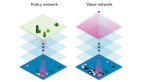
該論文的核心思路可以概括為兩點：其一，蒙特卡洛采樣和確定性概率倒推兩個基礎方法優勢互補，如果能將二者巧妙地結合起來，則可以有效提高該問題的計算效率；其二，BiPPR算法已經給出了一種很好的結合蒙特卡洛采樣和確定性概率倒推的方法，之所以之前未得到理想的復雜度結論，主要在于確定性概率倒推方法的計算復雜度不清晰。

由此，人大STOC論文首先對確定性概率倒推方法在最壞情況下的計算復雜度進行了分析，首次給出了有效的復雜度結果，同時證明了所得復雜度的最優性，從而回答了Andersen、Borgs、Chayes、Hopcroft、Mirrokni和Teng在2007年提出的關于確定性概率倒推方法計算復雜度的開放性問題。

該論文進一步將該復雜度分析用于對BiPPR方法的計算復雜度分析中，最終解決了單點PageRank計算這一有著多年研究歷史的難題。

參考資料：

https://arxiv.org/abs/2403.12648