7B參數的Qwen2.5數學推理表現超過o1-preview，這是怎么做到的？！

靠的就是MSRA最新的創(chuàng)新算法，rStar-Math。

通過代碼增強CoT、蒙特卡洛樹搜索（MCTS）等，rStar-Math能讓小·大模型在不依賴蒸餾教師模型的情況下，通過多輪自我進化的深度思維，掌握數學推理。

并且戰(zhàn)功赫赫：

在美國數學競賽AIME 2024測試中，rStar-Math平均解決了53.3%的難題（OpenAI o1-preview為44.6%），打敗所有其它開源大模型，一舉成為最聰明的高中生數學top20%。

在MATH基準測試中，rStar-Math將阿里開源大模型Qwen2.5-Math-7B的準確率，從58.8%拉升到90.0%；Qwen2.5-Math-1.5B的準確率從51.2%拉升到87.8%；Phi3-mini-3.8B的準確率從41.4%提高到86.4%

——這些成績全部全部超過了OpenAI o1-preview。

就說牛不牛吧！

小聲說，微軟最近有一股在小·大模型圈子里重拳出擊的態(tài)勢：昨天剛開源了目前最強的小·大模型，14B的phi-4；今天又推出了rStar-Math，論文中直指其面向小語言模型（SLM）。

這個趨勢剛有點苗頭，立刻引得全網討論連連。

有網友不禁開始猜測：

咱就是說，有沒有一種可能，在固定計算預算的情況下，小·大模型其實在某些推理問題上，它就是搶過大模型呢？

rStar - Math怎么做到的？

Let’s 提問：

讓小語言模型能和o1的數學推理能力相媲美甚至超越，且無需從高級教師模型中蒸餾，它怎么做到的？

MSRA在論文中表示，這是通過蒙特卡洛樹搜索（MCTS）進行深度思考來實現的，并且，其中一個數學策略小模型在基于小模型的過程獎勵模型的指導下執(zhí)行測試時搜索。

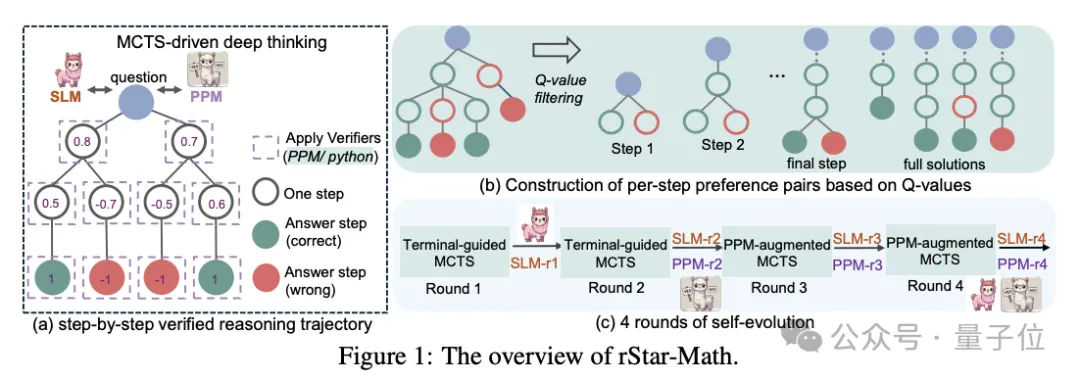
目前，業(yè)界普遍依賴自然語言生成的推理步驟來提升數學推理模型的能力。

這種方法很直給，但其關鍵在于訓練一個強大的策略模型來生成解決方案步驟，還需要訓練一個可靠的獎勵模型來進行準確評估。

然而上述兩個模型都依賴于高質量的訓練數據。

眾所周知的壞消息是，高質量的數學推理數據在現在是非常非常稀缺的，同時高質量的合成數據也存在一定bug。

而且實驗過程表明，它容易造成許多不相關、不必要的步驟，或產生錯誤。

當這種浪費和失誤出現在復雜的數學問題中時，一般很難被察覺。

現有的辦法，比如基于蒸餾的數據合成方法來訓練策略模型（如擴大GPT-4蒸餾的CoT數據），已經明顯的出現回報遞減，且最終展現的能力無法超過其他教師模型。

與此同時，截至今天，訓練可靠的PRM（Process Reward Model，過程獎勵模型）進行數學推理仍然是一個懸而未決的問題。

MSRA此次推出的rStar-Math，就引入了三項創(chuàng)新方法，來應對訓練兩個小模型的挑戰(zhàn)：

• 代碼增強CoT數據合成方法
• 過程獎勵模型訓練方法
• 四輪自我思維深度進化

咱展開來說說～

代碼增強CoT數據合成方法

rStar-Math選擇使用代碼增強CoT來解決上述難題。

該方法執(zhí)行廣泛的MCTS部署，從而生成具有自我注釋的MCTS Q值的逐步驗證推理軌跡。

具體來說，一個數學問題的求解，會在MCTS內被分解為多步生成。

模型在生成每一步推理時，作為策略模型的哪個SLM會對候選節(jié)點進行采樣，不僅生成這一步的CoT思維臉解釋，還生成相對應的Python代碼。

為了驗證生成質量，只有成功執(zhí)行Python代碼的節(jié)點才會被保留，從而減少中間步驟的錯誤，確保每一步推理的正確性。

在此基礎上，為了進一步確保推理步驟的質量，rStar-Math使用了MCTS來生成逐步推理軌跡（用來分解復雜的數學問題為多個單步生成任務）。

大量的MCTS回滾會根據每個中間步驟對最終正確答案的貢獻，自動為其分配一個Q值。

有助于產生更多導致正確答案的軌跡的步驟將被賦予更高的Q值，并被認為具有更高的質量。

這確保了SLM生成的推理軌跡，是由正確、高質量的中間步驟組成的。

過程獎勵模型訓練方法

現階段，多數大模型在解決推理數學問題時，都面臨一個問題：

無法無法提供細粒度的步驟級反饋，以幫助其在推理過程中做出更優(yōu)的選擇。

盡管使用了廣泛的MCTS部署，仍會出現Q值不夠精確的情況，這就導致無法對每個推理步驟進行評分。

為此，rStar-Math通過引入用于訓練充當過程偏好模型（PPM，Process Preference Model）的SLM，來可靠地為每個數學推理步驟預測獎勵標簽。

PPM的核心思想，是通過構建步驟級的正負偏好對來訓練模型，而不是直接依賴于精確的步驟級評分。

它根據Q值為每個步驟構建偏好對，并使用成對排名損失來優(yōu)化PPM對每個推理步驟的分數預測，實現可靠的標記。

如上所述，Q值雖然不精準、含噪聲，但PPM可以利用它，可靠地區(qū)分正（正確）步驟和負（不相關 / 錯誤）步驟。

四輪自我思維深度進化

由于SLM能力較大模型更弱，團隊設計了四輪自我思維深度進化，以逐步生成更高質量的數據，并通過更具挑戰(zhàn)性的數學問題擴展訓練集。

值得注意的是，團隊首先選擇了一個包含747k個數學問題的開源數據集。

但在每一輪中，研究團隊沒有使用747k數學數據集中的原始解決方案，而是進行了廣泛的MCTS部署——

四輪中的每一輪，都使用MCTS生成逐步驗證的推理軌跡，然后將其用于訓練新策略SLM和PPM；然后又在下一輪中應用新模型，以生成更高質量的訓練數據。

四輪自我思維深度進化具體如下。

第一輪：

通過監(jiān)督微調對基礎模型進行初步改進，為后續(xù)的自我進化奠定基礎。

改進后的模型表示為SLM-r1。

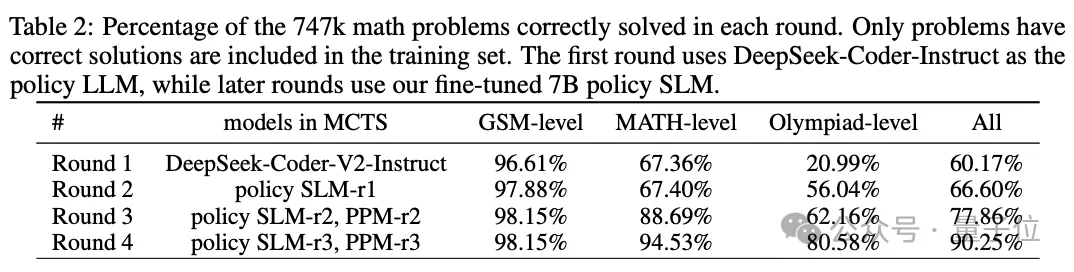
如表2所示，研究人員使用DeepSeek-Coder-V2-Instruct （236B）運行MCTS來收集SFT數據。

由于本輪沒有可用的獎勵模型，研究者對Q值使用終端引導的注釋，并將MCTS限制為8次推出，以提高效率。

為了獲得正確的解決方案，團隊選擇具有最高平均Q值的前2條軌跡作為SFT數據。

同時，團隊在這一輪中也訓練了PPM-r1。

這一輪的關鍵在于生成高質量的初始訓練數據，并利用這些數據對基礎模型進行微調。

第二輪：

訓練可靠的PPM-r2，通過PPM顯著提升模型推理能力。

在這一輪中，隨著策略模型更新到7B SLM-r1，團隊進行了廣泛的MCTS部署，以獲得更可靠的Q值注釋；除此之外，還訓練了第一個可靠的獎勵模型PPM-r2。

具體來說，研究團隊為每個問題執(zhí)行16次MCTS部署。由此產生的逐步驗證推理軌跡表明，質量和Q值精度都有了顯著提高。

如表 4 所示，PPM-r2明顯比bootstrap輪次更有效。

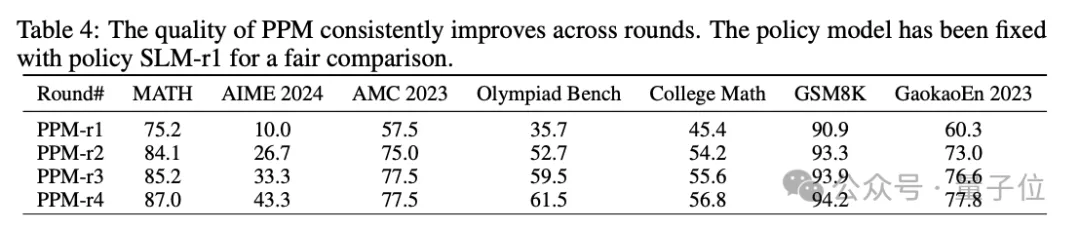
此外，如表3所示，策略模型SLM-r2也如預期的那樣繼續(xù)改進，指導其在后續(xù)的推理中做出更好的選擇。

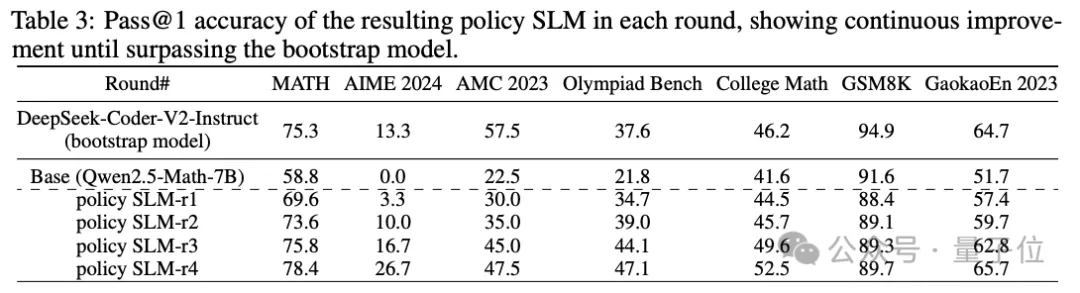
第三輪：

通過PPM增強的MCTS生成更高質量的數據，進一步提升模型的推理能力。

借助可靠的PPM-r2，研究人員在這一輪中執(zhí)行PPM增強的MCTS以生成數據，從而獲得更高質量的軌跡。此處涵蓋訓練集中的更多數學和奧林匹克級別問題（詳細可見表2）。

然后，研究者使用生成的推理軌跡和自我注釋的Q值，來訓練新策略SLM-r3和PPM-r3——這兩者都顯示出顯著的改進。

第四輪：

通過增加MCTS回滾次數，解決具有挑戰(zhàn)性的數學難題。

前第三輪后，雖然rStar - Math已經讓SLM在小學和MATH題目上提高成功率，但奧賽級別題目成績還是只有62.16%。

為此，團隊采用了一種簡單的策略，即對于在16次MCTS部署后未解決的問題，會額外執(zhí)行64次部署。

如果需要，這個次數可以增加到128次。

此外，研究者們還使用不同的隨機種子進行多個MCTS擴展，最后將奧賽級別問題的成功率提高到80.58%。

△此處再貼一次表2，方便大家查閱

綜上，經過四輪自我進化，747k數學題的成績已經來到了90.25%。

剩下的未解決的問題中，很大一部分都是綜合問題。

研究者人工手動審查了20個問題的隨機樣本，發(fā)現其中19個問題被錯誤地標記為錯誤答案。

基于此，團隊得出結論：剩余的未解決的問題質量較低，因此自我進化的腳步終止在第4輪。

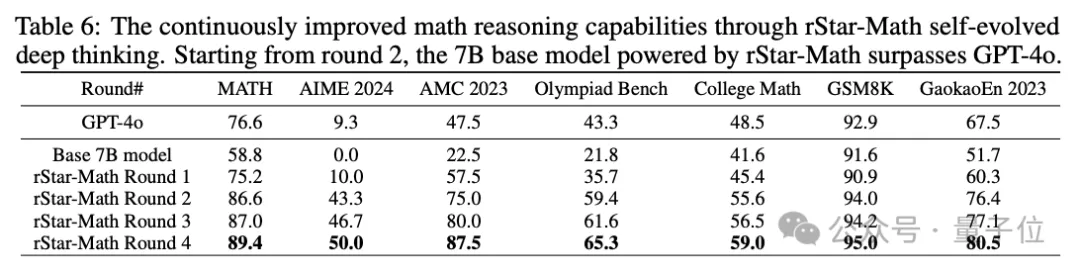
實驗評估與發(fā)現

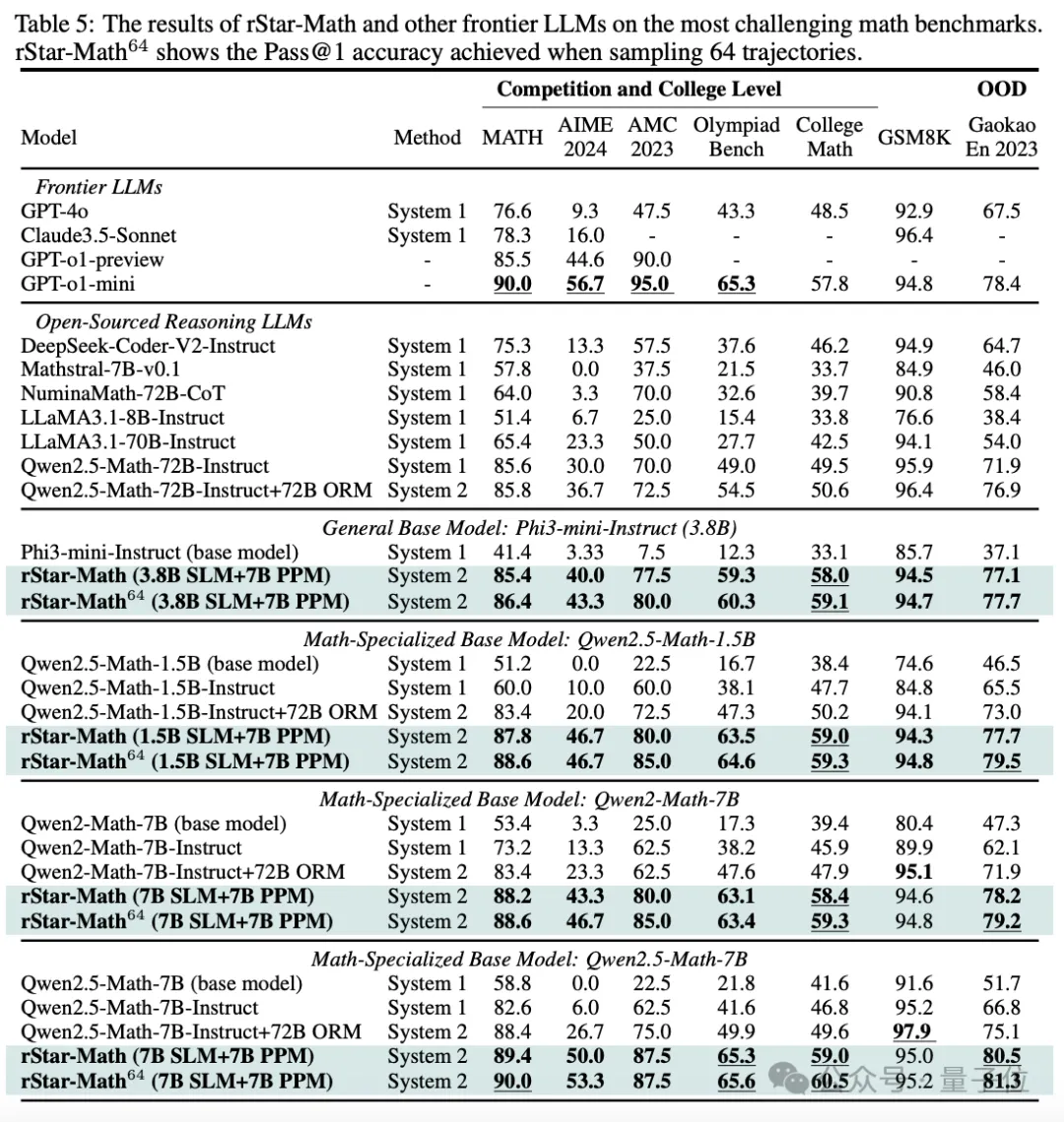
下面的表5，顯示了rStar-Math與最先進的推理模型進行比較的結果。

有三個值得說道說道的觀察發(fā)現：

第一，rStar-Math 顯著提高了SLM的數學推理能力，以小得多的模型尺寸，實現了與OpenAI o1相當，甚至超過o1的性能。

例如，Qwen2.5-Math-7B最初在MATH上的準確率為58.8%，使用rStar-Math后，準確率顯著提高到90.0%，優(yōu)于o1-preview和Claude 3.5 Sonnet，和o1-mini打了個平手。

在College Math基準測試中，rStar-Math后Qwen2.5-Math-7B的比o1-mini高出 2.7%。

在AIME 2024上，rStar-Math后的Qwen2.5-Math-7B得分為53.3%，不及o1-mini的56.7%。不過，7B模型在AIME I 和 II 中解決了8/15的問題，在最聰明的高中數學學生中排名前 20%。

而未解決的問題中，有8個是需要視覺里覺的幾何圖形題，這個功能目前rStar-Math還不支持。

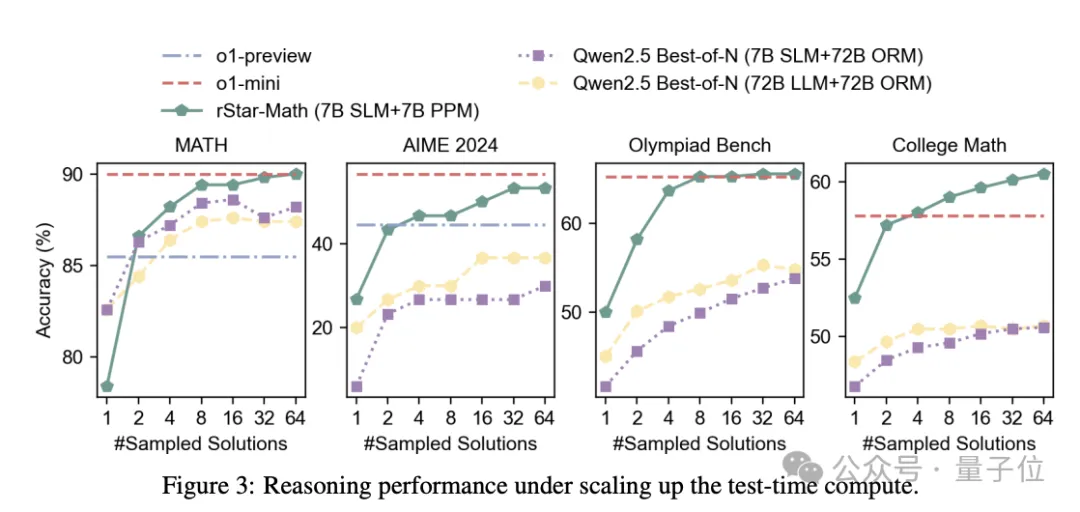
第二，盡管使用較小的政策模型（1.5B-7B）和獎勵模型（7B），但rStar-Math的性能明顯優(yōu)于最先進的System 2基線。

與使用相同的基本模型（Qwen2-Math-7B、Qwen2.5-Math-1.5B/7B）但獎勵模型 （Qwen2.5-Math-RM-72B） 大10倍以上的Qwen Best-of-N基線相比，rStar-Math始終將所有基本模型的推理準確性提高到最先進的水平。

即使與Qwen2.5-Math-72B-Instruct的策略模型大10倍以上的N-Best-of-N對比，使用相同數量的采樣解決方案，rStar-Math也在除GSM8K之外的所有基準測試中也超過了它。

第三，除了MATH、GSM8K和AIME等可能存在過度優(yōu)化的知名基準測試之外，rStar-Math在其它具有挑戰(zhàn)性的數學基準測試中表現出很強的通用性。

包括但不限于奧賽基準、大學數學和中國高考數學考試 （Gaokao）。

而且需要強調的是，rStar-Math訓練集主要來自公共數據集，并沒有針對這些基準測試進行特定的優(yōu)化。

總的來說，實驗結果驗證了自進化、逐步驗證推理軌跡和PPM的有效性。

One More Thing

本研究的共同一作分別是MSRA的Xinyu Guan和Li Lyna Zhang。

Li Lyna Zhang是工作的項目leader，本博都畢業(yè)于中國科學技術大學，目前是MSRA系統與網絡組的高級研究員。

另一位共同一作，Xinyu Guan，在完成這項工作的時候是MSRA的實習生，這位同學當時還在北大讀書。

BTW，論文中另一位作者Youran Sun參與項目時也是MSRA實習生，這位同學則是清華er。

啊，年輕人的世界，又是實習生呢～

arXiv：https://arxiv.org/pdf/2501.04519

代碼和數據詳見GitHub：https://github.com/microsoft/rStar