中山大學、美團聯合團隊推出行為正則化與順序策略優化結合的離線多智能體學習算法
離線多智能體強化學習(MARL)是一個新興領域,目標是在從預先收集的數據集中學習最佳的多智能體策略。相比于單智能體情況,多智能體環境涉及到大規模的聯合狀態-動作空間和多智能體間的耦合行為,這給離線策略優化帶來了額外的復雜性。隨著人工智能技術的發展,多智能體系統在諸如自動駕駛、智能家居和機器人協作等方面展現了巨大的應用潛力。但是離線MARL較單智能體情況下更加復雜,其涉及龐大的聯合狀態-動作空間和多智能體間的復雜互動行為,這使得離線策略優化成為一項艱巨的任務。
離線MARL面臨的主要挑戰包括:一是如何有效應對分布偏移問題,即在策略評估過程中,分布外(OOD)樣本可能導致誤差積累;二是在多智能體環境下,協調多個智能體的行為顯得尤為困難。現有的離線MARL方法盡管取得了一些進展,但仍存在不協調行為和分布外聯合動作的問題。為了應對這些挑戰,來自中山大學、美團的聯合團隊提出了一種新穎的離線MARL算法——樣本內順序策略優化(In-Sample Sequential Policy Optimization, InSPO),該方法通過順序更新每個智能體的策略,避免選擇OOD聯合動作,同時增強了智能體之間的協調。
12月 11 日,arXiv發表了他們的技術論文《Offline Multi-Agent Reinforcement Learning via In-Sample Sequential Policy Optimization》。研究團隊的主要貢獻在于提出了InSPO算法,該算法不僅避免了OOD聯合動作,還通過探索行為策略中的低概率動作,解決了提前收斂到次優解的問題。理論上InSPO保證了策略的單調改進,并收斂到量化響應均衡(QRE)。實驗結果表明,InSPO在多個離線MARL任務中表現出了顯著的效果,與當前最先進的方法相比具有明顯的優勢。
研究團隊成員又來自中山大學計算機科學與工程學院的Zongkai Liu, Qian Lin, Chao Yu和Xiawei Wu、上海創新研究院的Zongkai Liu和美團的Yile Liang, Donghui Li和Xuetao Ding,涵蓋了學術界和工業界的專家,致力于多智能體強化學習和行為優化等領域的研究。
合作型馬爾可夫游戲
在理解離線多智能體強化學習(MARL)中的樣本內順序策略優化之前,首先需要了解合作型馬爾可夫游戲的基本概念和框架。

圖1:XOR游戲。(a) 是聯合行動的獎勵矩陣。(b) 是數據集的分布。
定義與基本概念
合作型馬爾可夫游戲是一種多智能體系統的建模方法,它能夠有效地描述多個智能體在同一環境中進行交互的過程。這個游戲模型定義為G=?N,S,A,P,r,γ,d?G = \langle N, S, A, P, r, \gamma, d \rangle。其中,NN是智能體的集合,SS是有限的狀態空間,AA是聯合動作空間,包含了所有智能體的動作集合。轉移概率函數PP描述了從一個狀態到另一個狀態的轉移可能性,公共獎勵函數rr則為所有智能體提供統一的獎勵反饋。折扣因子γ\gamma和初始狀態分布dd分別影響未來獎勵的權重和初始狀態的選擇。在每一個時間步tt,每個智能體ii在狀態sts_t選擇動作aita_i^t,并依次移動到下一個狀態st+1s_{t+1},同時根據聯合動作接收獎勵。
IGM原則與值分解
在多智能體系統中,直接計算聯合Q函數是一個極其復雜的問題,因為狀態-動作空間會隨著智能體數量的增加而指數級增長。值分解方法通過將聯合Q函數分解為每個智能體的個體Q函數,極大地簡化了這個計算過程。具體來說,聯合Q函數Q(s,a)Q(s, a)被表示為每個智能體Q函數QiQ_i的組合。這種分解方式依賴于個體-全局-最大化(IGM)原則,即最優聯合動作可以通過每個智能體的貪婪動作來識別。然而,這種方法在處理環境中存在多模態獎勵景觀時可能會遇到困難,因為IGM假設往往會被破壞。

圖2:M-NE游戲。(a) 是聯合行動的獎勵矩陣。(b) 是數據集的分布。
離線MARL中的行為正則化馬爾可夫游戲
為了有效應對離線MARL中的分布偏移問題,行為正則化馬爾可夫游戲引入了一個與數據相關的正則化項。這個正則化項通過在獎勵函數中加入額外的懲罰,迫使學習到的策略盡量接近行為策略,從而避免選擇分布外的動作。在這個框架中,策略的目標是最大化期望折扣回報,同時減去正則化項,以此平衡策略的探索和利用。這樣不僅提高了策略的穩定性,還能防止其收斂到局部最優解。
通過引入這些基礎概念和原理,合作型馬爾可夫游戲為多智能體系統的行為建模和優化提供了一個強大的工具。尤其在離線環境中,結合行為正則化和值分解方法,可以有效解決多智能體間的協調問題,并提高策略的整體表現。
樣本內順序策略優化
在離線多智能體強化學習(MARL)中,策略的優化往往面臨著分布外(OOD)聯合動作和局部最優解問題。為了應對這些挑戰,研究團隊提出了一種創新的方法——樣本內順序策略優化(In-Sample Sequential Policy Optimization, InSPO)。該方法在行為正則化馬爾可夫游戲框架下進行,結合了逆KL散度和最大熵正則化,旨在通過順序更新每個智能體的策略,避免選擇OOD聯合動作,同時增強智能體之間的協調。
樣本內順序策略優化的數學推導
InSPO方法的核心在于通過逆KL散度進行行為正則化,從而確保學習到的策略與行為策略共享相同的支持集,避免選擇分布外的動作。具體來說,目標函數中的逆KL散度項可以分解為各個智能體的獨立項,這使得順序更新每個智能體的策略成為可能。數學上通過使用Karush-Kuhn-Tucker(KKT)條件,推導出目標函數的閉式解,從而實現樣本內學習。最終的優化目標為最小化KL散度,以確保策略更新的有效性和一致性。
最大熵行為正則化馬爾可夫游戲
為了進一步增強探索性,防止策略過早收斂到局部最優解,InSPO引入了最大熵行為正則化馬爾可夫游戲(MEBR-MG)框架。在這個框架中,策略優化的目標函數不僅包含逆KL散度項,還引入了策略熵項。通過這種方式,優化目標能夠促使策略在高概率動作和低概率動作之間保持平衡,鼓勵充分探索低概率動作,從而避免局部最優解。理論上,最大熵行為正則化還能夠確保策略收斂到量化響應均衡(QRE),即在面對擾動獎勵時,策略仍能維持穩定的性能。
通過上述方法,樣本內順序策略優化不僅有效解決了離線MARL中的OOD聯合動作問題,還通過策略熵的引入,顯著提高了策略的探索能力和全局最優解的發現概率。
算法細節
算法 1: InSPO 的步驟
InSPO算法的核心在于通過順序更新的方式,逐步優化每個智能體的策略,最終實現全局最優。具體步驟如下:
- 輸入:離線數據集DD、初始策略π0\pi_0和初始Q函數Q0Q_0。
- 輸出:最終策略πK\pi_K。
- 首先,通過簡單的行為克隆方法計算出行為策略μ\mu。
- 接下來,開始迭代優化。在每一輪迭代中,先計算出當前Q函數QkQ_k。
- 隨機抽取一個智能體的排列i1:Ni_{1:N},并依次更新每個智能體的策略。
- 對于每個智能體,使用推導出的目標函數進行策略更新。
- 重復上述過程,直到達到預定的迭代次數KK。
這種順序更新的策略,確保了每一步的策略優化都是在樣本內進行的,避免了分布外動作的選擇,提高了策略的穩定性和有效性。
策略評估
策略評估是InSPO算法中的一個關鍵步驟。根據更新的Q函數,計算當前策略的期望回報。在多智能體環境中,由于聯合動作空間的龐大,研究團隊采用了局部Q函數來進行近似。在策略評估過程中,需要順序地更新每個智能體的局部Q函數,使其能反映最新的策略信息。具體的目標函數包括一個權重項,用于平衡策略的探索和利用。此外,為了降低重要性采樣比率的高方差,InSPO采用了重要性重采樣技術,通過概率比例重采樣構建新的數據集,從而穩定算法的訓練效果。
策略改進
在獲得優化的局部Q函數后,接下來就是策略改進步驟。通過最小化KL散度,InSPO能夠在保持行為策略特性的同時,逐步優化每個智能體的策略。在具體操作中,使用推導出的目標函數來指導每個智能體的策略更新,這一過程確保了策略的收斂性和改進性。
實際應用及實現細節
在實際應用中,InSPO不僅需要在理論上保證策略的有效性,還需要在大規模狀態-動作空間中保持高效的計算性能。為了實現這一點,我們對算法進行了多方面的優化:
局部Q函數的優化:為了避免聯合動作空間的指數級增長,我們使用局部Q函數來近似全局Q函數,并通過順序更新的方法逐步優化每個智能體的局部Q函數。
重要性重采樣:通過重要性重采樣技術,構建新的數據集,降低采樣比率的方差,提高訓練的穩定性。
自動調節溫度參數α:為了找到合適的保守程度,我們實現了自動調節α的機制,根據目標值進行動態調整,從而進一步提高性能。
這些優化措施使得InSPO在處理復雜的多智能體任務時,能夠保持高效的性能和良好的收斂性。通過這些實際應用和實現細節,InSPO展現了其在離線MARL中的巨大潛力和應用價值。
實驗驗證
在M-NE游戲中,研究團隊評估了InSPO對局部最優收斂問題的緩解能力。實驗使用兩個數據集:一個是由均勻策略收集的平衡數據集,另一個是由接近局部最優的策略收集的不平衡數據集。結果顯示,在平衡數據集上,大多數算法都能找到全局最優解,而在不平衡數據集上,只有InSPO正確識別出全局最優解。這表明,在存在多個局部最優解的環境中,數據集分布對算法收斂性有顯著影響。InSPO通過全面探索數據集,避免了次優解的影響,展現了其強大的全局最優解識別能力。
橋游戲的實驗結果
橋游戲是一個類似于時間版本XOR游戲的網格世界馬爾可夫游戲。在這個實驗中,我們使用了兩個數據集:optimal數據集和mixed數據集。optimal數據集包含了由最優確定性策略生成的500條軌跡,而mixed數據集則包括optimal數據集和由均勻隨機策略生成的額外500條軌跡。實驗結果表明,只有InSPO和AlberDICE在這兩個數據集上都達到了近乎最優的性能。相比之下,值分解方法未能收斂,并產生了不理想的結果。這進一步證明了InSPO在復雜多智能體任務中的有效性。

圖3:數據集XOR博弈的最終聯合策略(b)。
星際爭霸II微操作基準測試的實驗結果
為了進一步驗證InSPO的性能,研究團隊將研究擴展到星際爭霸II微操作基準測試,這是一個高維復雜的環境。實驗使用了四個代表性地圖,并采用了四個不同的數據集:medium、expert、medium-replay和mixed。在這些實驗中,盡管值分解方法在該環境中表現出色,InSPO依然展示了其競爭力,在大多數任務中取得了最先進的結果。實驗結果證明了InSPO在高維復雜環境中的應用潛力。

表1-4:星際爭霸II微管理的平均測試獲勝率。
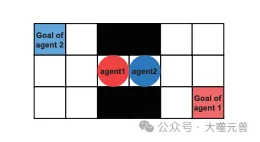
圖4:開始時的橋。
消融研究
為了評估InSPO中不同組件的影響,研究團隊進行了消融研究。首先他們在不平衡數據集上的M-NE游戲中測試了去除熵項的InSPO,結果顯示沒有熵擾動的InSPO無法逃離局部最優。他們在XOR游戲中測試了同時更新而非順序更新的InSPO,由于更新方向的沖突,未能學習到最優策略,并面臨OOD聯合動作問題。此外,研究團隊還評估了溫度參數α對策略保守程度的影響,結果表明自動調節的α能夠找到合適的值,進一步提升性能。

圖5:熵消融和順序更新方案。(a) 對于不平衡數據集,在M-NE博弈中沒有熵的InSPO。(b) 是數據集(b)XOR游戲上InSPO的同步更新版本。
通過這些實驗驗證,InSPO展現了其在解決離線MARL中的局部最優收斂問題、增強策略探索能力和提高全局最優解識別能力方面的優勢。實驗結果不僅證明了InSPO的理論可行性,還展示了其在實際應用中的強大潛力。
結論
在本研究中,研究團隊提出了一種新穎的離線多智能體強化學習(MARL)算法——樣本內順序策略優化(In-Sample Sequential Policy Optimization, InSPO)。通過引入逆KL散度和策略熵,他們有效地解決了離線MARL中的分布外(OOD)聯合動作和局部最優解問題。理論分析和實驗驗證表明,InSPO不僅能夠實現策略的單調改進,并最終收斂到量化響應均衡(QRE),還在多個基準測試中展示了優越的性能。與現有的離線MARL方法相比,InSPO在應對復雜多智能體任務、提高策略穩定性和探索能力方面具有顯著優勢。
盡管InSPO在離線MARL領域取得了突破性的進展,但仍有許多值得進一步探索的方向。
算法擴展與優化:未來可以考慮將InSPO與其他先進的MARL算法相結合,進一步提升策略優化的效果。同時,研究如何在更大規模、更復雜的環境中實現高效的策略優化,也是一個重要的方向。
數據集增強與生成:在離線MARL中,數據集的質量和分布對算法性能有著直接影響。未來可以探索通過生成對抗網絡(GANs)等技術生成高質量的數據集,從而改善策略學習的效果。
多模態獎勵景觀的應對:在存在多個局部最優解的環境中,如何更有效地識別和收斂到全局最優解,仍是一個具有挑戰性的問題。研究新的正則化方法和優化策略,能夠進一步提升InSPO的魯棒性。
實際應用與驗證:將InSPO應用到更多實際場景中,如智能交通系統、自動駕駛和智能制造等,驗證其在真實環境中的性能和穩定性,將是未來的重要研究方向。
通過這些方向的深入研究與探索,我們有望進一步提升離線MARL算法的性能和應用價值,推動人工智能技術在多智能體系統中的廣泛應用。(END)
參考資料:https://arxiv.org/abs/2412.07639

















