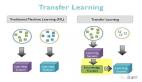
令人著迷的無梯度神經網絡優化方法
梯度下降是機器學習中最重要的思想之一:給定一些代價函數以使其最小化,該算法迭代地采取最大下降斜率的步驟,理論上在經過足夠的迭代次數后才達到最小值。柯西(Cauchy)于1847年首次發現,在1944年針對非線性優化問題在Haskell Curry上得到擴展,梯度下降已用于從線性回歸到深度神經網絡的各種算法。
雖然梯度下降及其反向傳播形式的重新用途已成為機器學習的最大突破之一,但神經網絡的優化仍然是一個尚未解決的問題。互聯網上的許多人都愿意宣稱"梯度下降很爛",盡管可能有些遙遠,但梯度下降確實存在許多問題。
優化程序陷入了足夠深的局部最小值中。誠然,有一些聰明的解決方案有時可以解決這些問題,例如動量,它可以使優化器在大山丘上行走。隨機梯度下降;或批量歸一化,從而平滑錯誤空間。但是,局部最小值仍然是神經網絡中許多分支問題的根本原因。
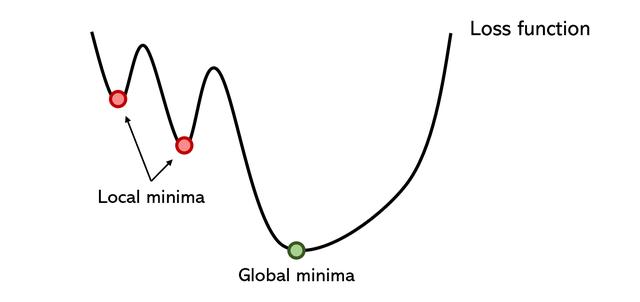
因為優化器對本地極小值很感興趣,所以即使設法擺脫它,也要花費很長時間。梯度下降法通常是一種冗長的方法,因為它的收斂速度慢,即使對大數據集(如批梯度下降法)進行了調整也是如此。
梯度下降對優化器的初始化特別敏感。例如,如果優化器在第二個局部最小值而不是第一個局部最小值附近初始化,則性能可能會好得多,但這都是隨機確定的。
學習率決定了優化器的信心和風險。設置過高的學習率可能會導致它忽略全局最小值,而過低的學習會導致運行時間中斷。為了解決這個問題,學習率隨著迭代衰減,但是在許多指示學習率的變量中選擇衰減率是困難的。
梯度下降需要梯度,這意味著它除了無法處理不可微的函數外,還容易出現基于梯度的問題,例如消失或爆炸的梯度問題。
當然,已經對梯度下降進行了廣泛的研究,并且提出了許多建議的解決方案,其中一些解決方案是GD變體,而其他解決方案是基于網絡體系結構的。僅僅因為梯度下降被高估了并不意味著它不是當前可用的最佳解決方案。即使使用批處理規范化來平滑錯誤空間或選擇復雜的優化器(如Adam或Adagrad),這些通用知識也不是本文的重點,即使它們通常表現更好。
取而代之的是,本文的目的是向一些晦澀難懂的確定性有趣的優化方法提供一些理所應得的信息,這些方法不適合基于梯度的標準方法,該方法與任何其他用于改善該方法性能的技術一樣。神經網絡在某些情況下表現特別出色,而在其他情況下則表現不佳。無論他們在特定任務上的表現如何,他們對于機器學習的未來都充滿著魅力,創造力和充滿希望的研究領域。
粒子群優化PSO
粒子群優化是一種基于種群的方法,它 定義了一組探索搜索空間并試圖尋找最小值的"粒子"。PSO相對于某個質量指標迭代地改進了候選解決方案。它通過擁有大量潛在的解決方案("粒子")并根據簡單的數學規則(例如粒子的位置和速度)移動它們來解決該問題。每個粒子的運動都受到其認為最佳的局部位置的影響,但也被搜索位置(由其他粒子找到)中最知名的位置所吸引。從理論上講,該群體經過多次迭代以求出最佳解決方案。
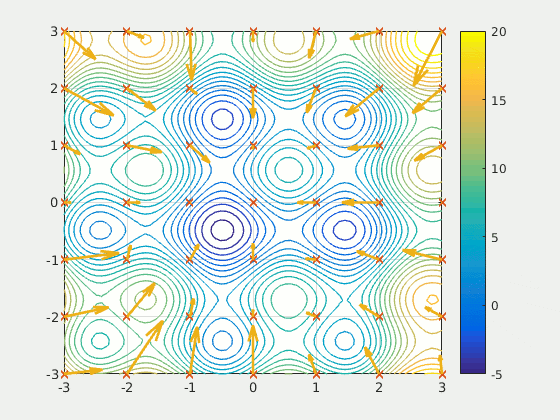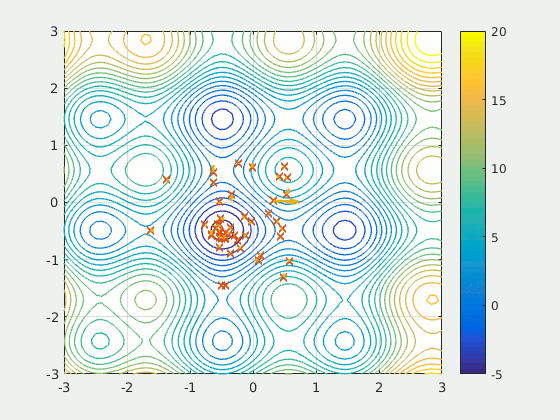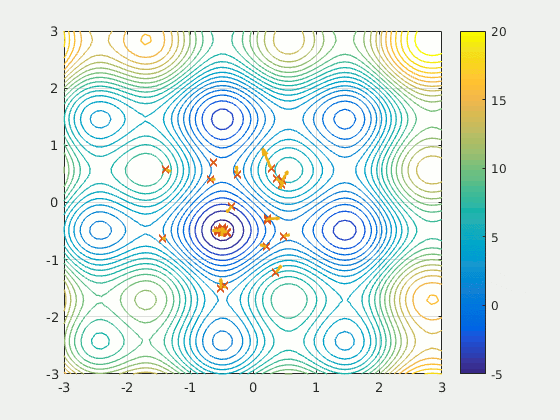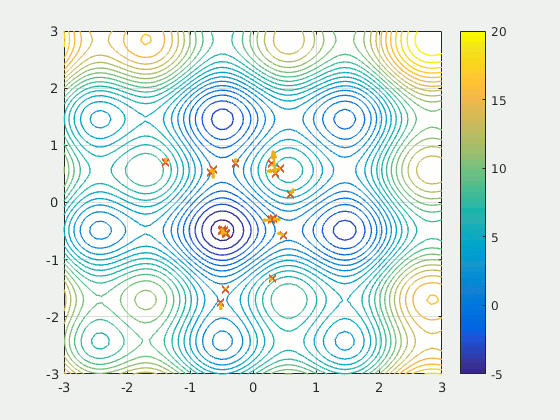
資料來源:維基
PSO是一個有趣的想法-與神經網絡相比,它對初始化的敏感度要低得多,并且在某些發現上的粒子之間的通信可能被證明是一種搜索稀疏和大面積區域的非常有效的方法。
因為粒子群優化不是基于梯度的(gasp!),所以不需要優化問題是可微的。因此,使用PSO優化神經網絡或任何其他算法將對選擇其他函數中的激活函數或等效角色具有更大的自由度和更低的敏感性。此外,它幾乎沒有關于優化問題的假設,甚至可以搜索很大的空間。
可以想象,基于總體的方法比基于梯度的優化器在計算上要昂貴得多,但不一定如此。由于該算法是如此開放和非剛性-正如基于進化的算法通常如此,因此人們可以控制粒子的數量,粒子的移動速度,全局共享的信息量等等。就像可能會調整神經網絡中的學習率一樣。
代理優化是一種優化方法,它嘗試使用另一個完善的函數對損失函數建模以找到最小值。該技術從損失函數中采樣"數據點",這意味著它嘗試使用不同的參數值(x)并存儲損失函數的值(y)。在收集到足夠數量的數據點之后,將代理函數(在這種情況下為7次多項式)擬合到所收集的數據。
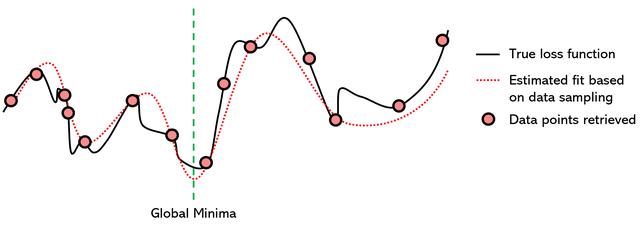
因為找到多項式的最小值是一個經過充分研究的主題,并且存在許多使用導數來找到多項式的全局最小值的非常有效的方法,所以我們可以假定替代函數的全局最小值對于損失是相同的函數。
代理優化從技術上講是一種非迭代方法,盡管代理功能的訓練通常是迭代的。此外,從技術上講,它是一種無梯度方法,盡管查找建模函數全局最小值的有效數學方法通常基于導數。但是,由于迭代和基于梯度的屬性都是替代優化的"次要"屬性,因此它可以處理大數據和不可微的優化問題。
使用代理函數的優化在以下幾種方面的特性:
- 它實質上是在平滑真實的損失函數的表面,從而減少了鋸齒狀的局部最小值,該局部最小值導致了神經網絡中大量額外的訓練時間。
- 它將一個困難的問題投影到一個容易得多的問題上:無論是多項式,RBF、GP、MARS還是其他替代模型,尋找全局最小值的任務都會借助數學知識來完成。
- 過擬合替代模型并不是什么大問題,因為即使有相當多的過擬合,替代函數也比真實損失函數更平滑,參差不齊。除了建立簡化的數學傾向模型外,還有許多其他標準考慮因素,因此訓練替代模型要容易得多。
- 替代優化不受當前位置的限制,因為它看到了"整個函數",而不是梯度下降,梯度下降必須不斷做出危險的選擇,以決定是否認為下一個山峰會有更深的最小值。
替代優化幾乎總是比梯度下降方法快,但通常以準確性為代價。使用代理優化可能只能查明全局最小值的大致位置,但這仍然可以極大地受益。
另一種方法是混合模型。替代優化用于將神經網絡參數帶到粗略位置,從中可以使用梯度下降法找到確切的全局最小值。另一個方法是使用替代模型來指導優化程序的決策,因為替代函數可以a)"先見之明"和b)對損失函數的特定起伏不敏感。
模擬退火
模擬退火是基于冶金退火的概念,其中可以將材料加熱到其重結晶溫度以上,以降低其硬度并改變其他物理特性,有時還改變化學特性,然后使材料逐漸冷卻并再次變硬。
使用緩慢冷卻的概念,隨著對溶液空間的探索,模擬退火緩慢地降低了接受較差溶液的可能性。由于接受較差的解決方案可以對全局最小值進行更廣泛的搜索(認為-越過山丘進入更深的山谷),因此模擬退火假定可以在第一次迭代中正確表示和探索各種可能性。隨著時間的流逝,該算法從探索轉向開發。
以下是模擬退火算法如何工作的粗略概述:
- 溫度設置為某個初始正值,然后逐漸接近零。
- 在每個時間步長上,算法都會隨機選擇一個與當前解決方案接近的解決方案,測量其質量,然后根據當前溫度(接受更好或更差的解決方案的可能性)移至該解決方案。
- 理想情況下,當溫度達到零時,該算法已收斂于全局最小解。
可以使用動力學方程式或隨機采樣方法進行模擬。模擬退火用于解決旅行商問題,該問題試圖找到數百個位置之間的最短距離,以數據點表示。顯然,這些組合是無止境的,但是模擬退火(加上強化學習的效果)效果很好。
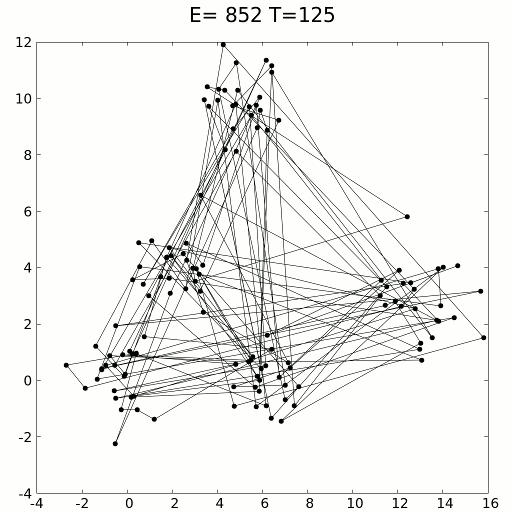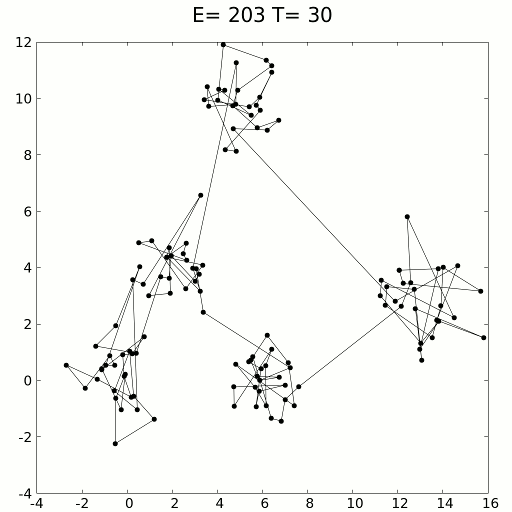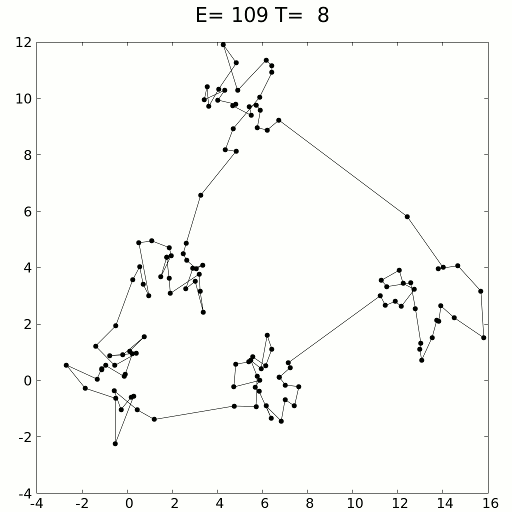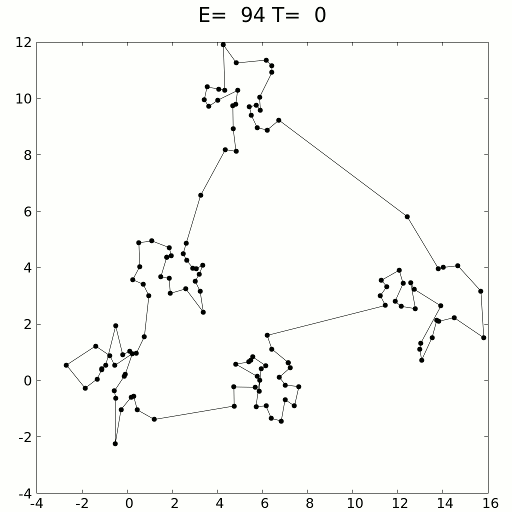
模擬的旅行商問題退火解決方案。資料來源:維基
在需要在短時間內找到近似解的情況下,模擬退火效果特別好,勝過緩慢的梯度下降速度。像代理優化一樣,它可以與梯度下降混合使用,從而具有以下優點:模擬退火的速度和梯度下降的準確性。
這是一些非梯度方法的樣本;還有許多其他的算法,例如模式搜索和多目標優化,都需要探索。鑒于我們人類遺傳成功的證據,因此基于遺傳和種群的算法(例如粒子群優化)對于創建真正的"智能"代理非常有前途。
非梯度優化方法之所以令人著迷,是因為它們很多都利用了創造力,而不受梯度數學鏈的限制。沒有人期望無梯度方法能夠成為主流,因為即使考慮到許多問題,基于梯度的優化也能如此出色。但是,將無梯度和基于梯度的方法的強大功能與混合優化器一起使用證明了極高的潛力,特別是在我們達到計算極限的時代。