[[441004]]

給定一個二叉樹，我們在樹的節(jié)點上安裝攝像頭。

節(jié)點上的每個攝影頭都可以監(jiān)視其父對象、自身及其直接子對象。

計算監(jiān)控樹的所有節(jié)點所需的最小攝像頭數量。

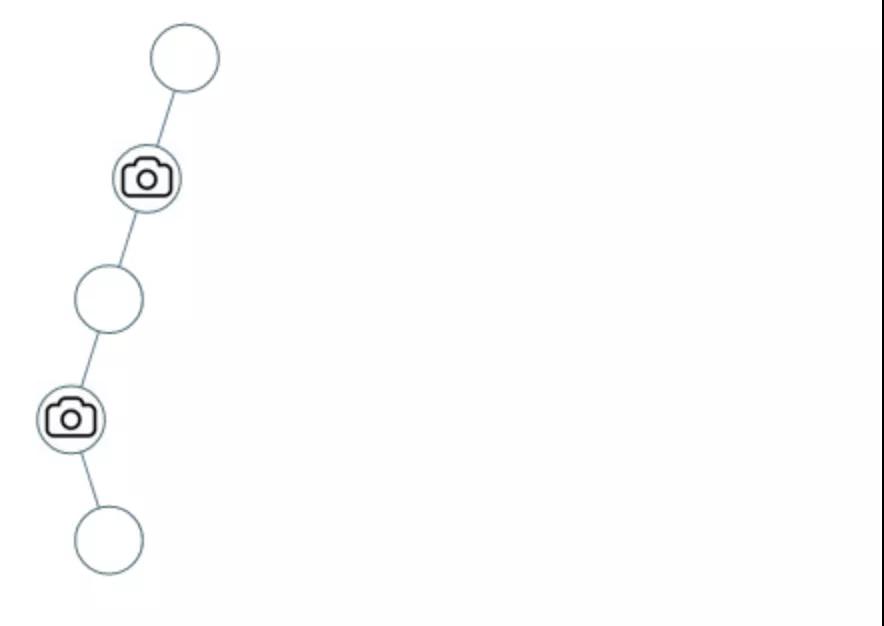
示例 1：

• 輸入：[0,0,null,0,0]
• 輸出：1
• 解釋：如圖所示，一臺攝像頭足以監(jiān)控所有節(jié)點。

示例 2：

• 輸入：[0,0,null,0,null,0,null,null,0]
• 輸出：2
• 解釋：需要至少兩個攝像頭來監(jiān)視樹的所有節(jié)點。上圖顯示了攝像頭放置的有效位置之一。

提示：

• 給定樹的節(jié)點數的范圍是 [1, 1000]。
• 每個節(jié)點的值都是 0。

思路

這道題目首先要想，如何放置，才能讓攝像頭最小的呢?

從題目中示例，其實可以得到啟發(fā)，我們發(fā)現題目示例中的攝像頭都沒有放在葉子節(jié)點上!

這是很重要的一個線索，攝像頭可以覆蓋上中下三層，如果把攝像頭放在葉子節(jié)點上，就浪費的一層的覆蓋。

所以把攝像頭放在葉子節(jié)點的父節(jié)點位置，才能充分利用攝像頭的覆蓋面積。

那么有同學可能問了，為什么不從頭結點開始看起呢，為啥要從葉子節(jié)點看呢?

因為頭結點放不放攝像頭也就省下一個攝像頭， 葉子節(jié)點放不放攝像頭省下了的攝像頭數量是指數階別的。

所以我們要從下往上看，局部最優(yōu)：讓葉子節(jié)點的父節(jié)點安攝像頭，所用攝像頭最少，整體最優(yōu)：全部攝像頭數量所用最少!

局部最優(yōu)推出全局最優(yōu)，找不出反例，那么就按照貪心來!

此時，大體思路就是從低到上，先給葉子節(jié)點父節(jié)點放個攝像頭，然后隔兩個節(jié)點放一個攝像頭，直至到二叉樹頭結點。

此時這道題目還有兩個難點：

• 二叉樹的遍歷
• 如何隔兩個節(jié)點放一個攝像頭

確定遍歷順序

在二叉樹中如何從低向上推導呢?

可以使用后序遍歷也就是左右中的順序，這樣就可以在回溯的過程中從下到上進行推導了。

后序遍歷代碼如下：

int traversal(TreeNode* cur) { 
 
    // 空節(jié)點，該節(jié)點有覆蓋 
    if (終止條件) return ; 
 
    int left = traversal(cur->left);    // 左 
    int right = traversal(cur->right);  // 右 
 
    邏輯處理                            // 中 
    return ; 
} 

注意在以上代碼中我們取了左孩子的返回值，右孩子的返回值，即left 和 right， 以后推導中間節(jié)點的狀態(tài)

如何隔兩個節(jié)點放一個攝像頭

此時需要狀態(tài)轉移的公式，大家不要和動態(tài)的狀態(tài)轉移公式混到一起，本題狀態(tài)轉移沒有擇優(yōu)的過程，就是單純的狀態(tài)轉移!

來看看這個狀態(tài)應該如何轉移，先來看看每個節(jié)點可能有幾種狀態(tài)：

有如下三種：

• 該節(jié)點無覆蓋
• 本節(jié)點有攝像頭
• 本節(jié)點有覆蓋

我們分別有三個數字來表示：

• 0：該節(jié)點無覆蓋
• 1：本節(jié)點有攝像頭
• 2：本節(jié)點有覆蓋

大家應該找不出第四個節(jié)點的狀態(tài)了。

一些同學可能會想有沒有第四種狀態(tài)：本節(jié)點無攝像頭，其實無攝像頭就是 無覆蓋 或者 有覆蓋的狀態(tài)，所以一共還是三個狀態(tài)。

因為在遍歷樹的過程中，就會遇到空節(jié)點，那么問題來了，空節(jié)點究竟是哪一種狀態(tài)呢?空節(jié)點表示無覆蓋?表示有攝像頭?還是有覆蓋呢?

回歸本質，為了讓攝像頭數量最少，我們要盡量讓葉子節(jié)點的父節(jié)點安裝攝像頭，這樣才能攝像頭的數量最少。

那么空節(jié)點不能是無覆蓋的狀態(tài)，這樣葉子節(jié)點就要放攝像頭了，空節(jié)點也不能是有攝像頭的狀態(tài)，這樣葉子節(jié)點的父節(jié)點就沒有必要放攝像頭了，而是可以把攝像頭放在葉子節(jié)點的爺爺節(jié)點上。

所以空節(jié)點的狀態(tài)只能是有覆蓋，這樣就可以在葉子節(jié)點的父節(jié)點放攝像頭了

接下來就是遞推關系。

那么遞歸的終止條件應該是遇到了空節(jié)點，此時應該返回2(有覆蓋)，原因上面已經解釋過了。

代碼如下：

// 空節(jié)點，該節(jié)點有覆蓋 
if (cur == NULL) return 2; 

遞歸的函數，以及終止條件已經確定了，再來看單層邏輯處理。

主要有如下四類情況：

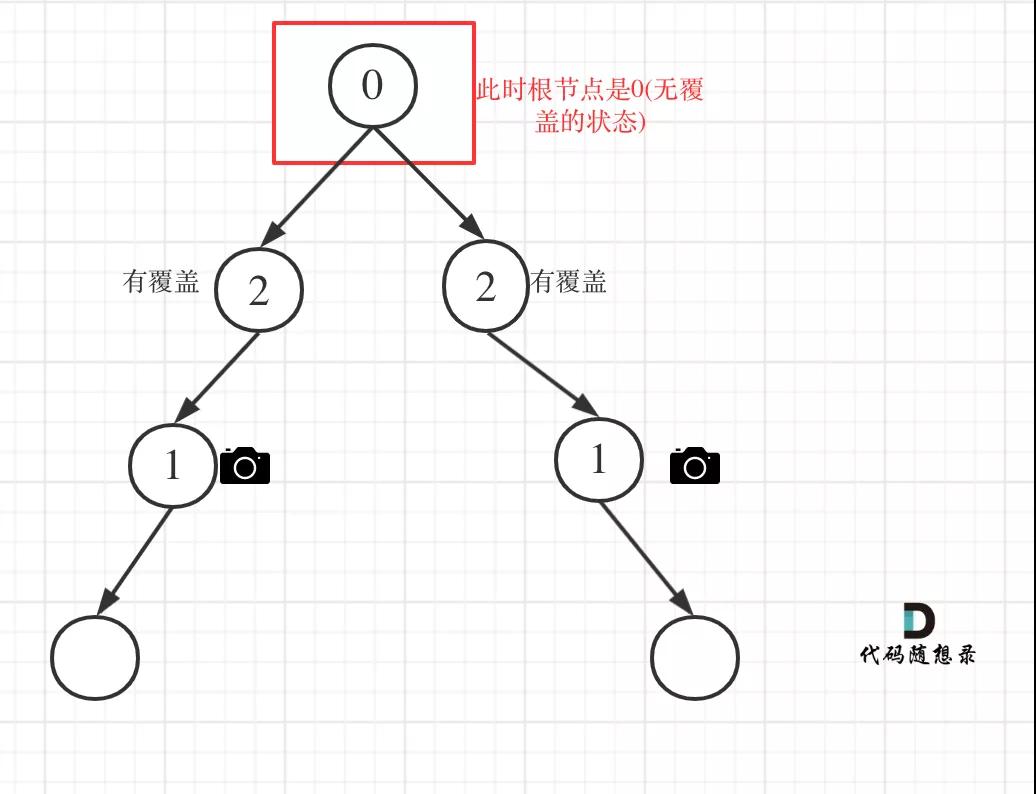
• 情況1：左右節(jié)點都有覆蓋

左孩子有覆蓋，右孩子有覆蓋，那么此時中間節(jié)點應該就是無覆蓋的狀態(tài)了。

如圖：

監(jiān)控二叉樹2

代碼如下：

// 左右節(jié)點都有覆蓋 
if (left == 2 && right == 2) return 0; 

• 情況2：左右節(jié)點至少有一個無覆蓋的情況

如果是以下情況，則中間節(jié)點(父節(jié)點)應該放攝像頭：

left == 0 && right == 0 左右節(jié)點無覆蓋 left == 1 && right == 0 左節(jié)點有攝像頭，右節(jié)點無覆蓋 left == 0 && right == 1 左節(jié)點有無覆蓋，右節(jié)點攝像頭 left == 0 && right == 2 左節(jié)點無覆蓋，右節(jié)點覆蓋 left == 2 && right == 0 左節(jié)點覆蓋，右節(jié)點無覆蓋

這個不難理解，畢竟有一個孩子沒有覆蓋，父節(jié)點就應該放攝像頭。

此時攝像頭的數量要加一，并且return 1，代表中間節(jié)點放攝像頭。

代碼如下：

if (left == 0 || right == 0) { 
    result++; 
    return 1; 
} 

• 情況3：左右節(jié)點至少有一個有攝像頭

如果是以下情況，其實就是 左右孩子節(jié)點有一個有攝像頭了，那么其父節(jié)點就應該是2(覆蓋的狀態(tài))

left == 1 && right == 2 左節(jié)點有攝像頭，右節(jié)點有覆蓋 left == 2 && right == 1 左節(jié)點有覆蓋，右節(jié)點有攝像頭 left == 1 && right == 1 左右節(jié)點都有攝像頭

代碼如下：

if (left == 1 || right == 1) return 2; 

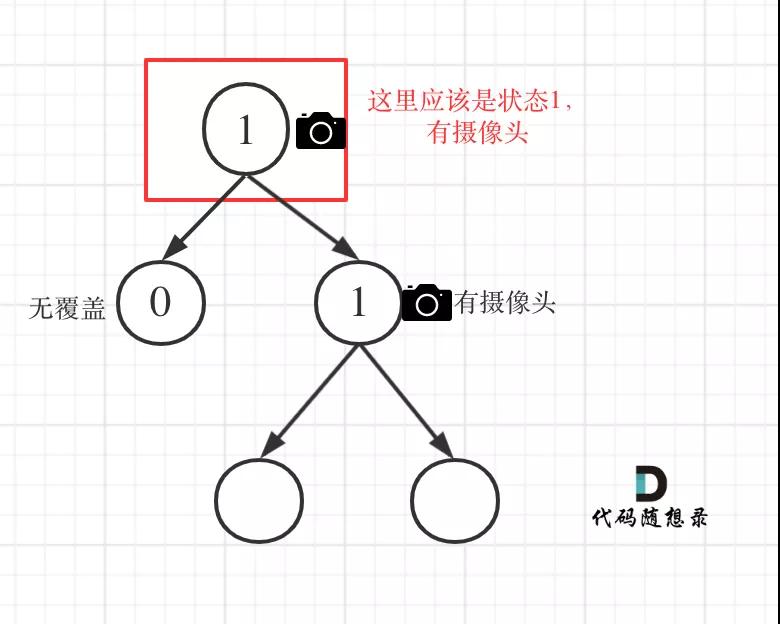
從這個代碼中，可以看出，如果left == 1, right == 0 怎么辦?其實這種條件在情況2中已經判斷過了，如圖：

監(jiān)控二叉樹1

這種情況也是大多數同學容易迷惑的情況。

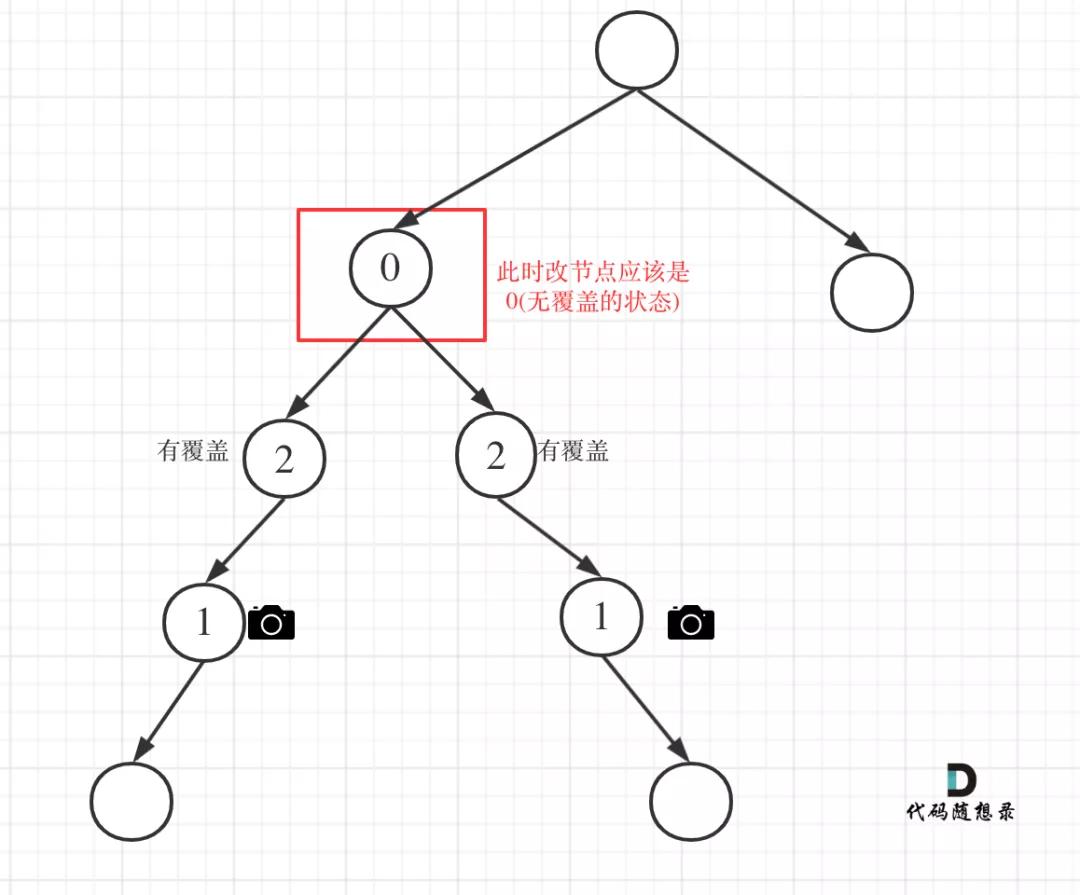
• 情況4：頭結點沒有覆蓋

以上都處理完了，遞歸結束之后，可能頭結點 還有一個無覆蓋的情況，如圖：

監(jiān)控二叉樹3

所以遞歸結束之后，還要判斷根節(jié)點，如果沒有覆蓋，result++，代碼如下：

int minCameraCover(TreeNode* root) { 
    result = 0; 
    if (traversal(root) == 0) { // root 無覆蓋 
        result++; 
    } 
    return result; 
} 

以上四種情況我們分析完了，代碼也差不多了，整體代碼如下：

(以下我的代碼注釋很詳細，為了把情況說清楚，特別把每種情況列出來。)

C++代碼如下：

// 版本一 
class Solution { 
private: 
    int result; 
    int traversal(TreeNode* cur) { 
 
        // 空節(jié)點，該節(jié)點有覆蓋 
        if (cur == NULL) return 2; 
 
        int left = traversal(cur->left);    // 左 
        int right = traversal(cur->right);  // 右 
 
        // 情況1 
        // 左右節(jié)點都有覆蓋 
        if (left == 2 && right == 2) return 0; 
 
        // 情況2 
        // left == 0 && right == 0 左右節(jié)點無覆蓋 
        // left == 1 && right == 0 左節(jié)點有攝像頭，右節(jié)點無覆蓋 
        // left == 0 && right == 1 左節(jié)點有無覆蓋，右節(jié)點攝像頭 
        // left == 0 && right == 2 左節(jié)點無覆蓋，右節(jié)點覆蓋 
        // left == 2 && right == 0 左節(jié)點覆蓋，右節(jié)點無覆蓋 
        if (left == 0 || right == 0) { 
            result++; 
            return 1; 
        } 
 
        // 情況3 
        // left == 1 && right == 2 左節(jié)點有攝像頭，右節(jié)點有覆蓋 
        // left == 2 && right == 1 左節(jié)點有覆蓋，右節(jié)點有攝像頭 
        // left == 1 && right == 1 左右節(jié)點都有攝像頭 
        // 其他情況前段代碼均已覆蓋 
        if (left == 1 || right == 1) return 2; 
 
        // 以上代碼我沒有使用else，主要是為了把各個分支條件展現出來，這樣代碼有助于讀者理解 
        // 這個 return -1 邏輯不會走到這里。 
        return -1; 
    } 
 
public: 
    int minCameraCover(TreeNode* root) { 
        result = 0; 
        // 情況4 
        if (traversal(root) == 0) { // root 無覆蓋 
            result++; 
        } 
        return result; 
    } 
}; 

在以上代碼的基礎上，再進行精簡，代碼如下：

// 版本二 
class Solution { 
private: 
    int result; 
    int traversal(TreeNode* cur) { 
        if (cur == NULL) return 2; 
        int left = traversal(cur->left);    // 左 
        int right = traversal(cur->right);  // 右 
        if (left == 2 && right == 2) return 0; 
        else if (left == 0 || right == 0) { 
            result++; 
            return 1; 
        } else return 2; 
    } 
public: 
    int minCameraCover(TreeNode* root) { 
        result = 0; 
        if (traversal(root) == 0) { // root 無覆蓋 
            result++; 
        } 
        return result; 
    } 
}; 

大家可能會驚訝，居然可以這么簡短，其實就是在版本一的基礎上，使用else把一些情況直接覆蓋掉了。

在網上關于這道題解可以搜到很多這種神級別的代碼，但都沒講不清楚，如果直接看代碼的話，指定越看越暈，所以建議大家對著版本一的代碼一步一步來哈，版本二中看不中用!。

總結

本題的難點首先是要想到貪心的思路，然后就是遍歷和狀態(tài)推導。

在二叉樹上進行狀態(tài)推導，其實難度就上了一個臺階了，需要對二叉樹的操作非常嫻熟。

這道題目是名副其實的hard，大家感受感受，哈哈。