一篇講明白對稱的二叉樹
作者：神奇的程序員
如果一顆二叉樹和它的鏡像一樣，那么它就是對稱的。實現一個函數用于判斷一顆二叉樹是否對稱，你會怎么做？本文將分享一種解決方案，歡迎各位感興趣的開發(fā)者閱讀本文。
實現思路
二叉樹的鏡像中我們知道了此問題的解決方案是前序遍歷，那么我們可以修改下前序遍歷算法，父節(jié)點遍歷后，先遍歷它的右子節(jié)點，再遍歷它的左子節(jié)點，我們把這種算法稱為：對稱前序遍歷。
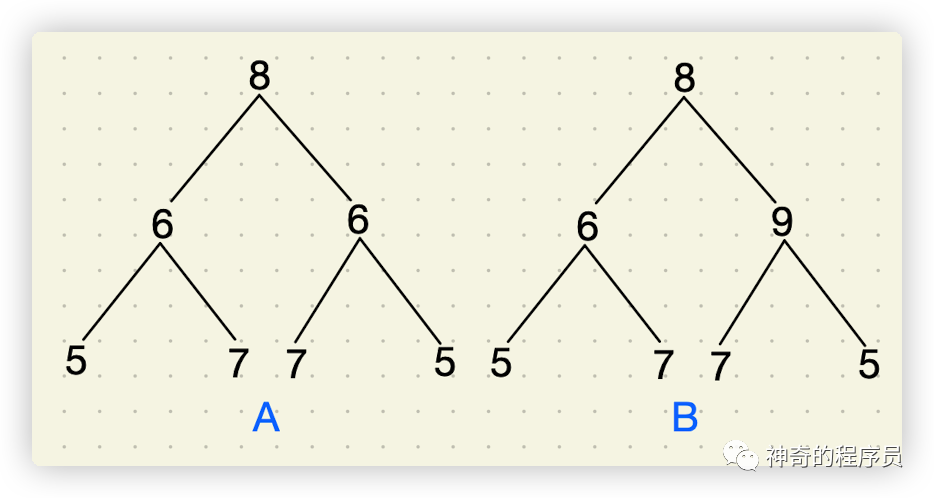
如下圖所示的兩棵樹，我們分別列舉下兩種遍歷的結果：
樹A：
- 前序遍歷：8, 6, 5, 7, 6, 7, 5
- 對稱前序遍歷：8, 6, 5, 7, 6, 7, 5
樹B：
- 前序遍歷：8, 6, 5, 7, 9, 7, 5
- 對稱前序遍歷：8, 9, 5, 7, 6, 7, 5
經過對比后，我們發(fā)現樹A的兩種遍歷方法得到的結果是一樣的，那么它就是對稱的；樹B的結果不同，它就不是對稱的。
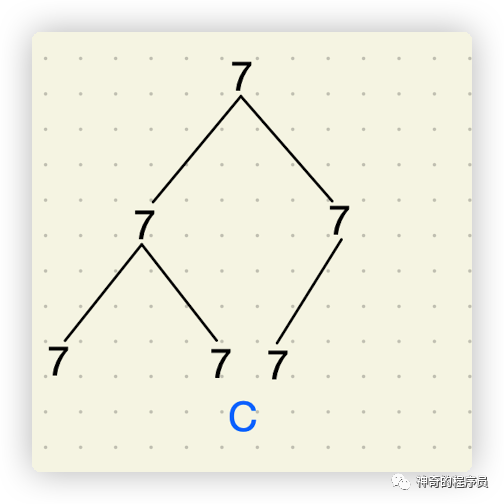
如果有一顆不完全二叉樹，它的所有節(jié)點都相同，他是對稱的嗎？
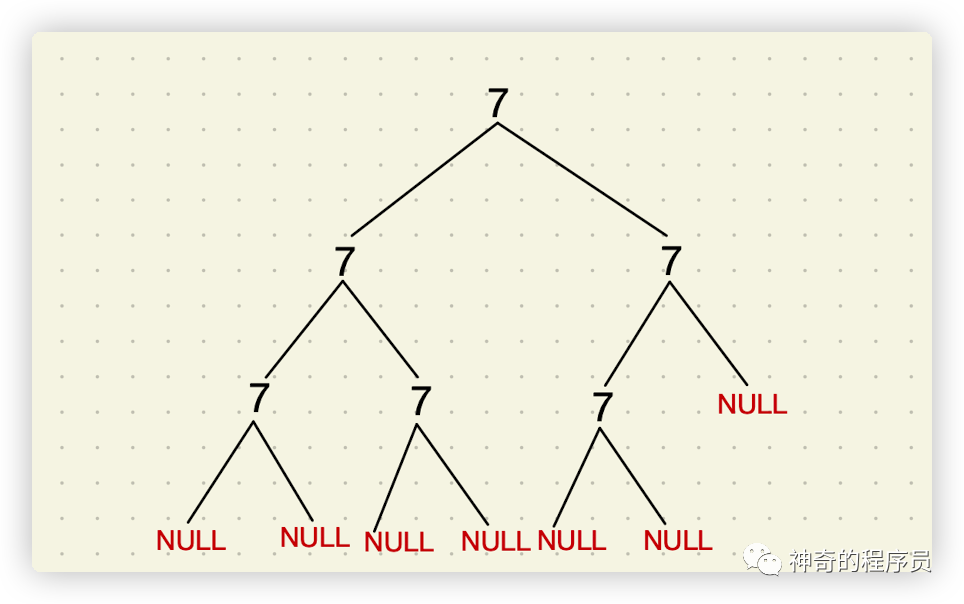
針對于這種情況，我們就需要將它缺省的null節(jié)點進行補齊了，補齊后的兩種遍歷結果為：
- 前序遍歷：7, 7, 7, null, null, 7, null, null, 7, 7, null, null, null
- 對稱前序遍歷：7, 7, null, 7, null, null, 7, 7, null, null, 7, null, null
對比兩個結果后，我們發(fā)現并不一樣，那么它就不是對稱的。
實現代碼
- 有了思路后，接下來我們看下代碼實現，如下所示：
- 從樹的根節(jié)點出發(fā)，遞歸比對它的左子節(jié)點和右子節(jié)點
比對過程中：
二者都到達葉子節(jié)點，代表這棵樹是對稱的
任意一方到達葉子結點，代表這棵樹不對稱
節(jié)點值不同，這棵樹不對稱
export function SymmetricBinaryTree(node: BinaryTreeNode | null): boolean {
return isSymmetrical(node, node);
}
function isSymmetrical(
node: BinaryTreeNode | null | undefined,
cloneNode: BinaryTreeNode | null | undefined
): boolean {
// 到達葉子節(jié)點，兩者都為nul代表節(jié)點相同
if (node == null && cloneNode == null) {
return true;
}
// 任意一方到達葉子節(jié)點，代表節(jié)點不同
if (node == null || cloneNode == null) {
return false;
}
// 節(jié)點值不同
if (node.key != cloneNode.key) {
return false;
}
// 分別比對樹的左子節(jié)點和右子節(jié)點
return (
isSymmetrical(node.left, cloneNode.right) &&
isSymmetrical(node.right, cloneNode.left)
);
}
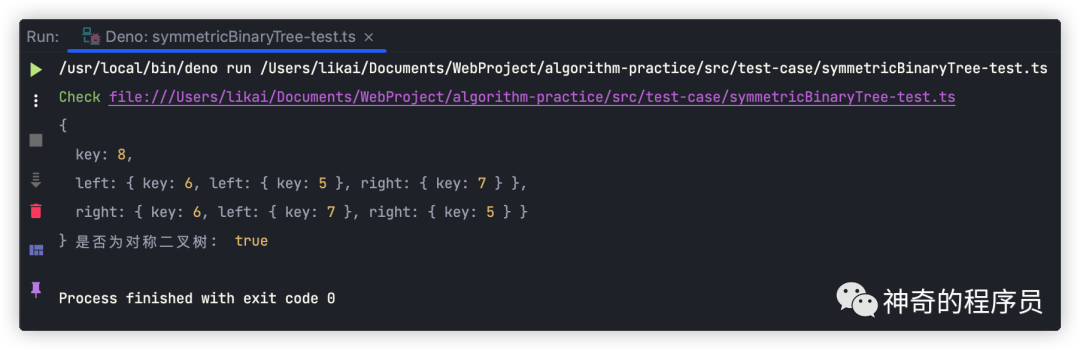
接下來，我們以上個章節(jié)列舉的例子為例，將其帶入上述代碼，驗證下能否正確判斷，如下所示：
const tree: BinaryTreeNode = {
key: 8,
left: {
key: 6,
left: { key: 5 },
right: { key: 7 }
},
right: { key: 6, left: { key: 7 }, right: { key: 5 } }
};
const isSymmetric = SymmetricBinaryTree(tree);
console.log(tree, "是否為對稱二叉樹: ", isSymmetric);
示例代碼
本文所用代碼完整版請移步：
- SymmetricBinaryTree
- symmetricBinaryTree-test.ts
責任編輯：武曉燕
來源：
神奇的程序員
