[[437293]]

本文轉載自微信公眾號「程序員千羽」，作者程序員千羽。轉載本文請聯系程序員千羽公眾號。

Leetcode : https://leetcode-cn.com/problems/er-cha-shu-de-jing-xiang-lcof

“GitHub : https://github.com/nateshao/leetcode/blob/main/algo-notes/src/main/java/com/nateshao/sword_offer/topic_21_mirrorTree/Solution.java

 二叉樹的鏡像

“題目描述 ：請完成一個函數，輸入一個二叉樹，該函數輸出它的鏡像。例如輸入：

    4 
   /   \ 
  2     7 
 / \   / \ 
1   3 6   9 

鏡像輸出：

      4 
    /   \ 
   7     2 
 / \   / \ 
9   6 3   1 

示例 1：

輸入：root = [4,2,7,1,3,6,9] 
輸出：[4,7,2,9,6,3,1] 

限制：0 <= 節點個數 <= 1000

分析

二叉樹鏡像定義： 對于二叉樹中任意節點 root ，設其左 / 右子節點分別為 left, right;則在二叉樹的鏡像中的對應 root節點，其左 / 右子節點分別為 right, left 。

方法一：遞歸法

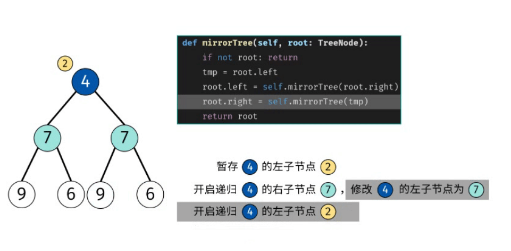
根據二叉樹鏡像的定義，考慮遞歸遍歷(dfs)二叉樹，交換每個節點的左 / 右子節點，即可生成二叉樹的鏡像。

遞歸解析：

終止條件： 當節點 root為空時(即越過葉節點)，則返回 null ;

遞推工作：

初始化節點tmp,用于暫存root的左子節點; .

開啟遞歸右子節點mirrorTree(root.right)，并將返回值作為root的左子節點。

開啟遞歸左子節點mirrorTree(tmp) ,并將返回值作為root的右子節點。

返回值:返回當前節點root ;

“Q:為何需要暫存root的左子節點? A:在遞歸右子節 點“root.left = mirrorTree(root.right);"執行完畢后，root.left 的值已經發生改變,此時遞歸左子節點mirrorTree(root.left)則會出問題。

復雜度分析:

• 時間復雜度0(N) ： 其中N為二叉樹的節點數量，建立二叉樹鏡像需要遍歷樹的所有節點，占用O(N)時間。
• 空間復雜度O(N)： 最差情況下(當二叉樹退化為鏈表)，遞歸時系統需使用O(N)大小的棧空間。

package com.nateshao.sword_offer.topic_21_mirrorTree; 
 
import java.util.Stack; 
 
/** 
 * @date Created by 邵桐杰 on 2021/11/24 22:48 
 * @微信公眾號 程序員千羽 
 * @個人網站 www.nateshao.cn 
 * @博客 https://nateshao.gitee.io 
 * @GitHub https://github.com/nateshao 
 * @Gitee https://gitee.com/nateshao 
 * Description: 劍指 Offer 27. 二叉樹的鏡像 
 */ 
public class Solution { 
    /** 
     * 遞歸 
     * 
     * @param root 
     * @return 
     */ 
    public TreeNode mirrorTree(TreeNode root) { 
        if (root == null) return null; 
        TreeNode node = root.left; 
        root.left = mirrorTree(root.right); 
        root.right = mirrorTree(node); 
        return root; 
    } 
 
    /** 
     * 解法一：遞歸，時間復雜度：O(n)，空間復雜度：O(n) 
     * 
     * @param root 
     * @return 
     */ 
    public boolean isSymmetric(TreeNode root) { 
        if (root == null) return true; 
        return isMirror(root.left, root.right); 
    } 
 
    private boolean isMirror(TreeNode leftNode, TreeNode rightNode) { 
        if (leftNode == null && rightNode == null) return true; 
        if (leftNode == null || rightNode == null) return false; 
 
        return leftNode.val == rightNode.val && isMirror(leftNode.left, rightNode.right) && isMirror(leftNode.right, rightNode.left); 
    } 
 
    public class TreeNode { 
        int val; 
        TreeNode left; 
        TreeNode right; 
 
        TreeNode(int x) { 
            val = x; 
        } 
    } 
 
} 

方法二：輔助棧(或隊列)

利用棧(或隊列)遍歷樹的所有節點node，并交換每個node的左/右子節點。

算法流程：

• 特例處理： 當root為空時，直接返回null ;
• 初始化： 棧(或隊列)，本文用棧，并加入根節點root 。
• 循環交換： 當棧 stack為控時跳出;
  • 出棧：記為node ;
  • 添加子節點：將node左和右子節點入棧;
  • 交換：交換node的左1右子節點。
• 返回值：返回根節點root。

復雜度分析:

• 時間復雜度0(N) ：其中N為二叉樹的節點數量，建立二叉樹鏡像需要遍歷樹的所有節點，占用O(N)時間。
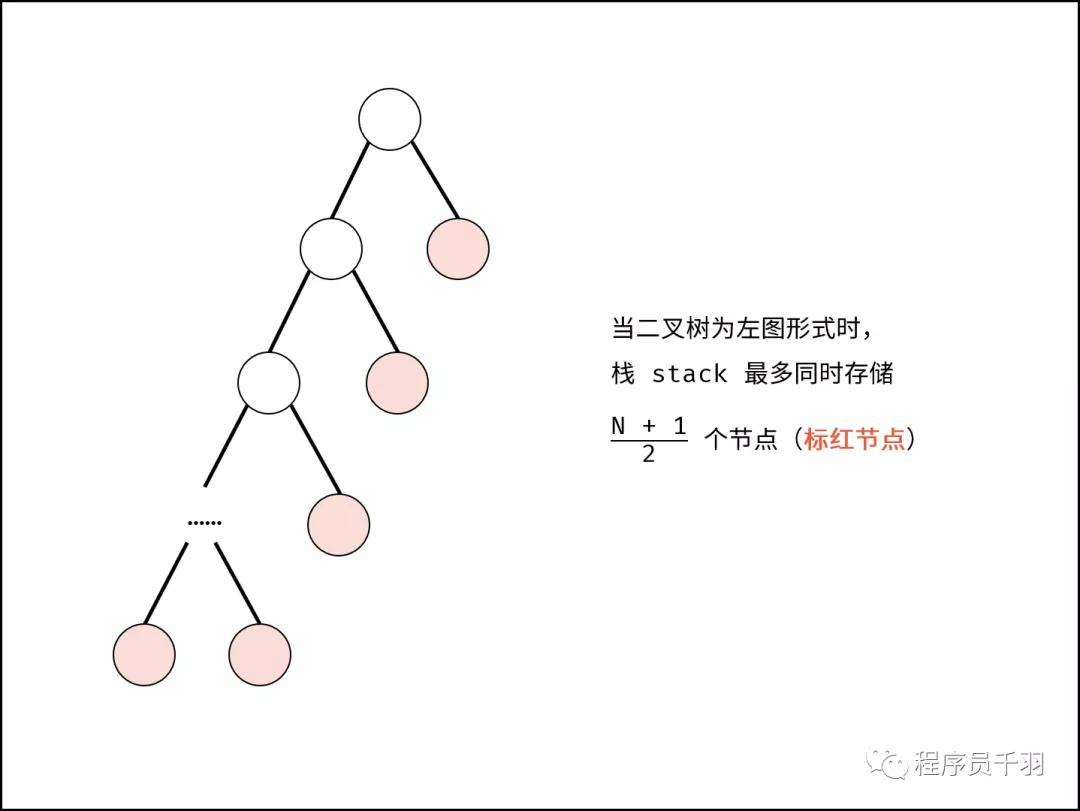
• 空間復雜度O(N) ：如下圖所示,最差情況下，棧stack最多同時存儲N+1/2個節點，占用O(N)額外空間。

package com.nateshao.sword_offer.topic_21_mirrorTree; 
 
import java.util.Stack; 
 
/** 
 * @date Created by 邵桐杰 on 2021/11/24 22:48 
 * @微信公眾號 程序員千羽 
 * @個人網站 www.nateshao.cn 
 * @博客 https://nateshao.gitee.io 
 * @GitHub https://github.com/nateshao 
 * @Gitee https://gitee.com/nateshao 
 * Description: 劍指 Offer 27. 二叉樹的鏡像 
 */ 
public class Solution { 
    /** 
     * 棧 
     * 
     * @param root 
     * @return 
     */ 
    public TreeNode mirrorTree1(TreeNode root) { 
        if (root == null) return null; 
        Stack<TreeNode> stack = new Stack<TreeNode>() {{ 
            add(root); 
        }}; 
        while (!stack.isEmpty()) { 
            TreeNode node = stack.pop(); 
            if (node.left != null) stack.add(node.left); 
            if (node.right != null) stack.add(node.right); 
            TreeNode tmp = node.left; 
            node.left = node.right; 
            node.right = tmp; 
        } 
        return root; 
    } 
    /** 
     * 解法二：迭代，時間復雜度：O(n)，空間復雜度：O(n) 
     * 
     * @param root 
     * @return 
     */ 
    public boolean isSymmetric2(TreeNode root) { 
        Stack<TreeNode> stack = new Stack<>(); 
        stack.push(root); 
        stack.push(root); 
        while (!stack.isEmpty()) { 
            TreeNode t1 = stack.pop(); 
            TreeNode t2 = stack.pop(); 
            if (t1 == null && t2 == null) continue; 
            if (t1 == null || t2 == null) return false; 
            if (t1.val != t2.val) return false; 
 
            stack.push(t1.left); 
            stack.push(t2.right); 
            stack.push(t1.right); 
            stack.push(t2.left); 
        } 
        return true; 
    } 
 
    public class TreeNode { 
        int val; 
        TreeNode left; 
        TreeNode right; 
 
        TreeNode(int x) { 
            val = x; 
        } 
    } 
 
} 

參考鏈接：https://leetcode-cn.com/problems/er-cha-shu-de-jing-xiang-lcof/solution/mian-shi-ti-27-er-cha-shu-de-jing-xiang-di-gui-fu-