樹是編程中的一種最為重要的數(shù)據(jù)結構了，應用范圍很廣。比如說人們常用的操作系統(tǒng)，如Windows和Linux，它們的文件管理系統(tǒng)都是樹型結構的。而這其中二叉樹又是應用最廣的樹，因此也是很多程序員入門時學習的主要數(shù)據(jù)結構。

從外表上來看，二叉樹非常簡單，每個節(jié)點延伸出兩個子節(jié)點，一層一層地延續(xù)下去，像人們的祖譜一樣，非常容易理解。

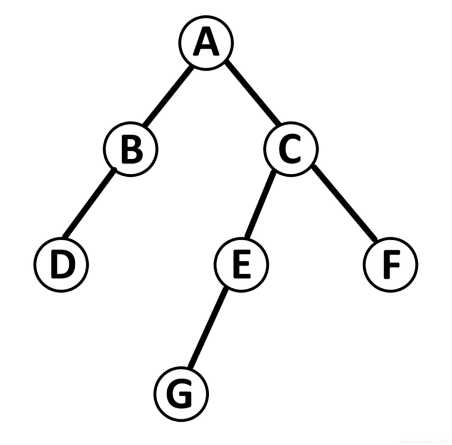
二叉樹相關的編程中，二叉樹的遍歷是最為常見的一種，對于普通人來說，如果想遍歷上圖的二叉樹的話，很多人都會很直白地一層一層讀下去，于是遍歷出來的結果就是ABCDEFG。非常直觀。

但是計算機的計算方式和人們的思維方式是不一樣的，這種層次遍歷對于人來說非常好理解，但是對于計算機來說，并不是很好理解。

所以為了更符合計算機的思考方式，研究人員提出了先序遍歷、中序遍歷、后序遍歷三種算法。這三種算法都是如何遍歷二叉樹的呢？我們來看一下。

一、先序遍歷

先序遍歷(Pre-order)，也叫前序遍歷，按照根左右的順序沿一定路徑經(jīng)過路徑上所有的結點。在二叉樹中，對每個節(jié)點都是，先根后左再右。也就是，根左右。具體實現(xiàn)方法如下：

public static void preOrder(BinTreeNode t) {
    if (null == t ) return;
    System.out.println(t.getData());
    preOrder(t.getlChild());
    preOrder (t.getrChild());
}

對于上圖的二叉樹，遍歷結果為，abdcegf。

二、中序遍歷

中序遍歷，也叫中根遍歷、中序周游。中序遍歷首先遍歷左子樹，然后訪問根結點，最后遍歷右子樹。也就是，左根右。具體實現(xiàn)方法如下：

public static void inOrder(BinTreeNode t) {
    if (null == t ) return;
    inOrder(t.getlChild());
    System.out.println(t.getData());
    inOrder (t.getrChild());
}

對于上圖的二叉樹，遍歷結果為：dbagefc。

三、后序遍歷

后序遍歷（LRD）也叫做后根遍歷、后序周游。后序遍歷首先遍歷左子樹，然后遍歷右子樹，最后訪問要節(jié)點。也就是，左右根。具體實現(xiàn)方法如下：

public static void postOrder(BinTreeNode t) {
    if (null == t ) return;
    postOrder(t.getlChild());
    postOrder (t.getrChild());
    System.out.println(t.getData());
}

對于上圖的二叉樹，遍歷結果為：dbgefca。

可以看到，上面的三種算法中，區(qū)別就是在于打印節(jié)點數(shù)據(jù)（應用節(jié)點數(shù)據(jù)域）的代碼位置不一樣而已。對于計算機來說，使用遞歸算法，非常簡潔明了。

四、層次遍歷

那么更符合人們習慣的層次遍歷，計算機又需要怎樣執(zhí)行呢？我們可以看到，對于計算機而言，最大的問題在于它并不知道哪個節(jié)點屬于哪一層，因此，我們需要使用代碼記錄，每個層次的節(jié)點信息。通常情況下，我們可以使用隊列來實現(xiàn)。代碼如下：

public static void levelOrder(BinTreeNode t) {
    Queue<BinTreeNode> q = new LinkedList<>();
    q.offer(t);
    while (!q.isEmpty()){
        int size = q.size();
        for (int i=0; i<size; i++) {
            BinTreeNode node = q.poll();
            System.out.println(node.getData());
            if (node.getlChild()!= null) q.offer(node.getlChild());
            if (node.getrChild() != null) q.offer(node.getrChild());
        }
    }
}

打印結果為：abcdefg。

我們可以看到，對于人類來講最為簡潔明了的層次算法，對于計算機編程來說，需要的代碼量要大很多。原因在于對于人們來說直觀的約束條件，如哪個節(jié)點在哪一層，對于計算機來說并不直觀。因此，很多時候對于程序員來說，要按照計算機的思維來看問題，這樣寫出的代碼才能更符合計算機的習慣。