譯者 | 朱先忠

審校 | 重樓

簡介

最近，我們團隊推出了一種稱為自動梯度下降（AGD：automatic gradient descent）的優化器，它可以在不使用超參數的情況下訓練ImageNet數據集。基于這一優化器算法，可以消除在模型訓練時對昂貴且耗時的學習速率調整、學習速率衰減調度器等選項的需求。您可以在鏈接處找到我們發表的有關此算法的論文。

我與Jeremy Bernstein、Kevin Huang、Navid Azizan和Yisong Yue一起參與了這個項目。您可以參閱Jeremy先生的GitHub代碼庫以獲得一個干凈的Pytorch實現，也可以參閱我的GitHub代碼庫以獲得具有更多功能的實驗版本。下面的圖1總結了我們提出的AGD算法與Adam和SGD兩種優化算法之間的對比情況。

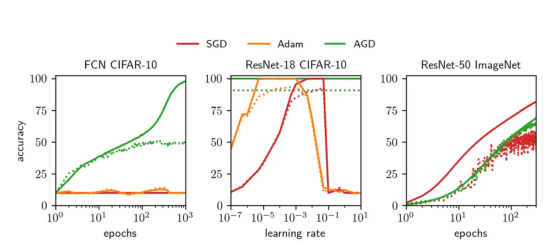
圖1：實線顯示訓練精度，虛線顯示測試精度

其中，左圖展示的是與我們的方法相反的具有默認超參數的Adam和SGD算法在CIFAR-10數據集上的深度全連接網絡（FCN）上不理想的表現。中間圖展示的是Adam和SGD算法的學習率網格搜索對比情況。我們所開發的優化器的性能與經過充分調參后的Adam和SGD性能差不多。右圖展示了我們所開發的AGD算法將ImageNet數據集訓練到相當高的測試精度。

動機

任何訓練過深度神經網絡的人都可能有過不得不調整模型的學習速率的經歷。這樣做的目的無處乎：（1）確保訓練的最大效率；（2）找到正確的學習率可以顯著提高整體模型的泛化應用能力。當然，這個過程也會伴隨著開發人員的巨大代價的付出。

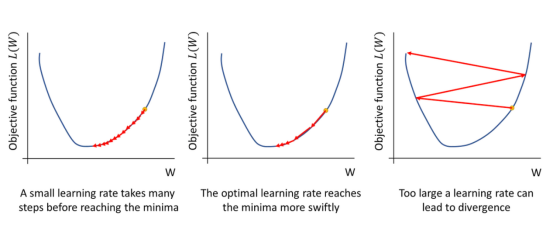
圖2：為什么學習率對模型優化非常重要

為了最大限度地提高收斂速度，你總會想盡可能找到最佳學習率：這是很大的一個值！而且，目標函數中的非線性項可能會把你折磨得“死去活來”。

然而，對于SGD算法來說，最佳學習率在很大程度上取決于正在訓練的體系結構。找到這個值通常需要一個代價高昂的網格搜索程序，需要涵蓋許多數量級內容。此外，還需要選擇和調整其他超參數，如動量和學習率衰減調度器。

為此，我們提出了一種稱為自動梯度下降（AGD）的優化器，它不需要使用學習率就可以訓練大范圍的架構和數據集，可以在ImageNet數據集上從基礎模型一直擴展訓練到ResNet-50這樣的復雜模型。這種算法消除了對任何超參數調整的需要（因為此算法不需要分析有效學習率和學習率衰減值），從而節省了計算成本，并大大加快了模型訓練的過程。

為什么我們需要超參數呢？

究其原因，一個深度學習系統往往都是由許多相互關聯的組件組成：架構、數據、損失函數和梯度等。這些組件的交互方式都是圍繞著一種結構進行的；但是，到目前為止，還沒有人確切地弄清楚這個結構。所以，我們需要進行大量的調整工作（例如學習率、初始化、調度器等），以確保快速收斂，并避免過度擬合。

然而，盡管完美地描述這些相互作用可以消除優化過程中的所有自由度；但是，目前這些自由度都是通過手動超參數調整來實現的。二階方法中目前使用Hessian矩陣來表征目標對權重擾動的敏感性，并以這種方式去除自由度——然而，這種方法可能計算密集，因此對于大型模型來說并不實用。

我們團隊通過分析這些相互作用的特征，最終找到了AGD優化方法：

1. 對于給定的數據和架構，我們根據權重的變化來約束神經網絡輸出的變化。
2. 我們將目標的變化（一次批運算中所有輸入的總損失）與神經網絡輸出的變化聯系起來。
3. 我們將這些結果結合在一種所謂的多數最小化方法（majorise-minimise approach）中。我們對目標進行多數化——也就是說，我們推導出與目標相切的目標的上界。然后我們可以將這個上限降到最低，因為我們知道這會讓我們的算法加快收斂。如圖3所示，紅色曲線表示目標函數的多數化，藍色曲線表示目標函數。

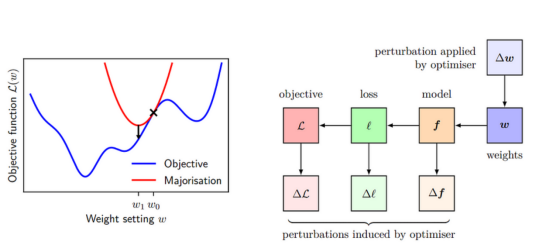
圖3：左側面板顯示了多數最小化背后的基本思想

最小化目標函數（藍色）是通過最小化一系列上限或多數（紅色）來實現的。右側面板顯示了權重的變化如何導致函數的變化，進而導致單個數據點的損失的變化，從而導致目標的變化。我們用?W來約束?L，并用它來構建我們的多數化。

基于Pytorch框架的AGD算法實現

在本節中，我們將介紹我們所開發的AGD優化算法的所有關鍵部分基于Pytorch框架的實現代碼。相應的草圖推導可參考文后的附錄A。

參數操作

我們所使用的參數化與傳統PyTorch默認值略有不同。AGD算法可以在不借助參數化支持的情況下即可完成；不過，使用參數化可以簡化分析過程。對于完全連接的層l，我們使用正交初始化，并進行適當的縮放以便使奇異值具有大小：sqrt((l的輸入維度)/(l的輸出維度))。

import math
import torch
from torch.nn.init import orthogonal_

def singular_value(p):
 sv = math.sqrt(p.shape[0] / p.shape[1])
 if p.dim() == 4:
 sv /= math.sqrt(p.shape[2] * p.shape[3])
 return sv

class AGD:
 @torch.no_grad()
 def __init__(self, net, gain=1.0):

 self.net = net
 self.depth = len(list(net.parameters()))
 self.gain = gain #用于加速訓練的可選用的超參數——在后面的任何實驗中并不使用

 for p in net.parameters():
 if p.dim() == 1: raise Exception("Biases are not supported.")
 if p.dim() == 2: orthogonal_(p)
 if p.dim() == 4:
 for kx in range(p.shape[2]):
 for ky in range(p.shape[3]):
 orthogonal_(p[:,:,kx,ky])
 p *= singular_value(p)

在此，我們之所以使用這種規范化，是因為它具有PyTorch默認參數化所沒有的優秀特征，包括寬度穩定性、對激活函數中的抗爆炸式增長能力以及促進特征學習。這與Greg Yang和Edward Hu二人開發的muP庫相似。

更新操作

這一步可以分成兩個單獨的部分。第一個是計算eta（η），即“自動學習率”，它實現對所有層的更新進行縮放。注意，Eta對梯度范數有對數依賴性——當梯度很小時，Eta近似為線性（就像標準優化器一樣）；但是，當它們非常大時，對數會自動執行一種梯度修剪。

@torch.no_grad()
 def step(self):
 G = 0
 for p in self.net.parameters():
 G += singular_value(p) * p.grad.norm(dim=(0,1)).sum()
 G /= self.depth
 eta = math.log(0.5 * (1 + math.sqrt(1 + 4*G)))

 for p in self.net.parameters():
 factor = singular_value(p) / p.grad.norm(dim=(0,1), keepdim=True)
 p -= self.gain * eta / self.depth * factor * p.grad

 return log

使用eta乘以層的權重范數、乘以歸一化梯度并除以深度來更新每個層。除以深度實現了按深度縮放。有趣的是，分析中沒有使用梯度歸一化，因為像Adam這樣的其他優化器也啟發式地引入了類似的想法。

實驗

進行這些實驗的目標是為了測試AGD優化算法的能力：（1）在廣泛的體系結構和數據集上的收斂性能；以及（2）實現與調參后的Adam和SGD算法相當的測試精度。

接下來的圖4顯示了從完全連接網絡（FCN）到ResNet-50網絡的四種架構在從CIFAR-10到ImageNet的數據集上的學習曲線。我們將實線所示的AGD優化器與虛線所示的標準優化器進行比較（SGD基于ImageNet數據集，調優后的Adam對應于其他三種情況）。最上面一行顯示了訓練目標（損失）和自動學習率η。最下面一行顯示了訓練和測試的準確性。圖5展示了在8層FCN上進行比較的AGD、調優后的Adam與調優后的SGD。我們看到所有三種算法的性能非常相似，達到了幾乎相同的測試精度。

圖6顯示，AGD在較寬的深度（2至32）和寬度（64至2048）范圍內訓練FCN。圖7顯示了AGD對批次大小（從32到4096）和4層FCN的依賴性。無論批量大小，它似乎都會收斂到一個很好的最優值！

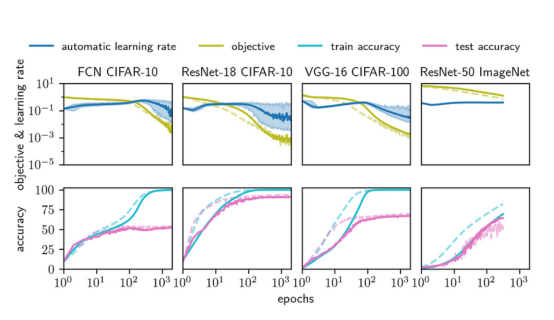
圖4——四種架構上的AGD與Adam算法比較：CIFAR-10上的16層深的FCN、CIFAR-10的ResNet-18、CIFAR-100上的VGG-16和ImageNet-1k上的ResNet-50。AGD與超參數調優后的Adam保持合理的速度（這需要網格搜索幾個數量級）！

這些實線表示AGD，虛線表示Adam（除了ImageNet，我們使用SGD）。最上面一行顯示了訓練目標（即損失）和訓練期間自動學習率η的值。最下面一行顯示了訓練和測試的準確性。

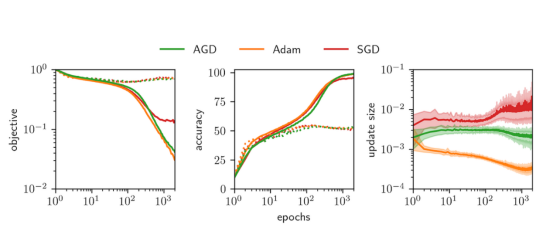
圖5：具有均方誤差損失的深度為8的FCN網絡上的AGD、Adam與SGD算法比較

值得注意的是，Adam和SGD都調整了它們的學習率。在左邊圖形中，我們繪制了訓練和測試目標函數（即損失）。中間圖形顯示了訓練和測試的準確性。右邊圖形顯示了每個訓練周期期間權重的平均值、最小值和最大值變化。

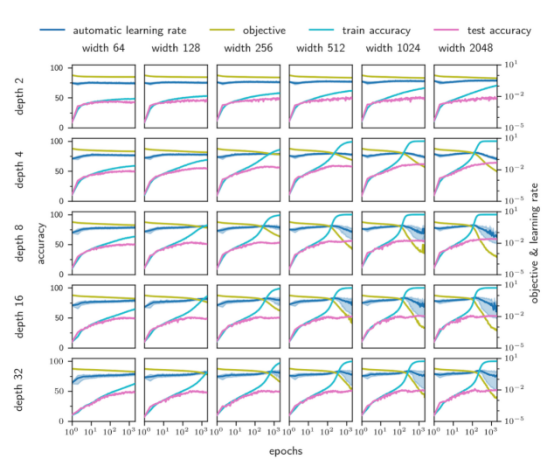
圖6：AGD算法在很大的深度和寬度范圍內能夠自如地收斂。不過，較小的架構往往缺乏實現低損耗的能力，但AGD仍可以訓練它們！

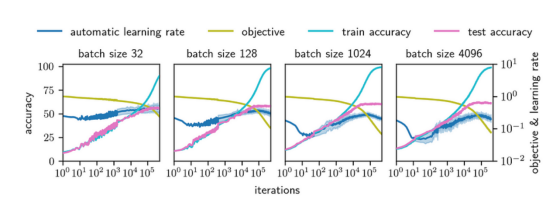
圖7：為了檢查AGD算法不僅適用于批量大小128，這里還提供了一個深度為4的FCN模型的批量大小選擇

結論

總的來說，本文實現了一個“架構感知”類型優化器：自動梯度下降（AGD），它能夠在指定的批量范圍大小下訓練成功從CIFAR-10數據集上的FCN等小型模型系統直到大型數據集ImageNet上的ResNet-50等大型模型系統，而無需手動進行超參數調整。

雖然使用AGD并沒有從機器學習中完全刪除所有的超參數，但剩下的超參數——批量大小和體系結構——通常能夠實現均衡時間/計算方面的預算代價。

盡管如此，仍然有許多工作要做。例如，我們沒有明確考慮由于批次大小而引入梯度的隨機性。此外，我們也沒有研究像權重衰減這樣的規則化。雖然我們在增加對仿射參數（在批處理范數層中）和偏差項的支持方面做了一些工作，但我們還沒有對其進行廣泛的測試，也沒有像本文引用的其他結果那樣從理論上證明它是合理的。

也許最重要的是，我們仍然需要進行轉換器（Transformer）所需的分析，并在NLP任務中測試AGD。在OpenWebText2上對GPT-2進行的初步實驗表明，AGD在這種情況下也非常有效！

最后，如果你想嘗試使用AGD算法的話，請查看Jeremy的GitHub代碼以獲得一個干凈的版本，或者查看我的GitHub以獲得支持偏置和仿射參數的開發版本！我們希望你會覺得這個算法有用。

附錄A

最后，我們將在這里簡要介紹一下我們論文證明過程中的一些重要步驟。這是為那些想看看此算法的主要思想是如何結合在一起的人設計的，而不需要經過我們論文中的完整證明。

其中，方程（1）明確規定了如何將數據集S上的總體目標分解為各個數據點。L表示損失，x表示輸入，y表示目標，w表示權重。方程（2）顯示了目標線性化誤差的分解——在權重Δw發生變化的情況下，高階項對損失ΔL（w）變化的貢獻。目標的線性化誤差很重要，因為它等于在權重w-bounding下擴展的損失中的高階項的貢獻，這將告訴我們在高階項變得重要之前我們可以移動多遠，并確保我們正在采取合理大小的步長實現收斂。

方程（2）中的RHS上的第一項是兩個高維向量、模型的線性化誤差和損耗相對于f（x）的導數之間的內積。由于沒有明確的理由說明為什么這兩個向量應該對齊，我們假設它們的內積為零。

將L（W+ΔW）加到方程（2）的每一側，并注意到損失的線性化誤差恰好是布雷格曼散度（Bregman Divergence），我們可以進一步簡化符號表示：

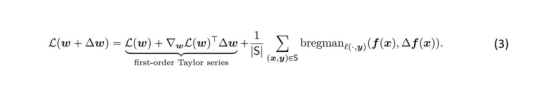
Bregman散度是兩點之間距離的度量（在這種情況下，是神經網絡兩個不同參數選擇的輸出），用嚴格凸函數定義——在這種情況中，即損失函數。

對于均方誤差損失來說，計算Bregman散度實際上是非常簡單的。并且，我們容易得出如下表達：

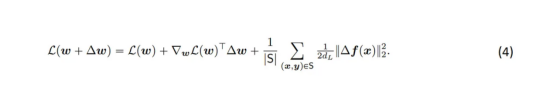
其中，d是網絡的輸出維度。我們現在可以斷言存在以下縮放表達式。盡管所有這些都有點武斷；但是，采用這種形式會使問題分析變得更加簡單。

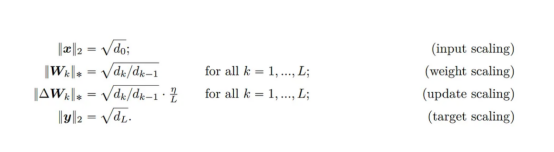
我們對網絡輸出的大小使用以下兩個界限。其中，方程（5）限制了網絡輸出的大小，并且僅將（輸入縮放）和（權重縮放）應用于完全連接的網絡。方程（6）限制了f（x）的最大變化與權重W的變化。（6）中的第二個不等式在大深度下最緊，但在任何深度下都成立。

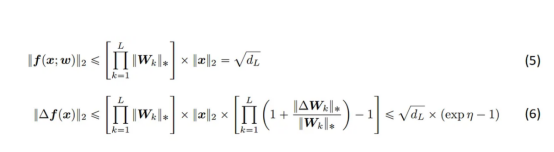
現在，我們將方程（6）代入方程（4），并將所有項顯式展開，得到方程（7）。

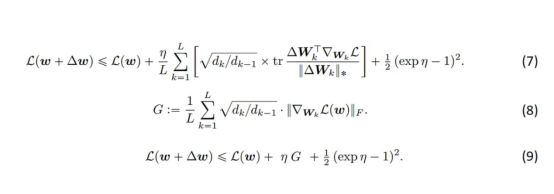
在關于梯度條件的附加假設下，我們可以用方程（8）中定義的G代替方程（7）中的和，這在本文中進行了詳細討論。最后，我們得到方程（9）——這是多數化——圖3中的紅線。我們通過對η進行微分來最小化多數化，并在exp（η）中求解由此產生的二次方，保留正解。于是，我們有了以下新的表達形式：

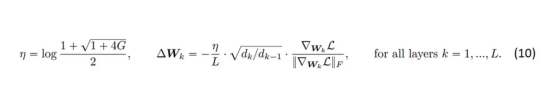
至此，就完成了我們對自動梯度下降的推導介紹。如果您有任何意見、問題或其他類型的反饋，請告訴我們。

最后需要說明的是，本博客中的所有圖片都是由我們論文的作者制作的，圖2受鏈接https://www.jeremyjordan.me/nn-learning-rate/文章中的圖啟發而制作的。

譯者介紹

朱先忠，51CTO社區編輯，51CTO專家博客、講師，濰坊一所高校計算機教師，自由編程界老兵一枚。

原文標題：Train ImageNet without Hyperparameters with Automatic Gradient Descent，作者：Chris Mingard