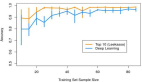
Chinchilla之死:只要訓(xùn)練足夠長(zhǎng)時(shí)間,小模型也能超過大模型
2022 年 3 月,DeepMind 一篇論文《Training Compute-Optimal Large Language Models》通過構(gòu)建的 Chinchilla 模型得出了一個(gè)結(jié)論:大模型存在訓(xùn)練不足的缺陷,模型大小和訓(xùn)練 token 的數(shù)量應(yīng)該以相等的比例擴(kuò)展。也就是說(shuō)模型越大,所使用的訓(xùn)練 token 也應(yīng)該越多。

但事實(shí)可能并非如此,近日,博主 Thaddée Yann TYL 寫了一篇題為《Chinchilla 之死》的文章,其中分析解讀了 OpenAI 與 DeepMind 幾篇論文中的細(xì)節(jié),得到了一個(gè)出人意料的結(jié)論:如果有充足的計(jì)算資源和數(shù)據(jù),訓(xùn)練足夠長(zhǎng)時(shí)間,小模型的表現(xiàn)也可以超越大模型。
多算勝,少算不勝。——《孫子兵法》
為了避免將算力浪費(fèi)于緩慢的收斂過程中,進(jìn)行外推是非常重要的。畢竟,如果你不得不步行去珠穆朗瑪峰,你不會(huì)只靠眼睛辨別方向,而是會(huì)使用 GPS。
但有時(shí)候,你又不得不把視線從 GPS 上移開,看看道路。有些東西是無(wú)法通過簡(jiǎn)單的公式推斷出來(lái)的。對(duì)十九世紀(jì)的物理學(xué)家來(lái)說(shuō),紫外災(zāi)變( Ultraviolet catastrophe)便是如此;而現(xiàn)在,LLM 亦是如此。我們估計(jì)在中心位置附近有效的東西可能在遠(yuǎn)處會(huì)出現(xiàn)巨大的偏差……

《我的世界》的邊境之地(far lands),這是突然扭曲并與自身重疊的懸崖之地。
Chinchilla 到底是什么?
更小的模型執(zhí)行的乘法更少,因而訓(xùn)練得也更快。但是,按照理論,更小的模型最終會(huì)觸及自身知識(shí)容量的極限,并且學(xué)習(xí)速度會(huì)變慢;而有更大知識(shí)容量的大型模型在經(jīng)過給定的訓(xùn)練時(shí)間后會(huì)超過小模型,取得更好的性能表現(xiàn)。
在評(píng)估如何在訓(xùn)練期間獲得最佳性價(jià)比時(shí),OpenAI 和 DeepMind 都會(huì)試圖繪制帕累托邊界(Pareto frontier)。雖然他們沒有明確說(shuō)明他們使用了該理論來(lái)繪制,但 OpenAI 曾說(shuō)過的一句話暗示存在這個(gè)隱藏假設(shè):
我們預(yù)計(jì)更大模型的表現(xiàn)應(yīng)當(dāng)總是優(yōu)于更小的模型…… 大小固定的模型的能力是有限的。
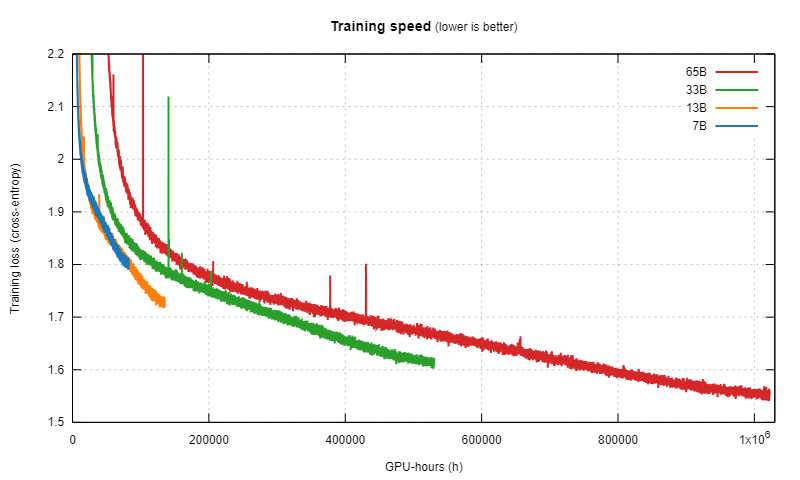
這一假設(shè)是他們計(jì)算帕累托邊界的基石。在 Chinchilla 研究中,圖 2 展示了不同大小的模型經(jīng)過大量訓(xùn)練時(shí)的訓(xùn)練損失變化情況。初看之下,這些曲線與理論相符:更小的模型一開始的損失更低(表現(xiàn)更好),但損失降低的速度最終變慢并被更大模型的曲線超越。
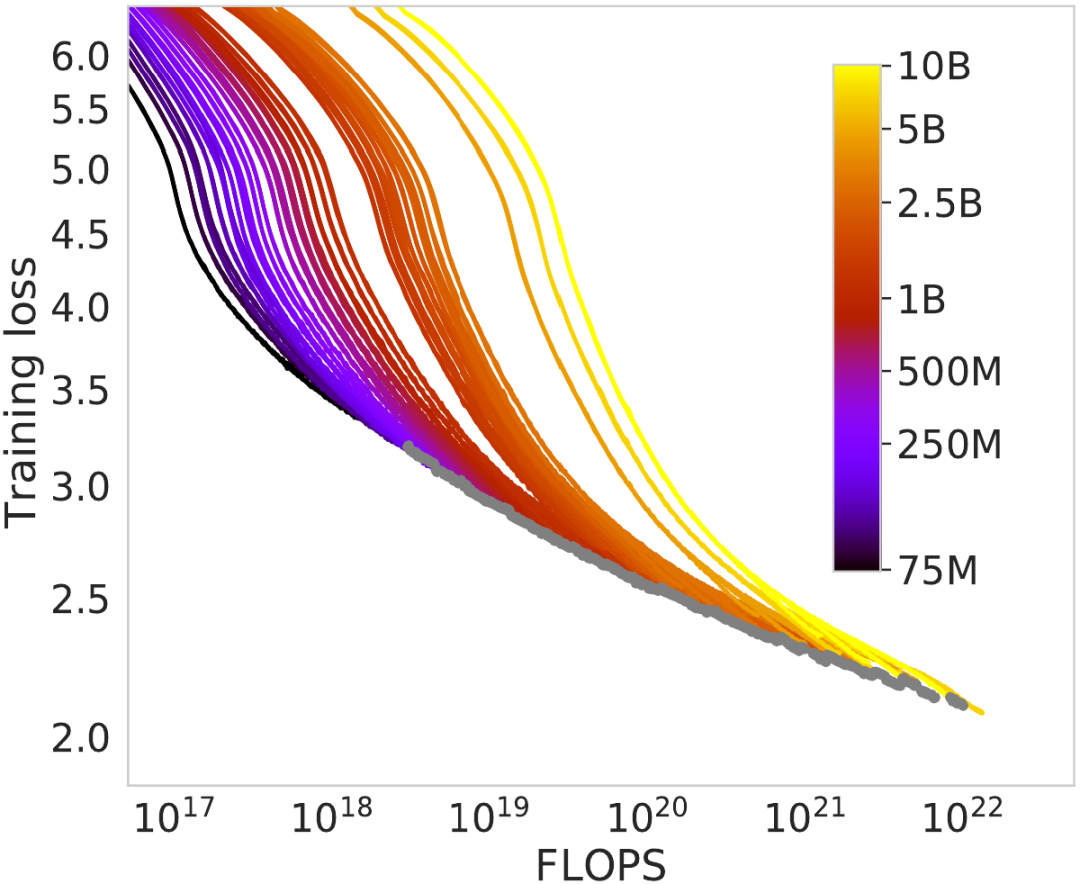
比較許多不同模型大小的損失曲線的 Chinchilla 圖
在這幅圖中,每當(dāng)更小的模型輸給一個(gè)更大的模型時(shí),他們就會(huì)標(biāo)記一個(gè)灰點(diǎn)。這些點(diǎn)連成的灰線便是帕累托邊界,這是他們計(jì)算縮放定律(scaling laws)的方式。
這一假設(shè)有個(gè)問題:我們不知道如果讓更小的模型訓(xùn)練更長(zhǎng)時(shí)間會(huì)發(fā)生什么,因?yàn)樗麄冊(cè)谛∧P捅怀綍r(shí)就不再繼續(xù)訓(xùn)練它們了。
接下來(lái)在看看 Llama 論文。
Chinchilla 會(huì)有 Llama 的視野嗎?
今年初,Meta 訓(xùn)練了四個(gè)不同大小的模型。不同于其它研究,其中每個(gè)模型都被訓(xùn)練了非常長(zhǎng)時(shí)間,較小的模型也一樣。
他們公布了所得到的訓(xùn)練曲線:
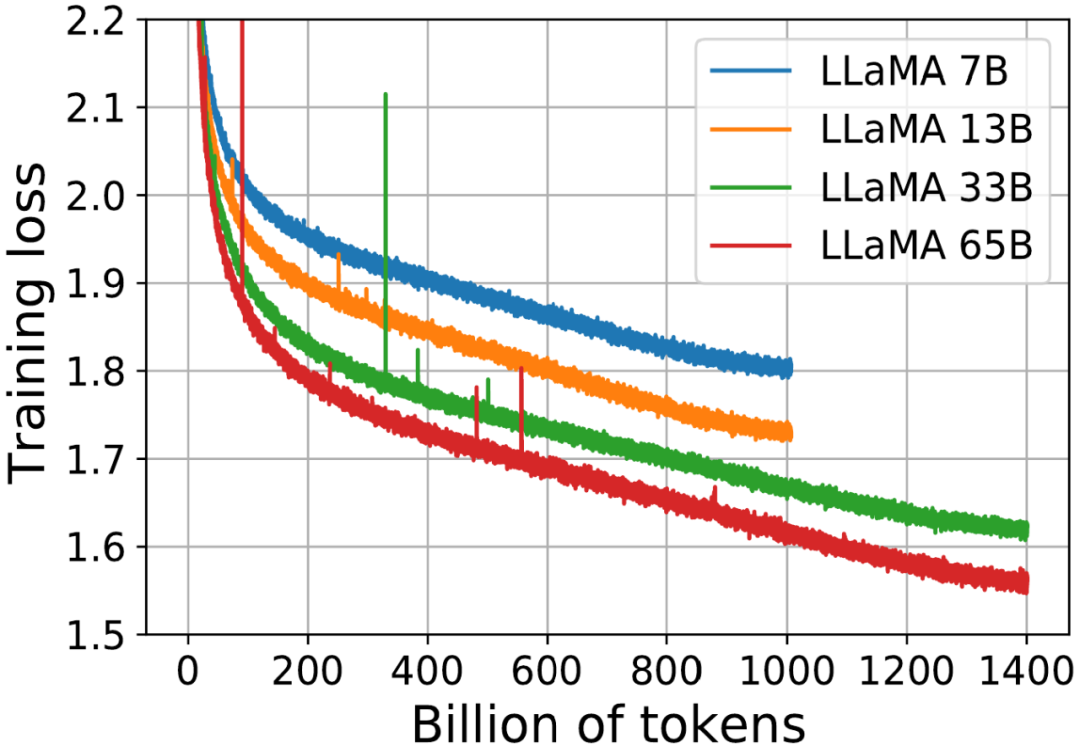
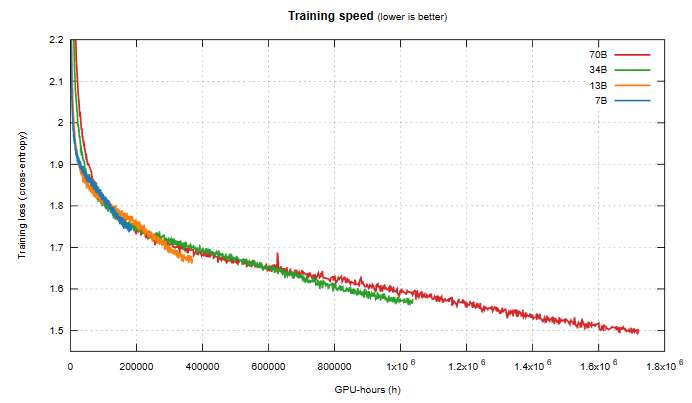
四個(gè)不同大小的 Llama 模型的訓(xùn)練損失曲線
- 每條曲線首先按照冪律大幅下降。
- 然后損失開始近乎線性地下降(對(duì)應(yīng)于一個(gè)相當(dāng)恒定的知識(shí)獲取率)。
- 在這條曲線的最右端,直線趨勢(shì)被稍微打破,因?yàn)樗鼈兩晕⒆兏骄徚艘恍?/li>
首先,對(duì)于曲線末端的變平情況,這里解釋一下人們可能有的一個(gè)微妙的誤解。這些模型都是通過梯度下降訓(xùn)練的并且使用了可變的學(xué)習(xí)率(大致來(lái)說(shuō),這個(gè)超參數(shù)定義了每次朝梯度方向前進(jìn)的程度)。為了獲得優(yōu)良的訓(xùn)練效果,學(xué)習(xí)率必須不斷降低,這樣模型才能檢測(cè)到源材料中更細(xì)微的模式。他們用于降低學(xué)習(xí)率的公式是最常用的余弦調(diào)度(cosine schedule)。
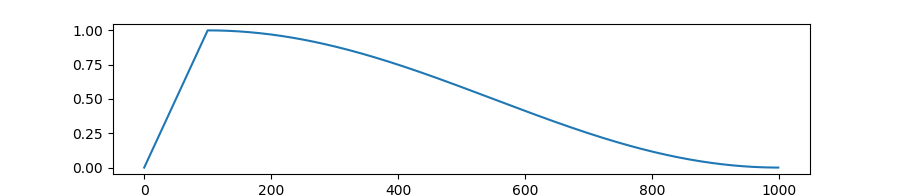
在余弦調(diào)度下,學(xué)習(xí)率與訓(xùn)練步數(shù)的函數(shù)關(guān)系:學(xué)習(xí)率首先線性增長(zhǎng),然后下降且下降速度變快,之后到達(dá)中途一個(gè)轉(zhuǎn)折點(diǎn),下降速度再減慢。
從這張圖中可以看到,在訓(xùn)練結(jié)束時(shí),余弦調(diào)度會(huì)停止降低學(xué)習(xí)率,此時(shí)已經(jīng)得到一個(gè)很好的近乎線性的訓(xùn)練損失曲線。學(xué)習(xí)速度減慢就是這種做法造成的。模型并不一定不再具有以同樣近乎線性的速率學(xué)習(xí)的能力!事實(shí)上,如果我們能為其提供更多文本,我們就能延長(zhǎng)其余弦調(diào)度,這樣其學(xué)習(xí)率就會(huì)繼續(xù)以同樣速率下降。
模型的適應(yīng)度圖景并不取決于我們供給它訓(xùn)練的數(shù)據(jù)量;所以學(xué)習(xí)率下降趨勢(shì)的改變是沒有道理的。
不過這并非本文的重點(diǎn)。
訓(xùn)練損失曲線可能在另一方向上也存在誤導(dǎo)性。當(dāng)然,它們訓(xùn)練使用的數(shù)據(jù)是一樣的,但它們處理這些數(shù)據(jù)的速度不同。我們想知道的并不是模型的樣本效率如何(在這方面,更大的模型顯然可以從其所見數(shù)據(jù)中學(xué)到更多)。讓我們想象一場(chǎng)比賽:所有這些模型同時(shí)開始起步,我們想知道哪個(gè)模型首先沖過終點(diǎn)線。換句話說(shuō),當(dāng)在訓(xùn)練時(shí)間投入固定量的算力時(shí),哪個(gè)模型能在那段時(shí)間內(nèi)學(xué)到更多?
幸好我們可以把這些損失曲線與 Meta 提供的另一些數(shù)據(jù)組合起來(lái)看:每個(gè)模型訓(xùn)練所用的時(shí)間。
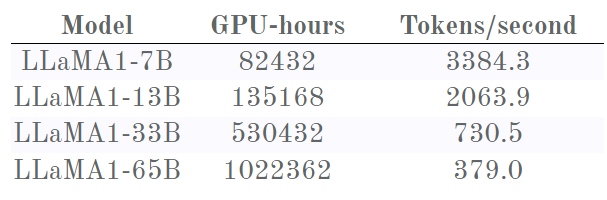
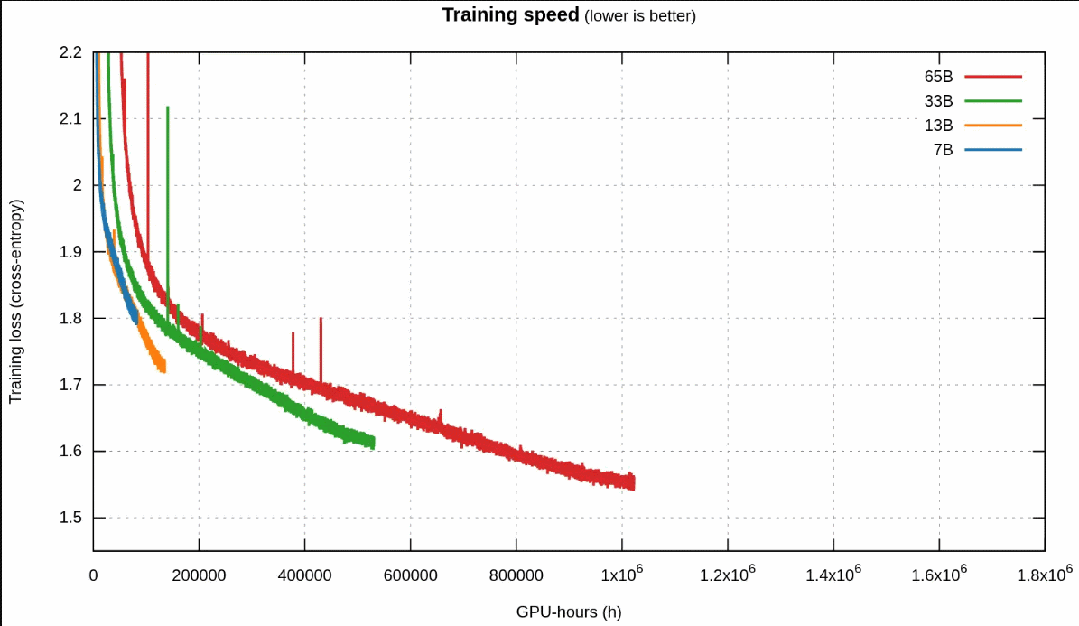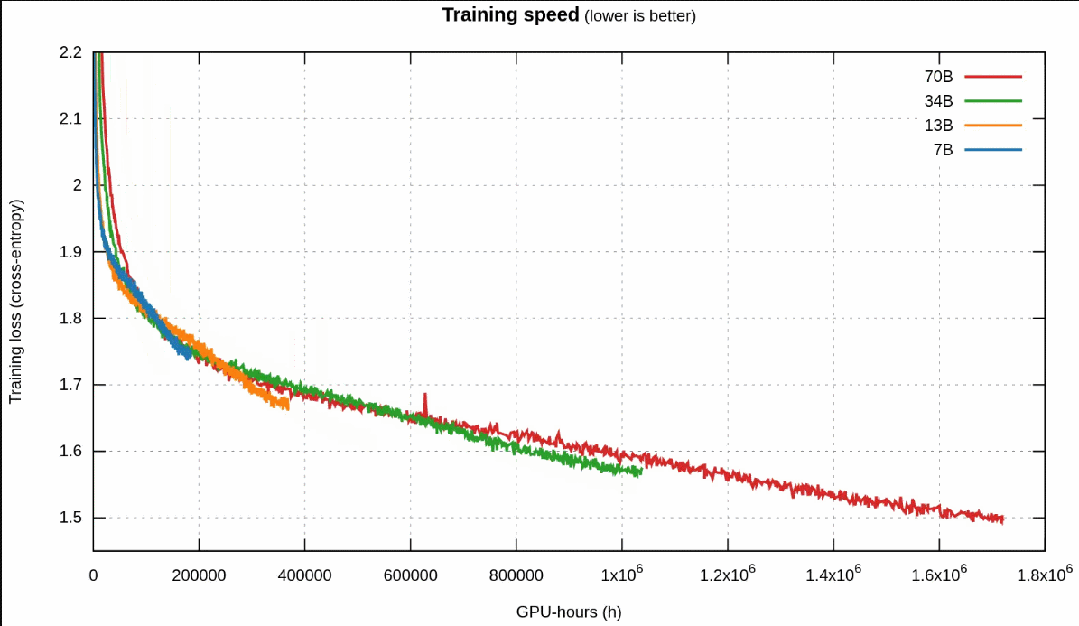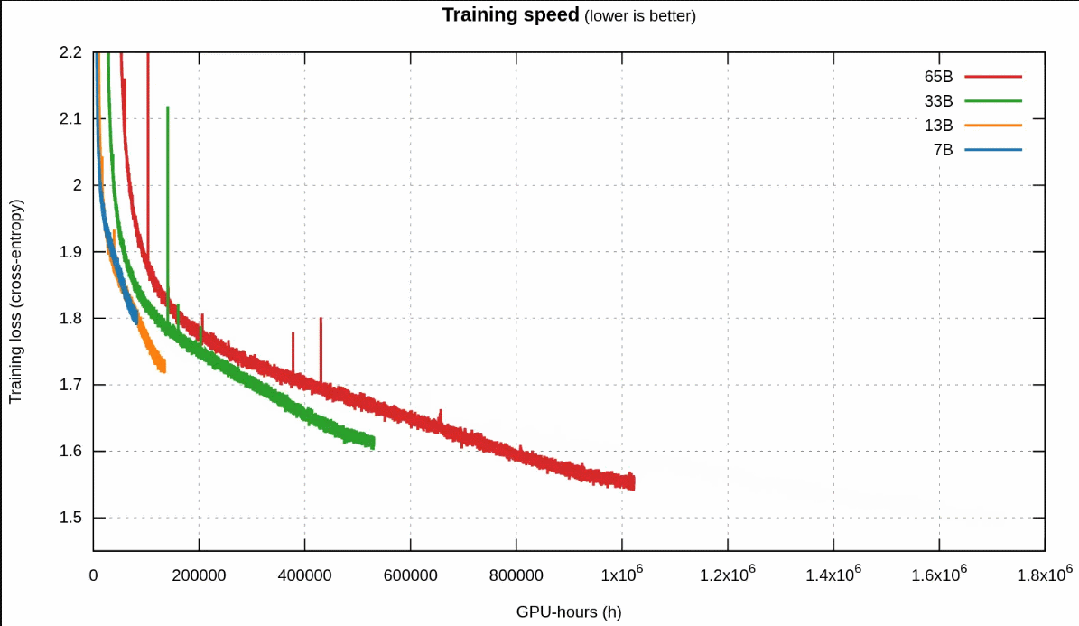
先來(lái)談?wù)勆厦嫖覀兛催^的那張 Chinchilla 圖,其僅占這張圖左側(cè)的一小部分。在這一小部分,可以看到 Chinchilla 記錄的相同行為。以 7B 版本為例:其損失的下降速度一開始比更大的模型快得多,然后減慢;之后 13B 版本模型超過了它,率先到達(dá) 1.9。
然后,抵達(dá)邊境之地,意外的轉(zhuǎn)折出現(xiàn)了:7B 版本進(jìn)入了近乎線性的疆域,損失穩(wěn)步下降,看起來(lái)似乎走上了反超 13B 版本之路?如果能訓(xùn)練 7B 版本更長(zhǎng)時(shí)間,說(shuō)不好會(huì)發(fā)生什么。
但是,13B 和 33B 版本之間似乎也有類似的現(xiàn)象,其中 13B 版本起初的 Chinchilla 減慢也使其呈現(xiàn)出近乎線性的趨勢(shì),這時(shí)候 13B 版本的損失下降速度似乎很快!33B 其實(shí)勝之不武,因?yàn)樗?13B 版本時(shí)已經(jīng)用去了超過兩倍的計(jì)算時(shí)間。
33B 和 65B 版本之間也有同樣的先減速再加速的現(xiàn)象,以至于 33B 實(shí)際上從未被 65B 超越。這幅圖的內(nèi)容擊破了 OpenAI 和 Chinchilla 的假設(shè):更大的模型并未取得勝利(至少說(shuō)還沒有)。他們檢測(cè)到的這種減速實(shí)際上并不是由于達(dá)到了某個(gè)能力極限!
盡管如此,7B 模型的線還是有點(diǎn)不盡如人意。如果 Meta 能訓(xùn)練更長(zhǎng)時(shí)間就好了……
不賣關(guān)子了:他們訓(xùn)練了!他們發(fā)布了 Llama 2!
是時(shí)候證實(shí)我們的懷疑了
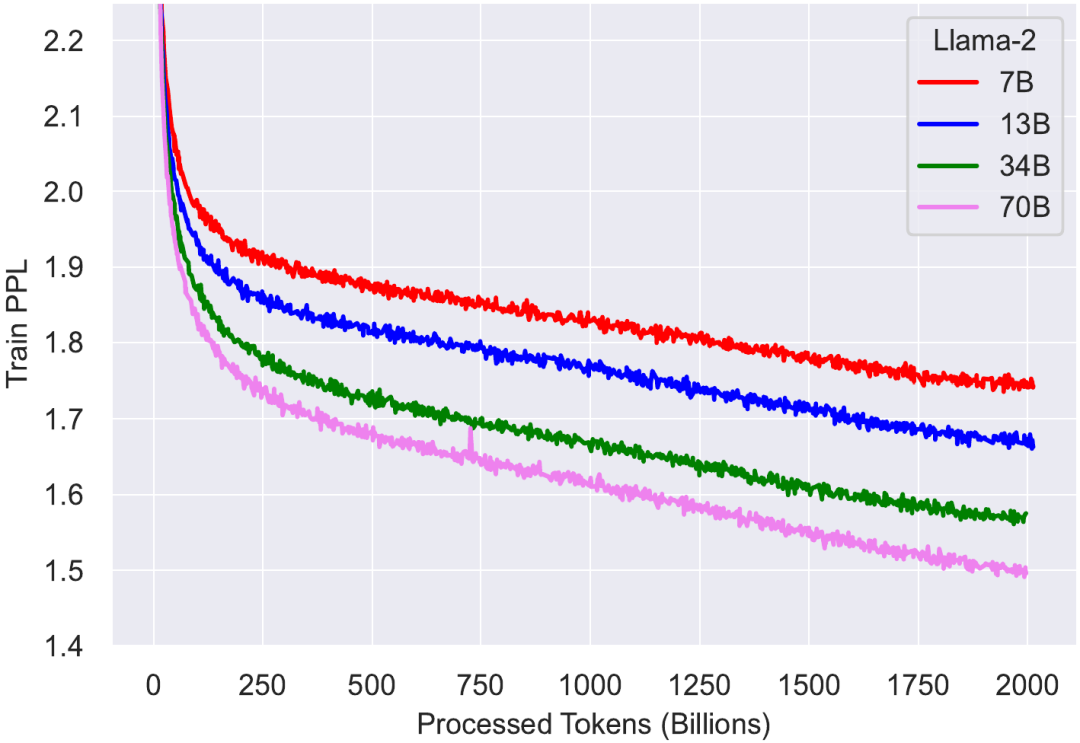
四個(gè)不同大小的 Llama 2 模型的訓(xùn)練損失曲線
同樣,可以得到訓(xùn)練時(shí)間:
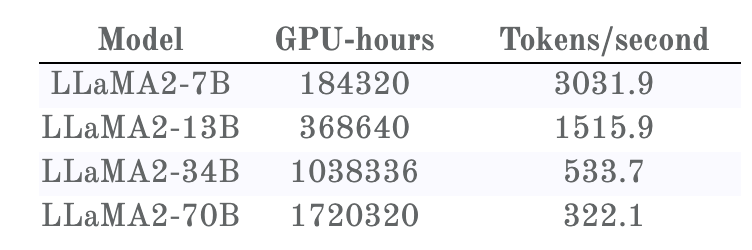
Llama 2 訓(xùn)練損失與所耗費(fèi)的 GPU 時(shí)間
一眼便能看出,這里的訓(xùn)練損失曲線與 Llama 1 的不一樣,即便這些基礎(chǔ)模型是一樣的。事實(shí)證明, Llama 2 的訓(xùn)練使用了雙倍上下文大小和更長(zhǎng)的余弦調(diào)度 —— 不幸的是,這會(huì)對(duì)所有模型大小產(chǎn)生負(fù)面影響。但是,更小的模型受到的影響比更大的模型更嚴(yán)重。由此造成的結(jié)果是:在 Llama 1 的訓(xùn)練時(shí)間,33B 模型總是優(yōu)于 65B 模型;而在 Llama 2 的訓(xùn)練時(shí)間,34B 模型則在重新超過 70B 模型之前要略遜一籌。
更重要的是,對(duì)訓(xùn)練速度的比較強(qiáng)烈地佐證了之前對(duì) Llama 1 的猜想:
- 一開始時(shí),更小的模型快于更大的模型。
- 然后,更小的模型速度變慢,并被更大的模型超越(按照 Chinchilla)。
- 但再然后,模型進(jìn)入近乎線性的區(qū)域,這時(shí)候更小的模型能更快地下降,獲取更優(yōu)的知識(shí),它們?cè)俅纬礁蟮哪P汀?/li>
這就帶來(lái)了一個(gè)有關(guān)訓(xùn)練方法的結(jié)論:與普遍的看法相反,更大的模型會(huì)產(chǎn)生更差的結(jié)果。如果你必須選擇一個(gè)參數(shù)大小和數(shù)據(jù)集,你可能最好選擇 7B 模型,然后在數(shù)萬(wàn)億 token 上訓(xùn)練 7 epoch。
請(qǐng)看看 7B 模型近乎線性的區(qū)域,然后將其模式外推給 70B 模型,看看 70B 模型訓(xùn)練停止時(shí)的情況:如果將 70B 模型的訓(xùn)練資源花在 7B 模型上,可能會(huì)達(dá)到更低的困惑度!
從 Llama 2 的曲線還能看到另一點(diǎn):Llama 1 曲線末端的學(xué)習(xí)減速實(shí)際上是余弦調(diào)度造成的。在 Llama 2 的訓(xùn)練中,在對(duì)應(yīng)于 1 萬(wàn)億 token 讀取數(shù)的位置,就完全沒有這種減速。
事實(shí)上,原因可能是這樣的:在同一位置, Llama 2 7B 模型的質(zhì)量低于 Llama 1 7B 模型,可能是因?yàn)槠溆嘞艺{(diào)度被拉長(zhǎng)了!
現(xiàn)在我們回到那篇 Chinchilla 論文來(lái)論證這一點(diǎn)。在該論文的附錄 A 的圖 A1 中,他們給出了一個(gè)不同余弦調(diào)度參數(shù)的消融實(shí)驗(yàn),換句話說(shuō)就是對(duì)學(xué)習(xí)率曲線使用不同的延展方式。
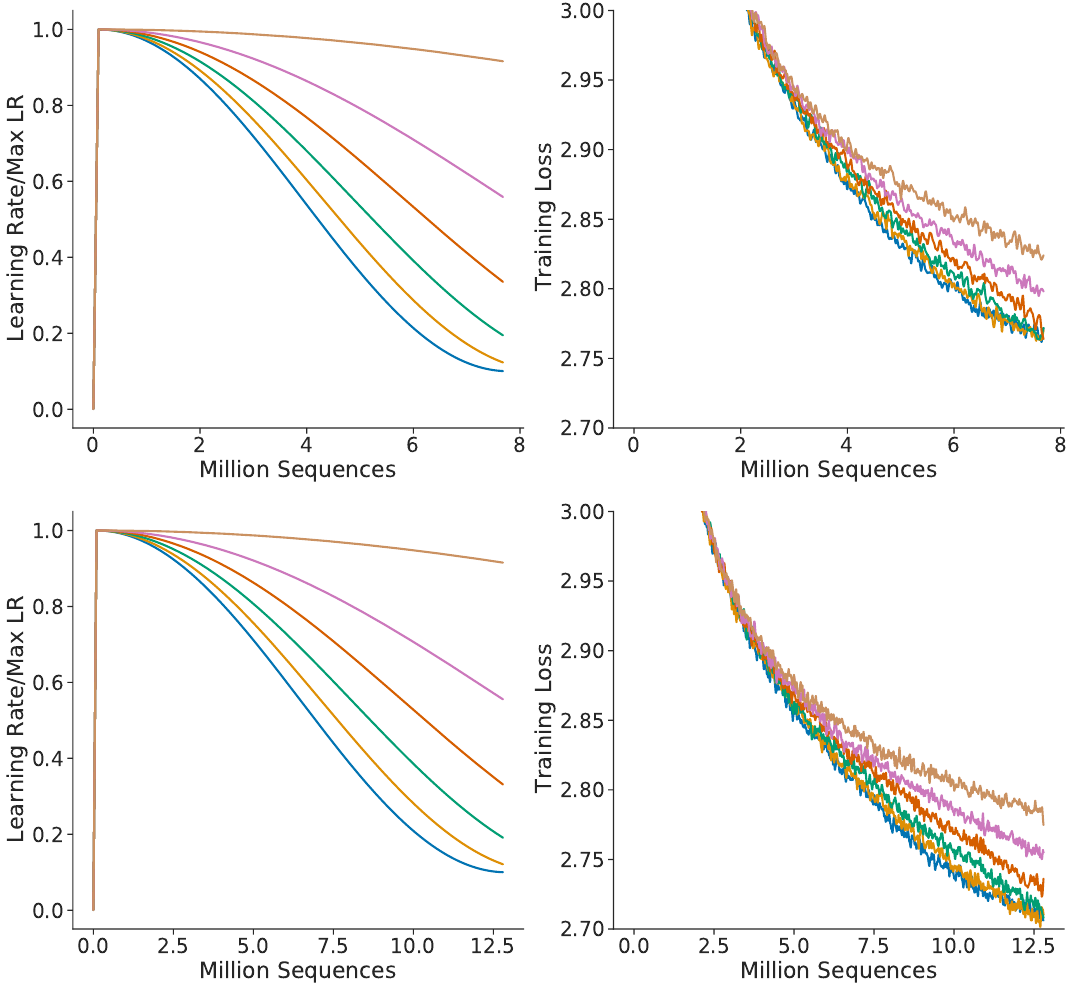
Chinchilla 余弦調(diào)度消融研究
他們指出,當(dāng)學(xué)習(xí)率曲線沒有延展時(shí),能實(shí)現(xiàn)最低的損失。這得到了圖表的支持,但其中也有不對(duì)勁的地方。在讀取了 600 萬(wàn) token 后,上圖模型的訓(xùn)練損失低于 2.8;與此同時(shí),在相同的位置,下圖模型的訓(xùn)練損失還更好。然而這兩個(gè)模型的差異僅僅是余弦調(diào)度!由于下圖模型注定會(huì)處理更多訓(xùn)練數(shù)據(jù),所以就計(jì)算了「未拉伸的」余弦調(diào)度更多步驟,這實(shí)際上產(chǎn)生了拉伸效果。如果學(xué)習(xí)率遵循分配給更少訓(xùn)練步驟的余弦調(diào)度,其在同等訓(xùn)練時(shí)間下的損失會(huì)更低。
更廣泛地說(shuō),這會(huì)引出一個(gè)有待解答的問題:如果余弦調(diào)度不是最優(yōu)的,那么曲線的尾部形狀應(yīng)該是什么樣子?