在不平衡數據上訓練的分類算法往往導致預測質量差。模型嚴重偏向多數類，忽略了對許多用例至關重要的少數例子。這使得模型對于涉及罕見但高優先級事件的現實問題來說不切實際。

過采樣提供了一種在模型訓練開始之前重新平衡類的方法。通過復制少數類數據點，過采樣平衡了訓練數據，防止算法忽略重要但數量少的類。雖然存在過擬合風險，但過采樣可以抵消不平衡學習的負面影響，可以讓機器學習模型獲得解決關鍵用例的能力

常見的過采樣技術包括隨機過采樣、SMOTE(合成少數過采樣技術)和ADASYN(不平衡學習的自適應合成采樣方法)。隨機過采樣簡單地復制少數樣本，而SMOTE和ADASYN策略性地生成合成的新數據來增強真實樣本。

什么是過采樣

過采樣是一種數據增強技術，用于解決類不平衡問題（其中一個類的數量明顯超過其他類）。它旨在通過擴大屬于代表性不足的類別的樣本量來重新平衡訓練數據分布。

過采樣通過復制現有樣本或生成合成的新數據點來增加少數類樣本。這是通過復制真實的少數觀察結果或根據真實世界的模式創建人工添加來實現的。

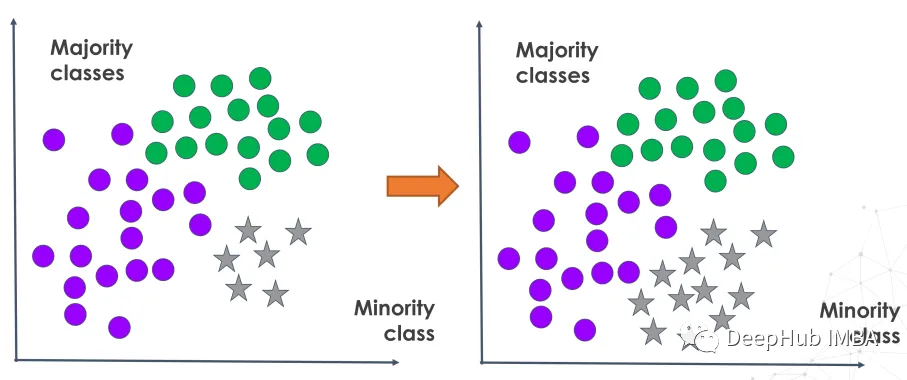
在模型訓練之前通過過采樣放大代表性不足的類別，這樣模型學習可以更全面地代表所有類別，而不是嚴重傾向于占主導地位的類別。這改進了用于解決涉及檢測重要但不常見事件的需求的各種評估度量。

為什么要過采樣

當處理不平衡數據集時，我們通常對正確分類少數類感興趣。假陰性(即未能檢測到少數類別)的成本遠高于假陽性(即錯誤地將樣本識別為屬于少數類別)的成本。

傳統的機器學習算法，如邏輯回歸和隨機森林目標優化假設均衡類分布的廣義性能指標。所以在傾斜數據上訓練的模型往往非常傾向于數量多的類，而忽略了數量少但重要的類的模式。

通過對少數類樣本進行過采樣，數據集被重新平衡，以反映所有結果中更平等的錯誤分類成本。這確保了分類器可以更準確地識別代表性不足的類別，并減少代價高昂的假陰性。

過采樣VS欠采樣

過采樣和欠采樣都是通過平衡訓練數據分布來解決類不平衡的技術。他們以相反的方式達到這種平衡。

過采樣通過復制或生成新樣本來增加少數類來解決不平衡問題。而欠采樣通過減少代表性過高的多數類別中的樣本數量來平衡類別。

當大多數類有許多冗余或相似的樣本或處理龐大的數據集時，就可以使用欠采樣。但是它欠采樣有可能導致信息的丟失，從而導致有偏見的模型。

當數據集很小并且少數類的可用樣本有限時，就可以使用過采樣。由于數據重復或創建了不代表真實數據的合成數據，它也可能導致過擬合。

下面我們將探討不同類型的過采樣方法。

1、隨機過采樣

隨機過采樣隨機復制少數類樣本以平衡類分布，所以他的實現非常簡單。它以隨機的方式從代表性不足的類別中選擇現有的樣本，并在不改變的情況下復制它們。這樣做的好處是當數據集規模較小時，可以有效地提高少數觀測值，而不需要收集額外的真實世界數據。

imbalanced-learn 庫中的randomoverampler可以實現過采樣的過程。

from imblearn.over_sampling import RandomOverSampler
 from imblearn.pipeline import make_pipeline
 
 X, y = create_dataset(n_samples=100, weights=(0.05, 0.25, 0.7))
 
 fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(15, 7))
 
 clf.fit(X, y)
 plot_decision_function(X, y, clf, axs[0], title="Without resampling")
 
 sampler = RandomOverSampler(random_state=0)
 model = make_pipeline(sampler, clf).fit(X, y)
 plot_decision_function(X, y, model, axs[1],
                        f"Using {model[0].__class__.__name__}")
 
 fig.suptitle(f"Decision function of {clf.__class__.__name__}")
 fig.tight_layout()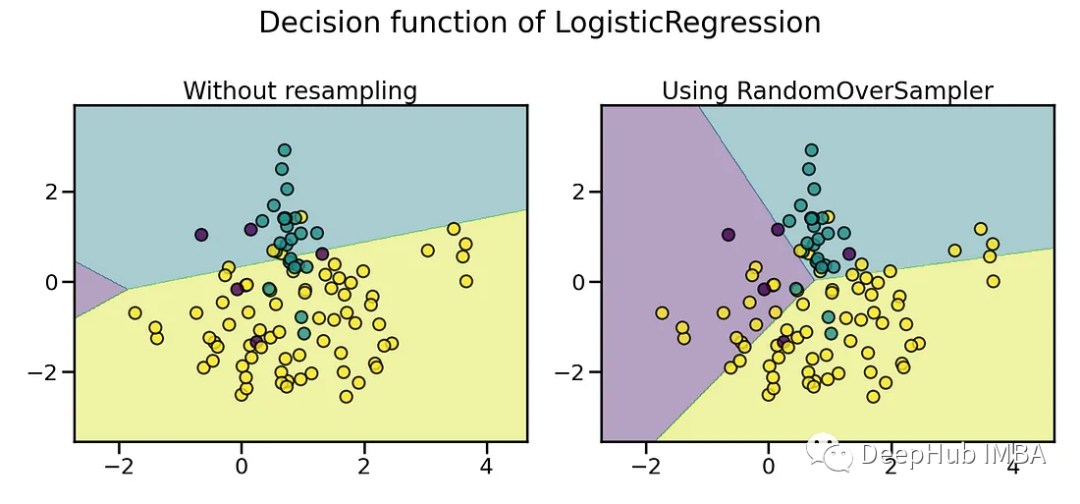

上圖可以看到，通過復制樣本，使得少數類的在分類結果中被正確的識別了。

2、平滑的自舉過采樣

帶噪聲的隨機過采樣是簡單隨機過采樣的改進版本，目的是解決其過擬合問題。這種方法不是精確地復制少數類樣本，而是通過將隨機性或噪聲引入現有樣本中來合成新的數據點。

默認情況下，隨機過采樣會產生自舉。收縮參數則在生成的數據中添加一個小的擾動來生成平滑的自舉。下圖顯示了兩種數據生成策略之間的差異。

fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(15, 7))
 
 sampler.set_params(shrinkage=1)
 plot_resampling(X, y, sampler, ax=axs[0], title="Normal bootstrap")
 
 sampler.set_params(shrinkage=0.3)
 plot_resampling(X, y, sampler, ax=axs[1], title="Smoothed bootstrap")
 
 fig.suptitle(f"Resampling with {sampler.__class__.__name__}")
 fig.tight_layout()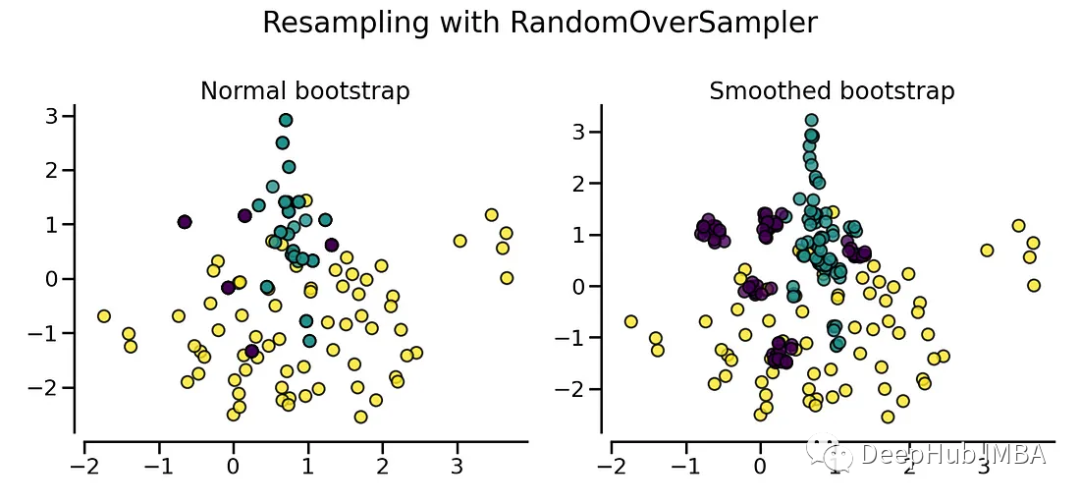

平滑的自舉插值不是任意重復少數觀察樣本，而是創建新的數據點，這些數據點是來自真實樣本的特征向量的組合或插值。這樣做的效果是，通過數據擴展而不是直接復制，將可用的少數數據擴展到原始記錄之外。

插值的數據點是“平滑”的組合，它們占據真實樣本周圍的特征空間，而不是覆蓋在它們上面。因此與隨機過采樣相比，平滑自舉過采樣產生了更多新的合成少數樣本。這有助于解決來自重復技術的過擬合問題，同時仍然平衡類分布。

隨機過采樣的好處是它是一種非常直接和簡單的技術。它不需要復雜的算法或對數據底層分布的假設。因此，它可以很容易地應用于任何不平衡的數據集，而不需要特殊的先驗知識。

但是隨機過采樣也受到過擬合可能性的限制。由于它只是復制了現有的少數樣本的例子，而不是產生真正的新樣本，所以觀察結果并沒有提供關于代表性不足的類的額外信息細節。而且這種重復也有可能放大了訓練數據中的噪聲，而不是更全面地正確表征少數類。

這樣訓練出來的模型模型可能會過度定制初始數據集的特定細微差別，而不是捕獲真正的底層模式。這就限制了它們在面對新的未知數據時的泛化能力。

3、SMOTE

SMOTE(Synthetic Minority Oversampling Technique)是一種廣泛應用于機器學習中緩解類失衡問題的過采樣方法。

SMOTE背后的關鍵概念是，它通過插值而不是復制，為代表性不足的類生成新的合成數據點。它隨機選擇一個少數類觀測值，并根據特征空間距離確定其最近的k個相鄰少數類樣本。

然后通過在初始樣本和k個鄰居之間進行插值生成新的合成樣本。這種插值策略合成了新的數據點，這些數據點填充了真實觀測之間的區域，在功能上擴展了可用的少數樣本，而不需要復制原始記錄。

SMOTE 的工作流程如下：

1. 對于每個少數類樣本，計算其在特征空間中的 K 近鄰樣本，K 是一個用戶定義的參數。
2. 針對每個少數類樣本，從其 K 近鄰中隨機選擇一個樣本。
3. 對于選定的近鄰樣本和當前少數類樣本，計算它們之間的差異，并乘以一個隨機數（通常在 [0, 1] 之間），將該乘積加到當前樣本上，生成新的合成樣本。
4. 重復上述步驟，為每個少數類樣本生成一定數量的合成樣本。
5. 將生成的合成樣本與原始數據合并，用于訓練分類模型。

SMOTE 的關鍵優勢在于通過合成樣本能夠增加數據集中少數類的樣本數量，而不是簡單地重復已有的樣本。這有助于防止模型對于過擬合少數類樣本，同時提高對未見過樣本的泛化性能。

SMOTE 也有一些變種，例如 Borderline-SMOTE 和 ADASYN，它們在生成合成樣本時考慮了樣本的邊界情況和密度信息，進一步改進了類別不平衡問題的處理效果。

4、自適應合成采樣(ADASYN)

自適應合成采樣（Adaptive Synthetic Sampling，ADASYN） 是一種基于數據重采樣的方法，它通過在特征空間中對少數類樣本進行合成生成新的樣本，從而平衡不同類別的樣本分布。與簡單的過采樣方法（如重復少數類樣本）不同，ADASYN 能夠根據樣本的密度分布自適應地生成新的樣本，更注重在密度較低的區域生成樣本，以提高模型對邊界區域的泛化能力。

ADASYN 的工作流程如下：

1. 對于每個少數類樣本，計算其在特征空間中的 K 近鄰樣本，K 是一個用戶定義的參數。
2. 計算每個少數類樣本與其 K 近鄰樣本之間的樣本密度比，該比例用于表示樣本所在區域的密度。
3. 對于每個少數類樣本，根據其樣本密度比，生成一定數量的合成樣本，使得合成樣本更集中在密度較低的區域。
4. 將生成的合成樣本與原始數據合并，用于訓練分類模型。

ADASYN 的主要目標是在增加少數類樣本的同時，盡量保持分類器在決策邊界附近的性能。也就是說如果少數類的一些最近鄰來自相反的類，來自相反類的鄰居越多，它就越有可能被用作模板。在選擇模板之后，它通過在模板和同一類的最近鄰居之間進行插值來生成樣本。

生成方法對比

from imblearn import FunctionSampler # to use a idendity sampler
 from imblearn.over_sampling import ADASYN, SMOTE
 
 X, y = create_dataset(n_samples=150, weights=(0.1, 0.2, 0.7))
 
 fig, axs = plt.subplots(nrows=2, ncols=2, figsize=(15, 15))
 
 samplers = [
    FunctionSampler(),
    RandomOverSampler(random_state=0),
    SMOTE(random_state=0),
    ADASYN(random_state=0),
 ]
 
 for ax, sampler in zip(axs.ravel(), samplers):
    title = "Original dataset" if isinstance(sampler, FunctionSampler) else None
    plot_resampling(X, y, sampler, ax, title=title)
 fig.tight_layout()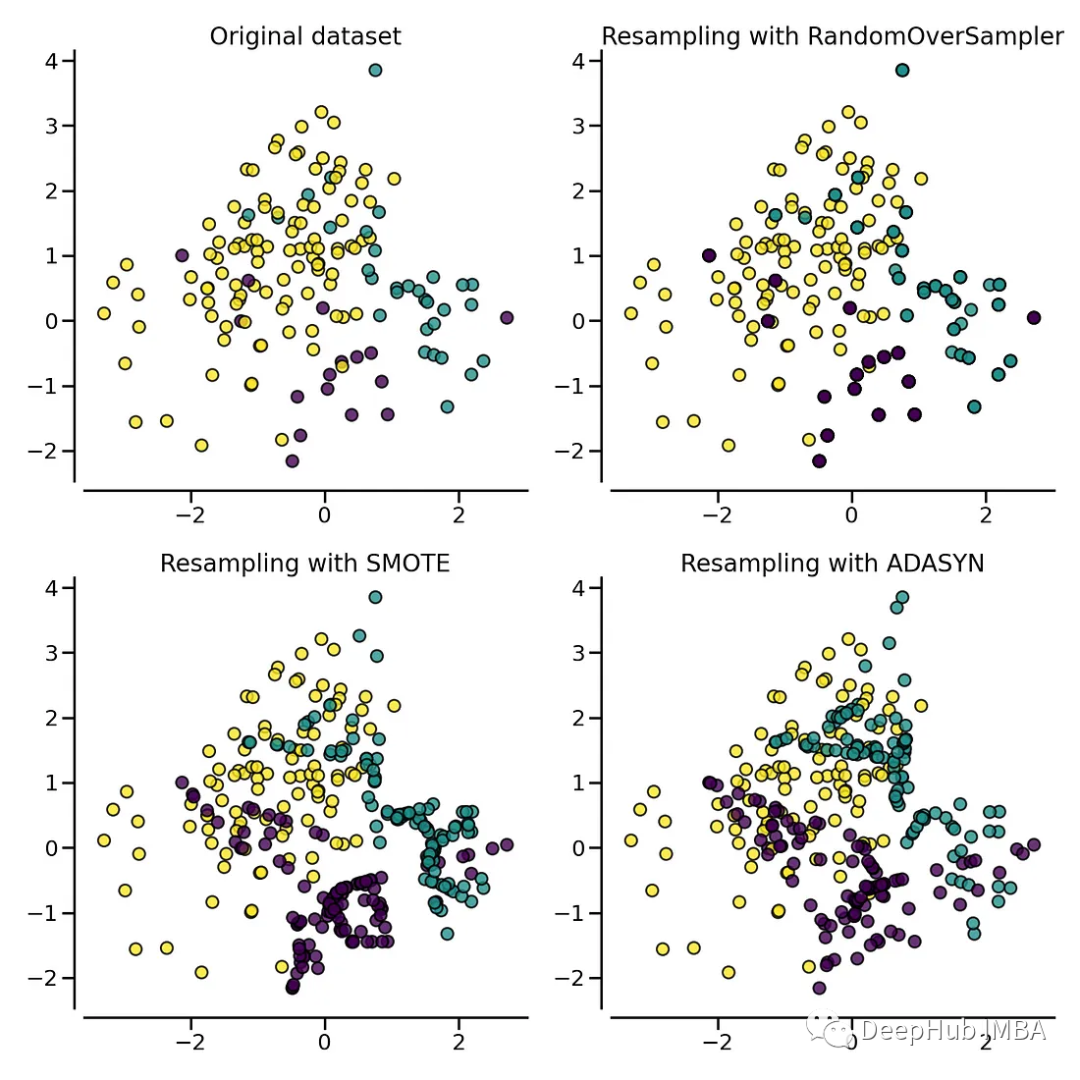

上圖可以看到ADASYN和SMOTE之間的區別。ADASYN將專注于難以分類的樣本，而常規SMOTE將不做任何區分。

下面我們看看不同算法的分類結果

X, y = create_dataset(n_samples=150, weights=(0.05, 0.25, 0.7))
 
 fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(20, 6))
 
 models = {
    "Without sampler": clf,
    "ADASYN sampler": make_pipeline(ADASYN(random_state=0), clf),
    "SMOTE sampler": make_pipeline(SMOTE(random_state=0), clf),
 }
 
 for ax, (title, model) in zip(axs, models.items()):
    model.fit(X, y)
    plot_decision_function(X, y, model, ax=ax, title=title)
 
 fig.suptitle(f"Decision function using a {clf.__class__.__name__}")
 fig.tight_layout()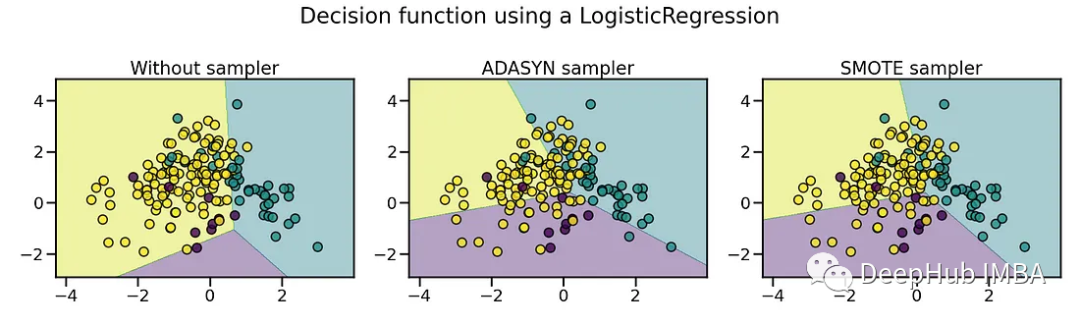

可以看到如果不進行過采樣，那么少數類基本上沒法區分。通過過采樣的技術，少數類得到了有效的區分。

SMOTE對所有的少數類樣本平等對待，不考慮它們之間的分布密度。ADASYN考慮到每個少數類樣本的鄰近樣本數量，使得對于那些鄰近樣本較少的少數類樣本，生成更多的合成樣本，以便更好地覆蓋整個決策邊界。

但是這兩個算法還要根據實際應用時選擇，比如上圖中黃色和藍色的決策邊界變化的影響需要實際測算后才能判斷那個算法更適合當前的應用。