突破 Pytorch 核心點,損失函數 !!!
嗨,我是小壯!
今天聊聊關于 PyTorch 中關于損失的內容。
損失函數通常用于衡量模型預測和實際目標之間的差異,并且在訓練神經網絡時,目標是最小化這個差異。
下面列舉了關于PyTorch中損失函數的詳細說明,大家可以在編輯器中敲出來,并且理解其使用方式。

損失函數
在PyTorch中,損失函數通常被定義為torch.nn.Module的子類。這些子類實現了損失函數的前向計算以及一些額外的方法。在使用損失函數之前,首先需要導入PyTorch庫:
import torch
import torch.nn as nn常見的損失函數
(1) 交叉熵損失函數(CrossEntropyLoss)
交叉熵損失函數通常用于分類問題。在訓練過程中,它幫助我們度量模型輸出的概率分布與實際標簽之間的差異。
criterion = nn.CrossEntropyLoss()(2) 均方誤差損失函數(MSELoss)
均方誤差損失函數常用于回歸問題,其中模型的輸出是一個連續值。
criterion = nn.MSELoss()損失函數的使用
(1) 計算損失
在訓練過程中,通過將模型的輸出和實際標簽傳遞給損失函數來計算損失:
# 假設模型輸出為output,實際標簽為target
loss = criterion(output, target)(2) 清零梯度
在每一次迭代之前,務必清零模型參數的梯度,以免梯度累積。
optimizer.zero_grad()(3) 反向傳播和參數更新
通過反向傳播計算梯度,并使用優化器更新模型參數:
loss.backward()
optimizer.step()一個案例
以下是一個簡單的示例,演示了如何使用PyTorch進行簡單的線性回歸:
import torch
import torch.nn as nn
import torch.optim as optim
import matplotlib.pyplot as plt
# 數據準備
x_train = torch.tensor([[1.0], [2.0], [3.0]])
y_train = torch.tensor([[2.0], [4.0], [6.0]])
# 模型定義
class LinearRegressionModel(nn.Module):
def __init__(self):
super(LinearRegressionModel, self).__init__()
self.linear = nn.Linear(1, 1)
def forward(self, x):
return self.linear(x)
model = LinearRegressionModel()
# 損失函數和優化器定義
criterion = nn.MSELoss()
optimizer = optim.SGD(model.parameters(), lr=0.01)
# 訓練過程
epochs = 1000
losses = [] # 用于存儲每輪訓練的損失值
for epoch in range(epochs):
# Forward pass
predictions = model(x_train)
loss = criterion(predictions, y_train)
# Backward pass
optimizer.zero_grad()
loss.backward()
optimizer.step()
# 記錄損失值
losses.append(loss.item())
# 打印訓練過程中的損失
if (epoch + 1) % 100 == 0:
print(f'Epoch [{epoch+1}/{epochs}], Loss: {loss.item():.4f}')
# 繪制損失函數隨時間的變化
plt.plot(losses, label='Training Loss')
plt.xlabel('Epochs')
plt.ylabel('Loss')
plt.title('Training Loss over Time')
plt.legend()
plt.show()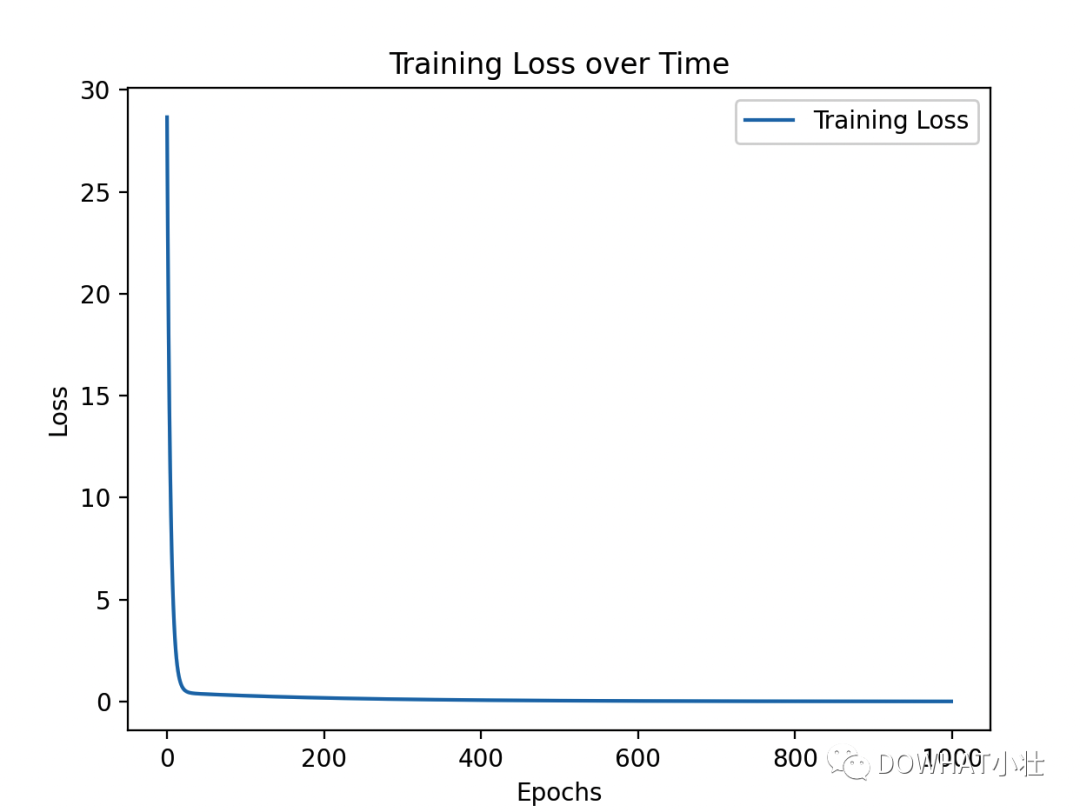
我們在訓練神經網絡時,通常會關心模型在訓練數據上的性能,而損失函數是一個用于度量模型性能的指標。損失函數的值越小,表示模型的預測越接近實際標簽,因此我們的目標是通過調整模型的參數來最小化損失函數。
代碼中,我們使用了一個簡單的線性回歸模型,該模型通過訓練數據(x_train和y_train)來學習如何預測目標值。為了衡量模型的性能,我們選擇了均方誤差(MSE)作為損失函數。
代碼的主要部分包括:
- 模型定義:我們定義了一個簡單的線性回歸模型,它包含一個線性層(nn.Linear)。
- 損失函數和優化器定義:我們選擇均方誤差損失函數(nn.MSELoss)作為度量模型性能的指標,并使用隨機梯度下降優化器(optim.SGD)來調整模型參數以最小化損失函數。
- 訓練過程:通過多次迭代訓練數據,模型逐漸調整參數,以使損失函數逐漸減小。在每次迭代中,我們計算損失、進行反向傳播和參數更新。訓練過程中的損失值被記錄下來,以便后續繪制圖表。
- 繪制損失函數圖表:我們使用matplotlib庫繪制了損失函數隨訓練輪次的變化圖表。圖表的橫軸是訓練輪次(epochs),縱軸是損失函數的值。通過觀察圖表,我們可以了解模型在訓練過程中學到的程度。
這個圖表是一個直觀的方式,幫助我們了解神經網絡的訓練進展。在實際的操作中,幫助我們修改和優化其中的邏輯。