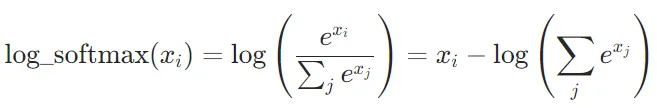在深度學習和機器學習領域，損失函數是模型優化的核心工具之一。它不僅決定了模型的訓練方向，還直接影響模型的性能和泛化能力。隨著大語言模型（LLM）的興起，對損失函數的理解和應用變得更加重要。本文將深入探討兩種常用的損失函數——KL散度和交叉熵損失，并分析它們在實際應用中的區別和聯系。

一、KL散度

KL散度（Kullback-Leibler Divergence）用于衡量兩個概率分布之間的相似性，常用于知識蒸餾（Knowledge Distillation）和對抗訓練（Adversarial Training）等任務。其公式為：

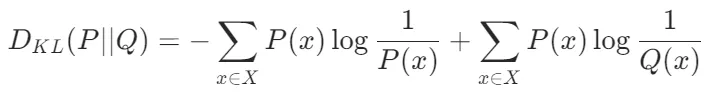
應用場景

• 知識蒸餾：在知識蒸餾中，KL散度損失用于衡量學生模型的輸出分布與教師模型的輸出分布之間的差異。通過最小化這種差異，學生模型可以學習到教師模型的“知識”，從而提高性能。
• 對抗訓練：KL散度損失可以用于衡量模型在對抗樣本上的輸出分布與真實分布之間的差異，從而增強模型的魯棒性。

物理意義

KL散度（Kullback-Leibler Divergence）的物理意義可以從信息論和統計學的角度來理解，它是一種衡量兩個概率分布之間差異的工具，具有重要的理論和實際應用價值。

1. 信息論角度
   KL散度最初來源于信息論，用于衡量兩個概率分布之間的“信息差距”。具體來說，它量化了當我們用一個概率分布Q來近似另一個概率分布P時，所導致的額外信息損失。這種信息損失可以理解為編碼數據時所需的“額外比特數”，即使用Q來編碼P數據時的效率損失。
   從熵的角度來看，KL散度可以表示為真實分布P的熵與P和Q之間的交叉熵的差值。因此，KL散度實際上衡量了使用Q而非P所引入的額外不確定性。
2. 非對稱性和非負性
   KL散度具有兩個關鍵性質：
   非負性：KL散度始終大于等于零，表示兩個分布之間的差異不會產生“負的信息損失”。
   非對稱性：KL散度是不對稱的，即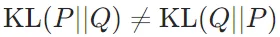。這意味著選擇不同的分布作為真實分布和近似分布會導致不同的結果。

KL散度定義為使用Q來編碼P時的額外信息量怎么解讀

1. 信息量與編碼
   在信息論中，信息量通常與編碼長度相關。對于一個概率分布P，如果某個事件x發生的概率為P(x)，那么該事件的信息量可以表示為?log?P(x)。這意味著概率越小的事件，其信息量越大，因為它們更“出人意料”。
2. 使用Q編碼P
   當我們使用另一個概率分布Q來編碼P時，事件x的編碼長度將基于Q(x)而不是P(x)。因此，事件x的編碼長度變為?logQ(x)。
3. 額外信息量
   使用Q來編碼P時的額外信息量，就是基于Q的編碼長度與基于P的編碼長度之間的差值。對于所有可能的事件x，這個差值的期望值就是KL散度：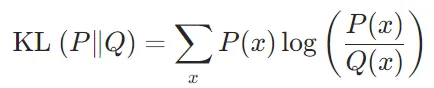
   
   這個公式可以解釋為：對于每個事件x，我們計算使用Q編碼x時比使用P編碼x多出的信息量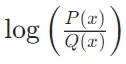，然后根據P的概率分布對所有事件求和。

4. 直觀理解

• 如果P(x)和Q(x)非常接近，那么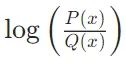接近零，表示使用Q編碼P時的額外信息量很小。
• 如果P(x)和Q(x)差距很大，那么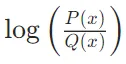的絕對值很大，表示使用Q編碼P時的額外信息量很大。

二、交叉熵損失

交叉熵損失函數（Cross-Entropy Loss Function）主要用于衡量模型預測的概率分布與真實標簽之間的差異。

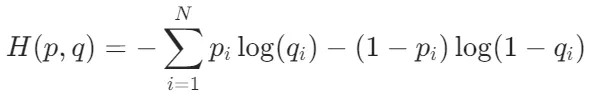
其中，p表示真實標簽，q表示模型預測的標簽，N表示樣本數量。該公式可以看作是一個基于概率分布的比較方式，即將真實標簽看做一個概率分布，將模型預測的標簽也看做一個概率分布，然后計算它們之間的交叉熵。

應用場景

• 分類問題：在分類問題中，它通常用于衡量模型的預測分布與實際標簽分布之間的差異。
• 下一個單詞預測：在語言模型中通過最小化模型預測的概率分布與真實單詞的概率分布之間的差異，用于下一個單詞預測任務。

物理意義

交叉熵損失函數本質上是衡量兩個概率分布之間的差異，這種差異反映了信息的“不確定性”或“信息量”。

1. 信息量與不確定性
   在信息論中，熵（Entropy）是衡量信息不確定性的一個重要概念。熵越高，表示信息的不確定性越大；熵越低，表示信息的不確定性越小。例如，一個均勻分布的隨機變量（如拋硬幣）具有較高的熵，因為它包含更多的不確定性；而一個確定性事件（如拋一枚兩面都是正面的硬幣）的熵為零，因為它沒有任何不確定性。
   交叉熵損失函數的核心是交叉熵（Cross-Entropy），它衡量的是模型預測的概率分布與真實分布之間的信息量。具體來說，交叉熵損失反映了模型預測分布對真實分布的“驚訝程度”或“不確定性”。

• 如果模型的預測分布與真實分布完全一致，交叉熵損失會達到最小值。
• 如果模型的預測分布與真實分布相差很大，交叉熵損失會很大，表示模型對真實結果感到“非常驚訝”。

2. 信息編碼與傳輸
   從信息編碼的角度來看，交叉熵損失也可以理解為一種“編碼代價”。假設我們用模型預測的概率分布來編碼真實數據，交叉熵損失表示了這種編碼所需的“平均比特數”。
   真實分布P表示數據的真實生成過程，模型預測的分布Q表示模型對數據生成過程的估計。如果Q與P非常接近，那么用Q來編碼P所需的信息量就會很少（即交叉熵損失很小）。反之，如果Q與P差距很大，編碼所需的比特數就會很多（即交叉熵損失很大）。
3. 數學上的直觀理解
   假設我們有一個二分類問題，真實標簽為y∈{0,1}，模型預測為正類的概率為p。交叉熵損失可以表示為：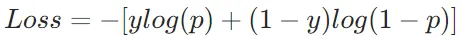 
   
   從這個公式可以看出，交叉熵損失懲罰了模型對真實結果的“不確定性”（即p遠離真實標簽）。當模型預測越準確時，損失越小，這與信息論中“減少不確定性”的目標一致。

• 如果真實標簽y=1，損失為?log(p)。此時，p越接近 1（即預測越準確），損失越小。
• 如果真實標簽y=0，損失為?log(1?p)。此時，p越接近 0（即預測越準確），損失越小。

分類問題為什么用交叉熵損失函數不用均方誤差（MSE）

交叉熵損失函數通常在分類問題中使用，而均方誤差（MSE）損失函數通常用于回歸問題。這是因為分類問題和回歸問題具有不同的特點和需求。

分類問題的目標是將輸入樣本分到不同的類別中，輸出為類別的概率分布。交叉熵損失函數可以度量兩個概率分布之間的差異，使得模型更好地擬合真實的類別分布。它對概率的細微差異更敏感，可以更好地區分不同的類別。此外，交叉熵損失函數在梯度計算時具有較好的數學性質，有助于更穩定地進行模型優化。

相比之下，均方誤差（MSE）損失函數更適用于回歸問題，其中目標是預測連續數值而不是類別。MSE損失函數度量預測值與真實值之間的差異的平方，適用于連續數值的回歸問題。在分類問題中使用MSE損失函數可能不太合適，因為它對概率的微小差異不夠敏感，而且在分類問題中通常需要使用激活函數（如sigmoid或softmax）將輸出映射到概率空間，使得MSE的數學性質不再適用。

綜上所述，交叉熵損失函數更適合分類問題，而MSE損失函數更適合回歸問題。

CrossEntropyLoss基于pytorch的源代碼實現

1. CrossEntropyLoss的實現原理
   CrossEntropyLoss的計算過程可以分為兩步：log_softmax：對模型的輸出應用log_softmax，將輸出轉換為對數概率分布。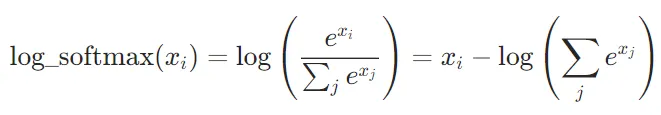

NLLLoss：計算負對數似然損失，即對真實標簽對應的對數概率取負值。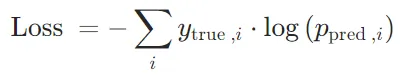

   數學公式可以表示為：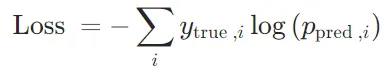
   
   其中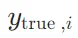，是真實標簽（通常是 one-hot 編碼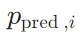），是模型預測的類別概率。
2. PyTorch 源代碼中的實現

# PyTorch 的 CrossEntropyLoss 實現
class CrossEntropyLoss(torch.nn.Module):
    def __init__(self, weight=None, size_average=None, ignore_index=-100, reductinotallow='mean'):
        super(CrossEntropyLoss, self).__init__()
        self.weight = weight
        self.ignore_index = ignore_index
        self.reduction = reduction
    def forward(self, input, target):
        return F.cross_entropy(input, target, weight=self.weight, ignore_index=self.ignore_index, reductinotallow=self.reduction)

在torch.nn.functional.cross_entropy中，實際調用了log_softmax和nll_loss：

def cross_entropy(input, target, weight=None, size_average=None, ignore_index=-100, reductinotallow='mean'):
    return F.nll_loss(F.log_softmax(input, 1), target, weight=weight, size_average=size_average, ignore_index=ignore_index, reductinotallow=reduction)

三、KL散度與交叉熵的區別

定義上的區別

• KL散度：KL散度是衡量兩個概率分布P和Q之間的差異的度量。它定義為使用Q來編碼P時的額外信息量，即P和Q的交叉熵與P的熵之差。
• 交叉熵：交叉熵是衡量使用一個概率分布Q來編碼另一個概率分布P時所需的平均信息量。

應用上的區別

• KL散度：KL散度在深度學習中常用于衡量兩個概率分布之間的差異，如在變分推斷、生成模型（如VAE）、強化學習等領域。它也用于檢測數據分布的漂移。
• 交叉熵：交叉熵在深度學習中主要用作損失函數，特別是在分類任務中。它用于衡量模型預測的概率分布與真實標簽的概率分布之間的差異，從而指導模型的優化。

KL散度與交叉熵的關系

交叉熵可以表示為KL散度與真實分布的熵之和：

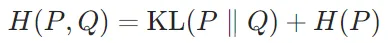
其中H(P)是真實分布P的熵。因此，最小化交叉熵等價于最小化KL散度，因為真實分布的熵是固定的。

四、其他

多任務學習各loss差異過大怎樣處理

多任務學習中，如果各任務的損失差異過大，可以通過動態調整損失權重、使用任務特定的損失函數、改變模型架構或引入正則化等方法來處理。目標是平衡各任務的貢獻，以便更好地訓練模型。

如果softmax的e次方超過float的值了怎么辦

1. 可以使用數值穩定性技巧來避免溢出。具體來說，可以在計算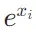之前從每個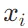中減去 x 中的最大值：
   
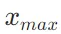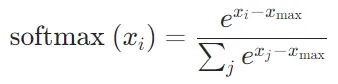
2. 使用對數概率來避免溢出
   對數函數log(x)具有將乘法運算轉換為加法運算的性質：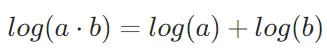
   
   這使得在處理非常小或非常大的概率值時，可以避免直接相乘導致的數值下溢（underflow）或上溢（overflow）。
   在計算交叉熵損失時，可以使用log_softmax，公式為：