Go與神經網絡:張量運算
0. 背景
2023年年初,我們很可能是見證了一次新工業革命的起點,也可能是見證了AGI(Artificial general intelligence,通用人工智能)[1]孕育的開始。ChatGPT應用以及后續GPT-4大模型的出現,其震撼程度遠超當年AlphaGo戰勝人類頂尖圍棋選手[2]。相對于AlphaGo在一個狹窄領域的建樹,ChatGPT則是以摧枯拉朽之勢橫掃幾乎所有腦力勞動行業。
如今大家更多將ChatGPT及相關應用當做生產力工具,作為程序員,自然會首當其沖的加入到借助AI提升生產力的陣營。但對于程序員來說,如果對一個計算機科學方面的技術沒有基本工作原理認知或是完全看不懂,那么就會有一種深深的危機感。
什么是深度學習、什么是神經網絡、什么是大模型、上千億的參數究竟指的是什么、什么是大模型的量化等都是縈繞在頭腦中的未知但又急切想知道的東西。
有人會說,深度學習發展都十多年了,現在學還來得及么?其實大多數人不是從事機器學習的,普通程序員只需要了解機器學習、深度學習(神經網絡)的基本運作原理即可。此外,有了ChatGPT相關工具后,獲取和理解知識的效率可以大幅提升,以前需要以年來計算學習新知識技能,現在可能僅需以月來計算,甚至更短。
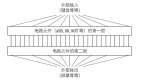
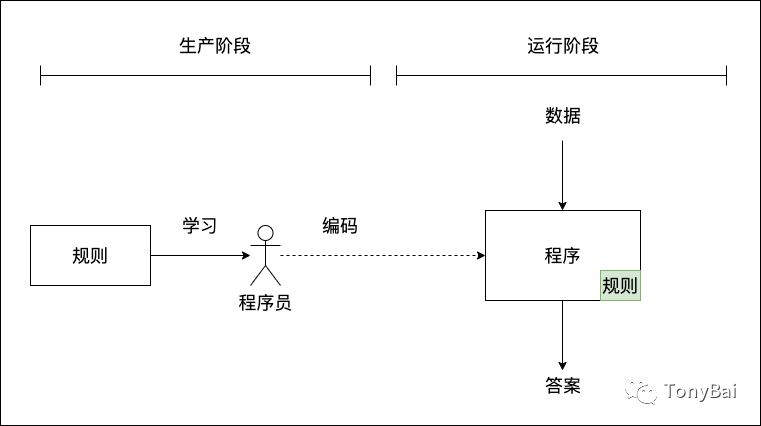
作為程序員,了解深度學習,了解神經網絡,其實也是去學習一種新的、完全不同于以往的編程范式。以前我們的編程范式是這樣的: 人類學習規則,然后通過手工編碼將規則內置到系統中,系統運行后,根據明確的規則對輸入數據做處理并給出答案(如下圖所示):
 圖片
圖片
這個大編程范式通常又細分為下面幾類,大家根據自己的喜好和工作要求選擇不同的編程范式以及編程語言:
- 命令式編程范式(C、Go等);
- 面向對象編程范式(Java、Ruby);
- 函數式編程范式(Haskell、Lisp、Clojure等);
- 聲明式編程范式(SQL)。
這類范式都歸屬于**符號主義人工智能(symbolic AI)**,即都是用來手工編寫明確的規則的。符號主義人工智能適合用來解決定義明確的邏輯問題,比如下國際象棋,但它難以給出明確規則來解決更復雜、更模糊的問題,比如圖像分類、語音識別或自然語言翻譯。
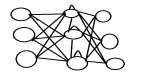
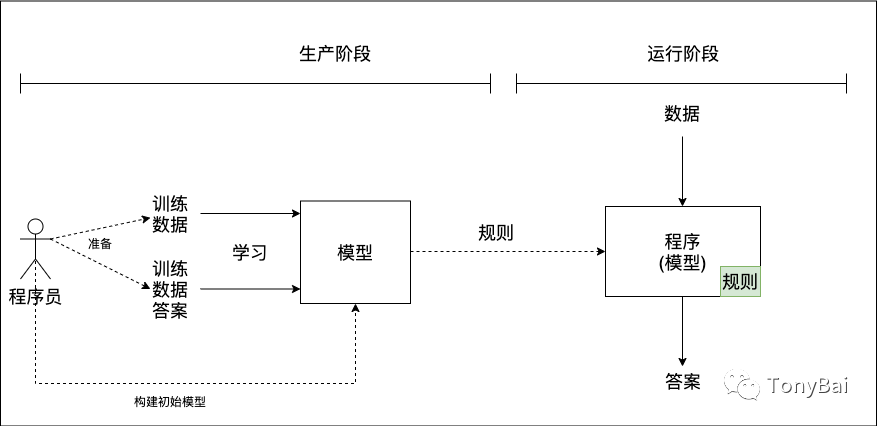
而機器學習或者說機器學習的結果人工神經網絡則是另外一種范式,如下圖所示:
 圖片
圖片
在這個范式中,程序員無需再學習什么規則,因為規則是模型自己通過數據學習來的。程序員只需準備好高質量的訓練數據以及對應的答案(標注),然后建立初始模型(初始神經網絡)即可,之后的事情就交給機器了(機器學習并非在數學方面做出什么理論突破,而是“蠻力出奇跡”一個生動案例)。模型通過數據進行自動訓練(學習)并生成包含規則的目標模型,而目標模型即程序。
了解兩類截然不同的范式之后,我再來澄清幾個問題:
- Go與神經網絡系列文章的目的?不是教你如何自己搞出一個大模型,而是將經典機器學習、深度學習(與建立人工神經網絡)的來龍去脈搞清楚。
- Why Go? 幫助Go程序員學習機器學習。雖然Python代碼看起來很容易理解,代碼量也會少很多(像Keras這樣的框架,甚至將training dataset都集成在框架中了)。
注:通過閱讀Python的機器學習/深度學習代碼,我覺得不會有什么語言可以代替Python作為AI主力了。用Python做數據準備、訓練模型簡直簡單的不要不要的了。
- 從何處開始?張量以及相關運算。
張量在深度學習中扮演著非常重要的角色,因為它們是存儲和處理數據的基本單位。張量可以看作是一個“容器”,可以表示向量、矩陣和更高維度的數據結構。深度學習中的神經網絡模型使用張量來表示輸入數據、模型參數和輸出結果,以及在計算過程中的各種中間變量。通過對張量進行數學運算和優化,深度學習模型能夠從大量的數據中學習到特征和規律,并用于分類、回歸、聚類等任務。因此,張量是深度學習中必不可少的概念之一。最流行的深度學習框架tensorflow都以tensor命名。我們也將從張量(tensor)出發進入機器學習和神經網絡世界。
不過大家要區分數學領域與機器學習領域張量在含義上的不同。在數學領域,張量是一個多維數組,而在機器學習領域,張量是一種數據結構,用于表示多維數組和高維矩陣。兩者的相同點在于都是多維數組,但不同點在于它們的應用場景和具體實現方式不同。如上一段描述那樣,在機器學習中,張量通常用于表示數據集、神經網絡的輸入和輸出等。
下面我們就來了解一下張量與張量的運算,包括如何創建張量、執行基本和高級張量操作,以及張量廣播(broadcast)與重塑(reshape)操作。
1. 理解張量
張量是目前所有機器學習系統都使用的基本數據結構。張量這一概念的核心在于,它是一個數據容器。它包含的數據通常是同類型的數值數據,因此它是一個同構的數字容器。
前面提到過,張量可以表示數字、向量、矩陣甚至更高維度的數據。很多語言采用多維數組來實現張量,不過也有采用平坦數組(flat array)來實現的,比如:gorgonia/tensor[3]。
無論實現方式是怎樣的,從邏輯上看,張量的表現是一致的,即張量是一個有如下屬性的同構數據類型。
1.1 階數(ndim)
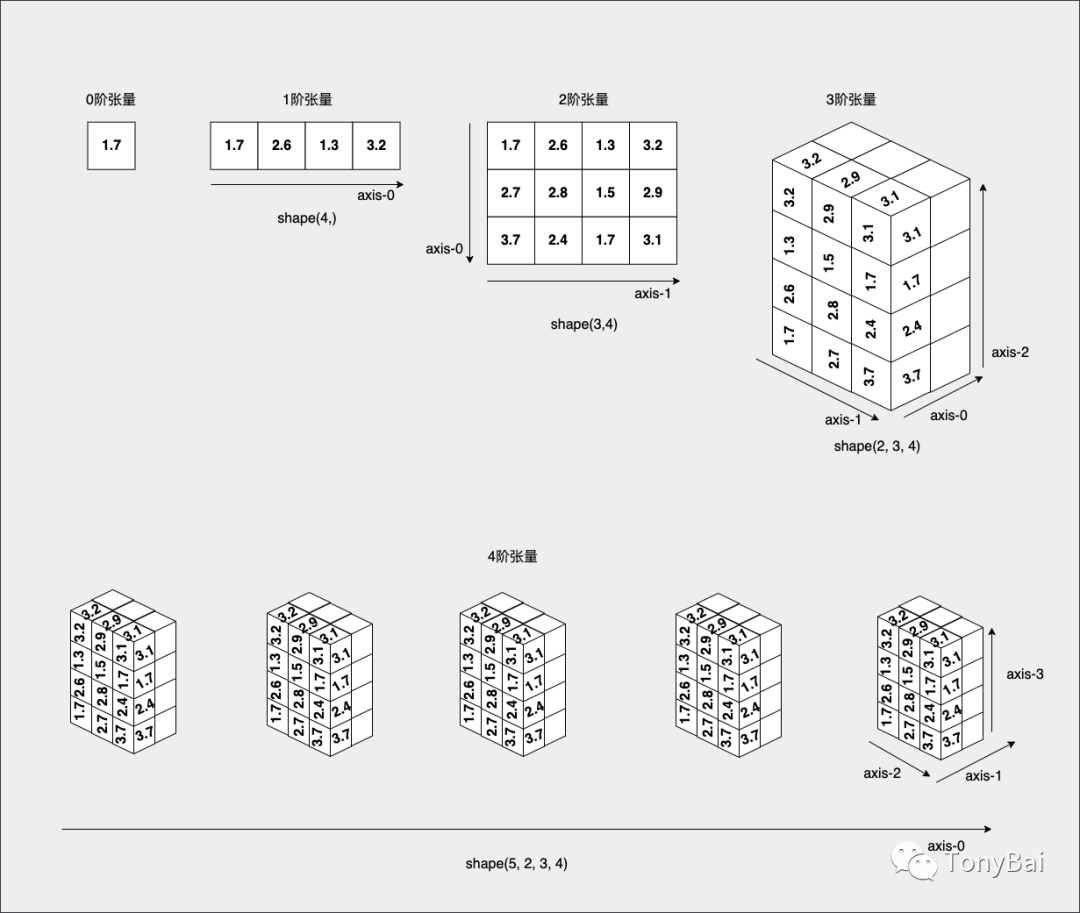
張量的維度通常叫作軸(axis),張量軸的個數也叫作階(rank)。下面是從0階張量到4階張量的示意圖:
 圖片
圖片
- 0階張量
僅包含一個數字的張量,也被稱為標量(scalar),也叫標量張量。0階張量有0個軸。
- 1階張量
1階張量,也稱為向量(vector),有一個軸。這個向量可以是n維向量,與張量的階數沒有關系。比如在上面圖中的一階張量表示的就是一個4維向量。所謂維度即沿著某個軸上的元素的個數。這個圖中一階張量表示的向量中有4個元素,因此是一個4維向量。
- 2階張量
2階張量,也稱為矩陣(matrix),有2個軸。在2階張量中,這兩個軸也稱為矩陣的行(axis-0)和列(axis-1),每個軸上的向量都有自己的維度。例如上圖中的2階張量的axis-0軸上有3個元素(每個元素又都是一個向量),因此是axis-0的維度為3,由此類推,axis-1軸的維度為4。
注:張量的軸的下標從0開始,如axis-0、axis-1、...、axis-n。
2階張量也可以看成是1階張量的數組。
- 3階或更高階張量
3階張量有3個軸,如上圖中的3階張量,可以看成是多個2階張量組成的數組。
以此類推,擴展至N階張量,可以看成是N-1階張量的數組。
1.2 形狀(shape)
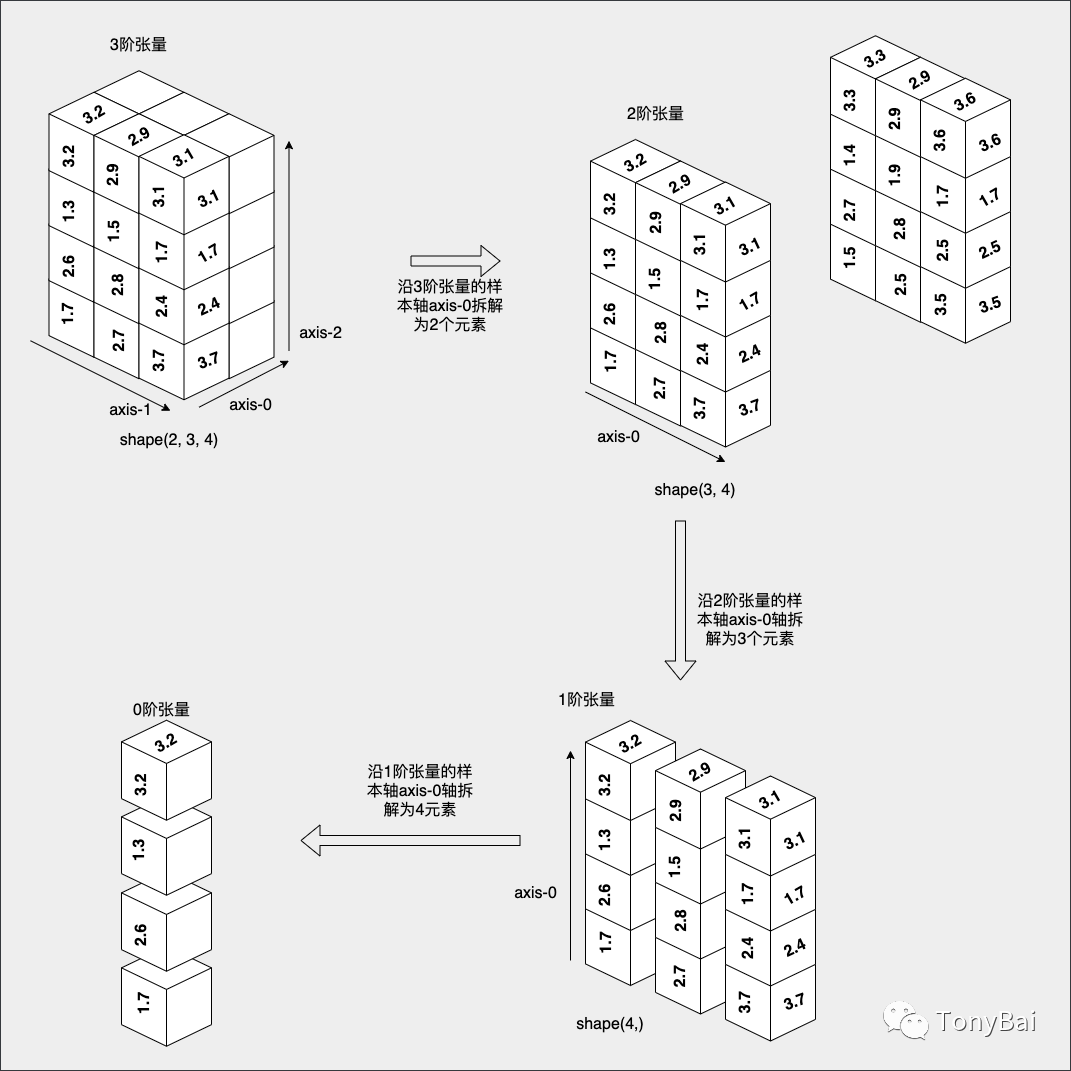
張量有一個屬性為shape,shape由張量每個軸上的維度(軸上元素的個數)組成。以上圖中的3階張量為例,其axis-0軸上有2個元素,axis-1軸上有3個元素,axis-2軸上有4個元素,因此該3階張量的shape為(2, 3, 4)。axis-0軸也被稱為樣本軸,下圖是按照每一級張量的樣本軸對張量做拆解的示意圖:
 圖片
圖片
我們首先對3階張量(shape(2,3,4))沿著其樣本軸方向進行拆解,我們將其拆解2個2階張量(shape(3,4))。接下來,我們對得到的2階張量進行拆解,同樣沿著其樣本軸方向拆解為3個1階張量(shape(4,))。我們看到,每個1階張量是一個4維向量,可拆解為4個0階張量。
1.3 元素數據類型dtype
張量是同構數據類型,無論是幾階張量,最終都是由一個個標量組合而成,標量的類型就是張量的元素數據類型(dtype),在上圖中,我們的張量的dtype為float32。浮點數與整型數是機器學習中張量最常用的元素數據類型。
了解了張量的概念與屬性后,我們就來看看在Go中如何創建張量。
2. 在Go中創建張量
Go提供了幾個機器學習庫,可以用來創建和操作張量。在Go中執行張量操作的兩個流行庫是Tensorflow[4]和Gorgonia[5]。
不過Tensorflow官方團隊已經不再對go binding API提供維護支持了(由Go社區第三方負責維護[6]),并且該binding需要依賴cgo調用tensorflow的庫,因此在本文中,我們使用gorgonia來定義張量以及進行張量運算。
Gorgonia提供了tensor包[7]用來定義tensor并提供基于tensor的基本運算函數。下面的例子使用tensor包定義了對應上面圖中1階到3階的三個張量:
// https://github.com/bigwhite/experiments/blob/master/go-and-nn/tensor-operations/tensor.go
package main
import (
"fmt"
"gorgonia.org/tensor"
)
func main() {
// define an one-rank tensor
oneRankTensor := tensor.New(tensor.WithBacking([]float32{1.7, 2.6, 1.3, 3.2}), tensor.WithShape(4))
fmt.Println("\none-rank tensor:")
fmt.Println(oneRankTensor)
fmt.Println("ndim:", oneRankTensor.Dims())
fmt.Println("shape:", oneRankTensor.Shape())
fmt.Println("dtype", oneRankTensor.Dtype())
// define an two-rank tensor
twoRankTensor := tensor.New(tensor.WithBacking([]float32{1.7, 2.6, 1.3, 3.2,
2.7, 2.8, 1.5, 2.9,
3.7, 2.4, 1.7, 3.1}), tensor.WithShape(3, 4))
fmt.Println("\ntwo-rank tensor:")
fmt.Println(twoRankTensor)
fmt.Println("ndim:", twoRankTensor.Dims())
fmt.Println("shape:", twoRankTensor.Shape())
fmt.Println("dtype", twoRankTensor.Dtype())
// define an three-rank tensor
threeRankTensor := tensor.New(tensor.WithBacking([]float32{1.7, 2.6, 1.3, 3.2,
2.7, 2.8, 1.5, 2.9,
3.7, 2.4, 1.7, 3.1,
1.5, 2.7, 1.4, 3.3,
2.5, 2.8, 1.9, 2.9,
3.5, 2.5, 1.7, 3.6}), tensor.WithShape(2, 3, 4))
fmt.Println("\nthree-rank tensor:")
fmt.Println(threeRankTensor)
fmt.Println("ndim:", threeRankTensor.Dims())
fmt.Println("shape:", threeRankTensor.Shape())
fmt.Println("dtype", threeRankTensor.Dtype())
}tensor.New接受一個變長參數列表,這里我們顯式傳入了存儲張量數據的平坦數組數據以及tensor的shape屬性,這樣我們便能得到一個滿足我們要求的tensor變量。運行上面程序,你將看到下面內容:
$ASSUME_NO_MOVING_GC_UNSAFE_RISK_IT_WITH=go1.20 go run tensor.go
one-rank tensor:
[1.7 2.6 1.3 3.2]
ndim: 1
shape: (4)
dtype float32
two-rank tensor:
?1.7 2.6 1.3 3.2?
?2.7 2.8 1.5 2.9?
?3.7 2.4 1.7 3.1?
ndim: 2
shape: (3, 4)
dtype float32
three-rank tensor:
?1.7 2.6 1.3 3.2?
?2.7 2.8 1.5 2.9?
?3.7 2.4 1.7 3.1?
?1.5 2.7 1.4 3.3?
?2.5 2.8 1.9 2.9?
?3.5 2.5 1.7 3.6?
ndim: 3
shape: (2, 3, 4)
dtype float32tensor.New返回的*tensor.Dense類型實現了fmt.Stringer接口,可以按shape形式打印出tensor,但是人類肉眼也就識別到3階tensor吧。3階以上的tensor輸出的格式用人眼識別和理解就有些困難了。
此外,我們看到Gorgonia的tensor包基于平坦的數組來存儲tensor數據,tensor包根據shape屬性對數組中數據做切分,劃分出不同軸上的數據。數組的元素類型可以自定義,如果我們使用float64的切片,那么tensor的dtype就為float64。
3. Go中的基本張量運算
現在我們知道了如何使用Gorgonia/tensor創建張量了,讓我們來探索Go中的一些基本張量運算。
3.1. 加法和減法
將兩個相同形狀(shape)的張量相加或相減是機器學習算法中的一個常見操作。在Go中,我們可以使用Gorgonia/tensor提供的Add和Sub函數進行加減操作。下面是一個使用tensor包進行加減運算的示例代碼片斷:
// https://github.com/bigwhite/experiments/blob/master/go-and-nn/tensor-operations/tensor_add_sub.go
func main() {
// define two two-rank tensor
ta := tensor.New(tensor.WithBacking([]float32{1.7, 2.6, 1.3, 3.2,
2.7, 2.8, 1.5, 2.9,
3.7, 2.4, 1.7, 3.1}), tensor.WithShape(3, 4))
fmt.Println("\ntensor a:")
fmt.Println(ta)
tb := tensor.New(tensor.WithBacking([]float32{1.7, 2.6, 1.3, 3.2,
2.7, 2.8, 1.5, 2.9,
3.7, 2.4, 1.7, 3.1}), tensor.WithShape(3, 4))
fmt.Println("\ntensor b:")
fmt.Println(ta)
tc, _ := tensor.Add(ta, tb)
fmt.Println("\ntensor a+b:")
fmt.Println(tc)
td, _ := tensor.Sub(ta, tb)
fmt.Println("\ntensor a-b:")
fmt.Println(td)
// add in-place
tensor.Add(ta, tb, tensor.UseUnsafe())
fmt.Println("\ntensor a+b(in-place):")
fmt.Println(ta)
// tensor add scalar
tg, err := tensor.Add(tb, float32(3.14))
if err != nil {
fmt.Println("add scalar error:", err)
return
}
fmt.Println("\ntensor b+3.14:")
fmt.Println(tg)
// add two tensors of different shape
te := tensor.New(tensor.WithBacking([]float32{1.7, 2.6, 1.3,
3.2, 2.7, 2.8}), tensor.WithShape(2, 3))
fmt.Println("\ntensor e:")
fmt.Println(te)
tf, err := tensor.Add(ta, te)
fmt.Println("\ntensor a+e:")
if err != nil {
fmt.Println("add error:", err)
return
}
fmt.Println(tf)
}運行該示例:
$ASSUME_NO_MOVING_GC_UNSAFE_RISK_IT_WITH=go1.20 go run tensor_add_sub.go
tensor a:
?1.7 2.6 1.3 3.2?
?2.7 2.8 1.5 2.9?
?3.7 2.4 1.7 3.1?
tensor b:
?1.7 2.6 1.3 3.2?
?2.7 2.8 1.5 2.9?
?3.7 2.4 1.7 3.1?
tensor a+b:
?3.4 5.2 2.6 6.4?
?5.4 5.6 3 5.8?
?7.4 4.8 3.4 6.2?
tensor a-b:
?0 0 0 0?
?0 0 0 0?
?0 0 0 0?
tensor a+b(in-place):
?3.4 5.2 2.6 6.4?
?5.4 5.6 3 5.8?
?7.4 4.8 3.4 6.2?
tensor b+3.14:
? 4.84 5.74 4.44 6.34?
? 5.84 5.94 4.6400003 6.04?
? 6.84 5.54 4.84 6.24?
tensor e:
?1.7 2.6 1.3?
?3.2 2.7 2.8?
tensor a+e:
add error: Add failed: Shape mismatch. Expected (2, 3). Got (3, 4)我們看到:tensor加減法是一個逐元素(element-wise)進行的操作,要求參與張量運算的張量必須有相同的shape,同位置的兩個元素相加,否則會像示例中最后的a+e那樣報錯;tensor加法支持tensor與一個scalar(標量)進行加減,原理就是tensor中每個元素都與這個標量相加減;此外若傳入tensor.Unsafe這個option后,參與加減法操作的第一個tensor的值會被結果重寫掉(override)。
3.2. 乘法和除法
兩個張量的相乘或相除是機器學習算法中另一個常見的操作。在Go中,我們可以使用Gorgonia/tensor提供的Mul和Div函數進行乘除運算。下面是一個使用Gorgonia/tensor進行乘法和除法運算的示例代碼:
// https://github.com/bigwhite/experiments/blob/master/go-and-nn/tensor-operations/tensor_mul_div.go
func main() {
// define two two-rank tensor
ta := tensor.New(tensor.WithBacking([]float32{1.7, 2.6, 1.3, 3.2,
2.7, 2.8, 1.5, 2.9,
3.7, 2.4, 1.7, 3.1}), tensor.WithShape(3, 4))
fmt.Println("\ntensor a:")
fmt.Println(ta)
tb := tensor.New(tensor.WithBacking([]float32{1.7, 2.6, 1.3, 3.2,
2.7, 2.8, 1.5, 2.9,
3.7, 2.4, 1.7, 3.1}), tensor.WithShape(3, 4))
fmt.Println("\ntensor b:")
fmt.Println(tb)
tc, err := tensor.Mul(ta, tb)
if err != nil {
fmt.Println("multiply error:", err)
return
}
fmt.Println("\ntensor a x b:")
fmt.Println(tc)
// multiple tensor and a scalar
td, err := tensor.Mul(ta, float32(3.14))
if err != nil {
fmt.Println("multiply error:", err)
return
}
fmt.Println("\ntensor ta x 3.14:")
fmt.Println(td)
// divide two tensors
td, err = tensor.Div(ta, tb)
if err != nil {
fmt.Println("divide error:", err)
return
}
fmt.Println("\ntensor ta / tb:")
fmt.Println(td)
// multiply two tensors of different shape
te := tensor.New(tensor.WithBacking([]float32{1.7, 2.6, 1.3,
3.2, 2.7, 2.8}), tensor.WithShape(2, 3))
fmt.Println("\ntensor e:")
fmt.Println(te)
tf, err := tensor.Mul(ta, te)
fmt.Println("\ntensor a x e:")
if err != nil {
fmt.Println("mul error:", err)
return
}
fmt.Println(tf)
}運行該示例,我們可以看到如下結果:
$ASSUME_NO_MOVING_GC_UNSAFE_RISK_IT_WITH=go1.20 go run tensor_mul_div.go
tensor a:
?1.7 2.6 1.3 3.2?
?2.7 2.8 1.5 2.9?
?3.7 2.4 1.7 3.1?
tensor b:
?1.7 2.6 1.3 3.2?
?2.7 2.8 1.5 2.9?
?3.7 2.4 1.7 3.1?
tensor a x b:
? 2.89 6.7599993 1.6899998 10.240001?
?7.2900004 7.8399997 2.25 8.410001?
?13.690001 5.76 2.89 9.61?
tensor ta x 3.14:
?5.3380003 8.164 4.082 10.048?
? 8.478001 8.792 4.71 9.106001?
?11.618001 7.5360007 5.3380003 9.734?
tensor ta / tb:
?1 1 1 1?
?1 1 1 1?
?1 1 1 1?
tensor e:
?1.7 2.6 1.3?
?3.2 2.7 2.8?
tensor a x e:
mul error: Mul failed: Shape mismatch. Expected (2, 3). Got (3, 4)我們看到,和加減法一樣,tensor的乘除法也是逐元素進行的,同時也支持與scalar的乘除。但對于shape不同的兩個tensor,Mul和Div會報錯。
了解了加減、乘除等基本操作后,下面我們再探索一寫更高級的張量操作。
4. Go中的高級張量操作
除了基本的張量操作外,Go還提供了一些高級的張量操作,用于復雜的機器學習算法中。讓我們來探討一下Go中的一些高級張量操作。
4.1. 點積
點積運算,也叫張量積(tensor product,不要與上面的逐元素的乘積弄混),是線性代數和機器學習算法中的一個作最常見也最有用的張量運算。與逐元素的運算不同,它將輸入張量的元素合并在一起。
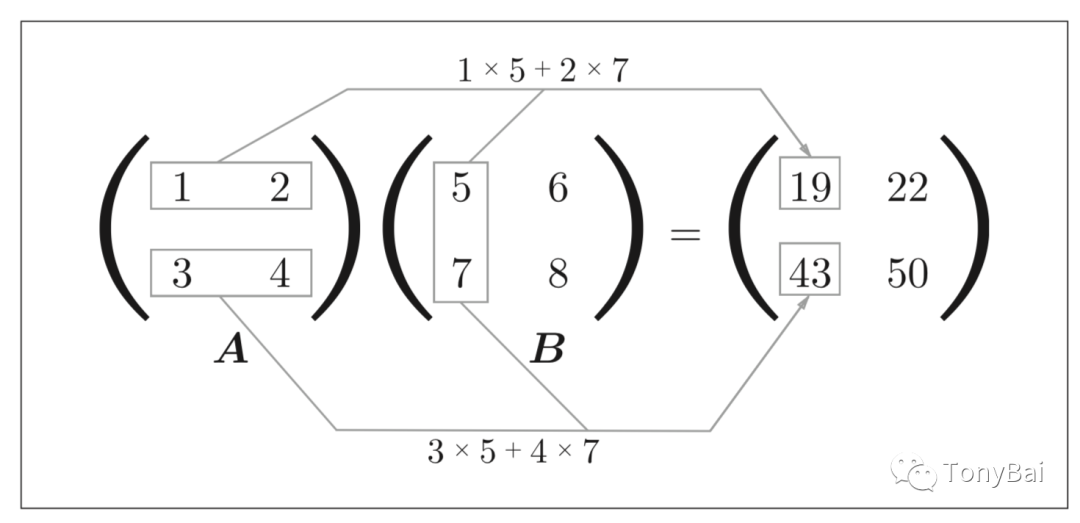
它涉及到將兩個張量元素相乘,然后將結果相加。這里借用魚書中的圖來直觀的看一下二階tensor計算過程:
 圖片
圖片
圖中是兩個shape為(2, 2)的tensor的點積。
下面是更一般的兩個二階tensor t1和t2:
tensor t1: shape(a, b)
tensor t2: shape(c, d)t1和t2可以做點積的前提是b == c,即第一個tensor t1的shape[1] == 第二個tensor t2的shape[0]。
在Go中,我們可以Dot函數來實現點積操作。下面是使用Gorgonia/tensor進行點積操作的例子:
// https://github.com/bigwhite/experiments/blob/master/go-and-nn/tensor-operations/tensor_dot.go
func main() {
// define two two-rank tensor
ta := tensor.New(tensor.WithBacking([]float32{1, 2, 3, 4}), tensor.WithShape(2, 2))
fmt.Println("\ntensor a:")
fmt.Println(ta)
tb := tensor.New(tensor.WithBacking([]float32{5, 6, 7, 8}), tensor.WithShape(2, 2))
fmt.Println("\ntensor b:")
fmt.Println(tb)
tc, err := tensor.Dot(ta, tb)
if err != nil {
fmt.Println("dot error:", err)
return
}
fmt.Println("\ntensor a dot b:")
fmt.Println(tc)
td := tensor.New(tensor.WithBacking([]float32{5, 6, 7, 8, 9, 10}), tensor.WithShape(2, 3))
fmt.Println("\ntensor d:")
fmt.Println(td)
te, err := tensor.Dot(ta, td)
if err != nil {
fmt.Println("dot error:", err)
return
}
fmt.Println("\ntensor a dot d:")
fmt.Println(te)
// three-rank tensor dot two-rank tensor
tf := tensor.New(tensor.WithBacking([]float32{23: 12}), tensor.WithShape(2, 3, 4))
fmt.Println("\ntensor f:")
fmt.Println(tf)
tg := tensor.New(tensor.WithBacking([]float32{11: 12}), tensor.WithShape(4, 3))
fmt.Println("\ntensor g:")
fmt.Println(tg)
th, err := tensor.Dot(tf, tg)
if err != nil {
fmt.Println("dot error:", err)
return
}
fmt.Println("\ntensor f dot g:")
fmt.Println(th)
}運行該示例,我們可以看到如下結果:
$ASSUME_NO_MOVING_GC_UNSAFE_RISK_IT_WITH=go1.20 go run tensor_dot.go
tensor a:
?1 2?
?3 4?
tensor b:
?5 6?
?7 8?
tensor a dot b:
?19 22?
?43 50?
tensor d:
? 5 6 7?
? 8 9 10?
tensor a dot d:
?21 24 27?
?47 54 61?
tensor f:
? 0 0 0 0?
? 0 0 0 0?
? 0 0 0 0?
? 0 0 0 0?
? 0 0 0 0?
? 0 0 0 12?
tensor g:
? 0 0 0?
? 0 0 0?
? 0 0 0?
? 0 0 12?
tensor f dot g:
? 0 0 0?
? 0 0 0?
? 0 0 0?
? 0 0 0?
? 0 0 0?
? 0 0 144?我們看到大于2階的高階tensor也可以做點積,只要其形狀匹配遵循與前面2階張量相同的原則:
(a, b, c, d) . (d,) -> (a, b, c)
(a, b, c, d) . (d, e) -> (a, b, c, e)4.2. 轉置
轉置張量包括翻轉其行和列。這是機器學習算法中的一個常見操作,廣泛應用在圖像處理和自然語言處理等領域。在Go中,我們可以使用tensor包提供的Transpose函數對tensor進行轉置:
// https://github.com/bigwhite/experiments/blob/master/go-and-nn/tensor-operations/tensor_transpose.go
func main() {
// define two-rank tensor
ta := tensor.New(tensor.WithBacking([]float32{1, 2, 3, 4, 5, 6}), tensor.WithShape(3, 2))
fmt.Println("\ntensor a:")
fmt.Println(ta)
tb, err := tensor.Transpose(ta)
if err != nil {
fmt.Println("transpose error:", err)
return
}
fmt.Println("\ntensor a transpose:")
fmt.Println(tb)
// define three-rank tensor
tc := tensor.New(tensor.WithBacking([]float32{1, 2, 3, 4, 5, 6,
7, 8, 9, 10, 11, 12,
13, 14, 15, 16, 17, 18,
19, 20, 21, 22, 23, 24}), tensor.WithShape(2, 3, 4))
fmt.Println("\ntensor c:")
fmt.Println(tc)
fmt.Println("tc shape:", tc.Shape())
td, err := tensor.Transpose(tc)
if err != nil {
fmt.Println("transpose error:", err)
return
}
fmt.Println("\ntensor c transpose:")
fmt.Println(td)
fmt.Println("td shape:", td.Shape())
}運行上面示例:
$ASSUME_NO_MOVING_GC_UNSAFE_RISK_IT_WITH=go1.20 go run tensor_transpose.go
tensor a:
?1 2?
?3 4?
?5 6?
tensor a transpose:
?1 3 5?
?2 4 6?
tensor c:
? 1 2 3 4?
? 5 6 7 8?
? 9 10 11 12?
?13 14 15 16?
?17 18 19 20?
?21 22 23 24?
tc shape: (2, 3, 4)
tensor c transpose:
? 1 13?
? 5 17?
? 9 21?
? 2 14?
? 6 18?
?10 22?
? 3 15?
? 7 19?
?11 23?
? 4 16?
? 8 20?
?12 24?
td shape: (4, 3, 2)接下來,我們再來探討兩個張量的高級操作:重塑(也叫變形)與廣播。
5. 在Go中重塑與廣播張量
在機器學習算法中,經常需要對張量進行重塑和廣播,使其與不同的操作兼容。Go提供了幾個函數來重塑和廣播張量。讓我們來探討如何在Go中重塑和廣播張量。
5.1. 重塑張量
重塑一個張量涉及到改變它的尺寸到一個新的形狀。在Go中,我們可以使用Gorgonia/tensor提供的Dense類型的Reshape方法來重塑張量自身。
下面是一個使用Gorgonia重塑張量的示例代碼:
// https://github.com/bigwhite/experiments/blob/master/go-and-nn/tensor-operations/tensor_reshape.go
func main() {
// define two-rank tensor
ta := tensor.New(tensor.WithBacking([]float32{1, 2, 3, 4, 5, 6}), tensor.WithShape(3, 2))
fmt.Println("\ntensor a:")
fmt.Println(ta)
fmt.Println("ta shape:", ta.Shape())
err := ta.Reshape(2, 3)
if err != nil {
fmt.Println("reshape error:", err)
return
}
fmt.Println("\ntensor a reshape(2,3):")
fmt.Println(ta)
fmt.Println("ta shape:", ta.Shape())
err = ta.Reshape(1, 6)
if err != nil {
fmt.Println("reshape error:", err)
return
}
fmt.Println("\ntensor a reshape(1, 6):")
fmt.Println(ta)
fmt.Println("ta shape:", ta.Shape())
err = ta.Reshape(2, 1, 3)
if err != nil {
fmt.Println("reshape error:", err)
return
}
fmt.Println("\ntensor a reshape(2, 1, 3):")
fmt.Println(ta)
fmt.Println("ta shape:", ta.Shape())
}運行上述代碼,我們將看到:
$ASSUME_NO_MOVING_GC_UNSAFE_RISK_IT_WITH=go1.20 go run tensor_reshape.go
tensor a:
?1 2?
?3 4?
?5 6?
ta shape: (3, 2)
tensor a reshape(2,3):
?1 2 3?
?4 5 6?
ta shape: (2, 3)
tensor a reshape(1, 6):
R[1 2 3 4 5 6]
ta shape: (1, 6)
tensor a reshape(2, 1, 3):
?1 2 3?
?4 5 6?
ta shape: (2, 1, 3)由此看來,張量轉置其實是張量重塑的一個特例,只是將將軸對調。
5.2. 廣播張量
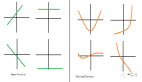
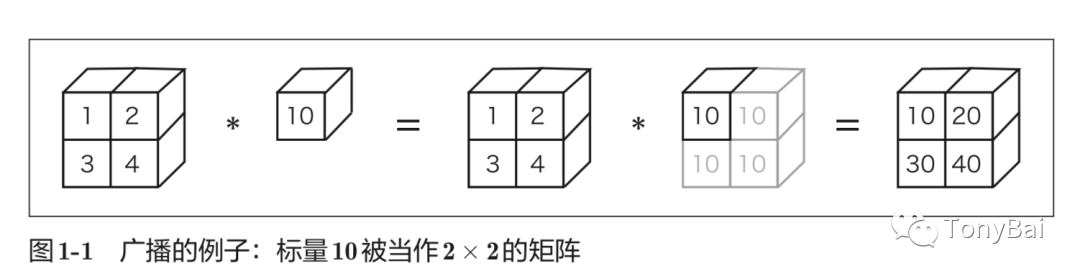
廣播張量涉及到擴展其維度以使其與其他操作兼容。下面是魚書中關于廣播(broadcast)的圖解:
 圖片
圖片
我們看到圖中這個標量(Scalar)擴展維度后與第一個張量做乘法操作,與我們前面說到的張量與標量(scalar)相乘是一樣的。如上圖中這種標量10被擴展成了2 × 2的形狀后再與矩陣A進行乘法運算,這個的功能就稱為廣播(broadcast)。
在魚書中還提到了“借助這個廣播功能,不同形狀的張量之間也可以順利地進行運算”以及下面圖中這個示例:
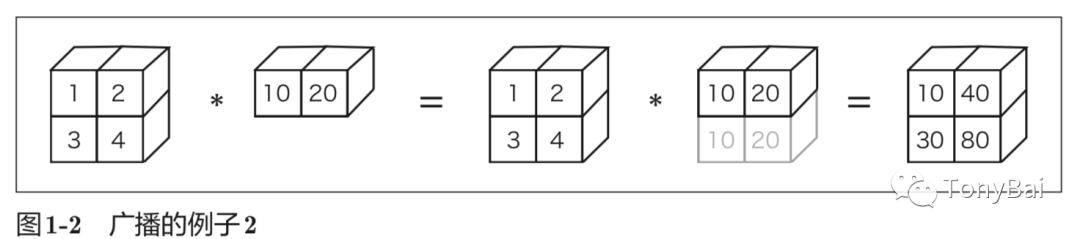
但Gorgonia/tensor包目前并不支持除標量之外的“廣播”。
6. 小結
張量操作在機器學習和數據科學中是必不可少的,它允許我們有效地操縱多維數組。在這篇文章中,我們探討了如何使用Go創建和執行基本和高級張量操作。我們還學習了廣播和重塑張量,使它們與不同的機器學習模型兼容。
我希望這篇文章能為后續繼續探究深度學習與神經網絡奠定一個基礎,讓你開始探索Go中的張量操作,并使用它們來解決現實世界的問題。
注:說實話,Go在機器學習領域的應用并不廣泛,前景也不明朗,零星的幾個開源庫似乎也不是很活躍。這里也僅是基于Go去學習理解機器學習的概念和操作,真正為生產編寫和訓練的機器學習模型與程序還是要使用Python。
本文涉及的源碼可以在這里[8]下載 - https://github.com/bigwhite/experiments/blob/master/go-and-nn/tensor-operations
7. 參考資料
- 《Python深度學習(第二版)》[9] - https://book.douban.com/subject/36078304/
- 魚書《深度學習入門:基于Python的理論與實現》[10] - https://book.douban.com/subject/30270959/
- 蘋果書《深入淺出神經網絡與深度學習》[11] - https://book.douban.com/subject/35128111/
- 《機器學習:Go語言實現》[12] - https://book.douban.com/subject/30457083/