本文作者曾秋皓，加拿大西安大略大學(xué)計算機(jī)系博士研究生，本科畢業(yè)于哈爾濱工業(yè)大學(xué)，碩士畢業(yè)于新加坡國立大學(xué)。在王博予教授和凌曉峰院士的指導(dǎo)下，博士期間主要圍繞隨時間變化的分布的問題展開理論、方法和應(yīng)用的研究。目前已在 ICLR/AAAI/IEEE TNNLS 發(fā)表多篇學(xué)術(shù)論文。

個人主頁：https://hardworkingpearl.github.io/

在現(xiàn)實世界的機(jī)器學(xué)習(xí)應(yīng)用中，隨時間變化的分布偏移是常見的問題。這種情況被構(gòu)建為時變域泛化（EDG），目標(biāo)是通過學(xué)習(xí)跨領(lǐng)域的潛在演變模式，并利用這些模式，使模型能夠在時間變化系統(tǒng)中對未見目標(biāo)域進(jìn)行良好的泛化。然而，由于 EDG 數(shù)據(jù)集中時間戳的數(shù)量有限，現(xiàn)有方法在捕獲演變動態(tài)和避免對稀疏時間戳的過擬合方面遇到了挑戰(zhàn)，這限制了它們對新任務(wù)的泛化和適應(yīng)性。

為了解決這個問題，我們提出了一種新的方法 SDE-EDG，它通過連續(xù)插值樣本收集數(shù)據(jù)分布的無限細(xì)分網(wǎng)格演變軌跡（IFGET），以克服過擬合的問題。此外，通過利用隨機(jī)微分方程（SDEs）捕獲連續(xù)軌跡的固有能力，我們提出了將 SDE 建模的軌跡通過最大似然估計與 IFGET 的軌跡對齊，從而實現(xiàn)捕獲分布演變趨勢。

• 論文標(biāo)題：Latent Trajectory Learning for Limited Timestamps under Distribution Shift over Time
• 論文鏈接：https://openreview.net/pdf?id=bTMMNT7IdW
• 項目鏈接：https://github.com/HardworkingPearl/SDE-EDG-iclr2024

方法

核心思想

為了克服這一挑戰(zhàn)，SDE-EDG 提出了一種新穎的方法，通過構(gòu)建無限細(xì)分網(wǎng)格演變軌跡（Infinitely Fined-Grid Evolving Trajectory, IFGET），在潛在表示空間中創(chuàng)建連續(xù)插值樣本，以彌合時間戳之間的間隔。此外，SDE-EDG 利用隨機(jī)微分方程（Stochastic Differential Equations, SDEs）的內(nèi)在能力來捕捉連續(xù)的軌跡動態(tài)，通過路徑對齊正則化器將 SDE 建模的軌跡與 IFGET 對齊，從而實現(xiàn)跨域捕獲演變分布趨勢。

方法細(xì)節(jié)

1. 構(gòu)建 IFGET：

首先，SDE-EDG 在潛在表示空間中為每個樣本建立樣本到樣本的對應(yīng)關(guān)系，收集每個個體樣本的演變軌跡。對于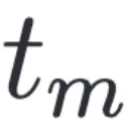時刻的每個類別 k 的任一樣本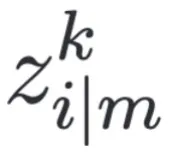，我們搜索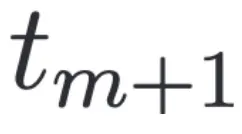時刻在特征空間離其最近的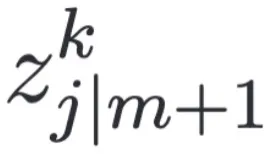為其在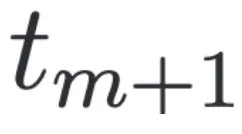的對應(yīng)樣本：

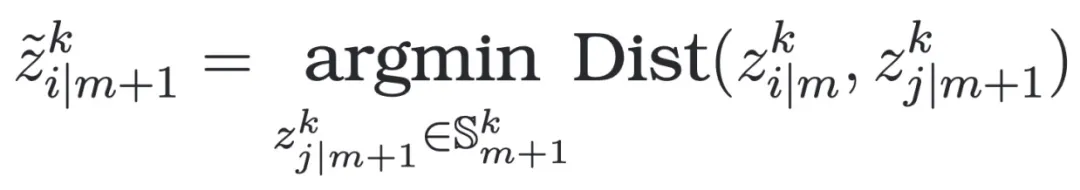
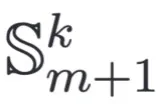這里是計算兩個向量之間的距離，是從下個領(lǐng)域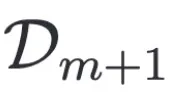采樣的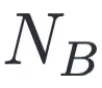個樣本的集合。

然后，利用這種對應(yīng)關(guān)系生成連續(xù)插值樣本，旨在連接時間戳間隔之間的時間間隙，避免對稀疏時間戳的過擬合，

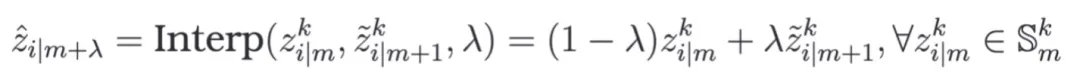
這里采樣自 Beta 分布。通過收集通過以上方式產(chǎn)生的樣本的時序軌跡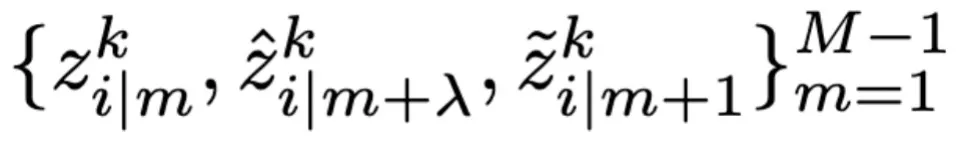，我們得到 IFGET。

2. 使用 SDE 建模軌跡：

SDE-EDG 采用神經(jīng) SDE 來模擬數(shù)據(jù)在潛在空間中的連續(xù)時間軌跡。與傳統(tǒng)的基于離散時間戳的模型不同， SDE 天然適合于模擬連續(xù)的時間軌跡。SDE-EDG 建模了時序軌跡，可以通過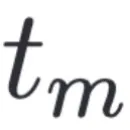時刻的樣本預(yù)測任意未來時刻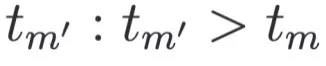的樣本：

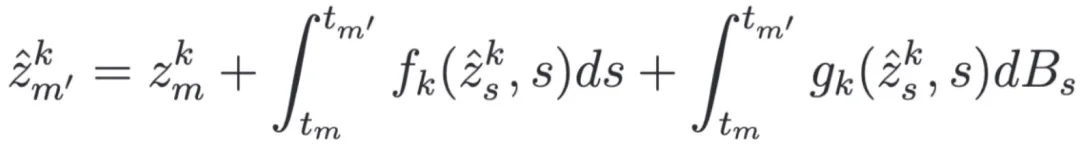
這里特征空間變量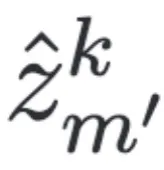是由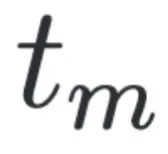時刻的樣本預(yù)測得到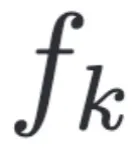，是 drift function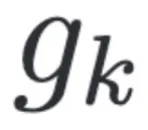，是 diffusion function。

3. 路徑對齊與最大似然估計：

SDE-EDG 通過最大化 IFGET 的似然估計來訓(xùn)練模型，

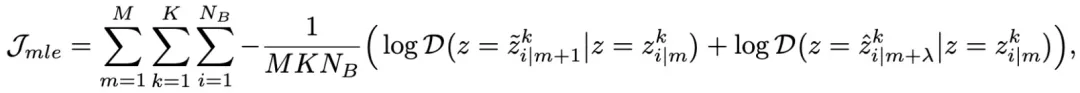
最終訓(xùn)練函數(shù)是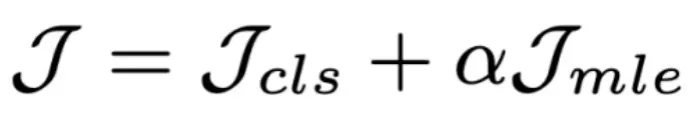，第一項是預(yù)測分類任務(wù)誤差損失函數(shù)。

4. 實驗

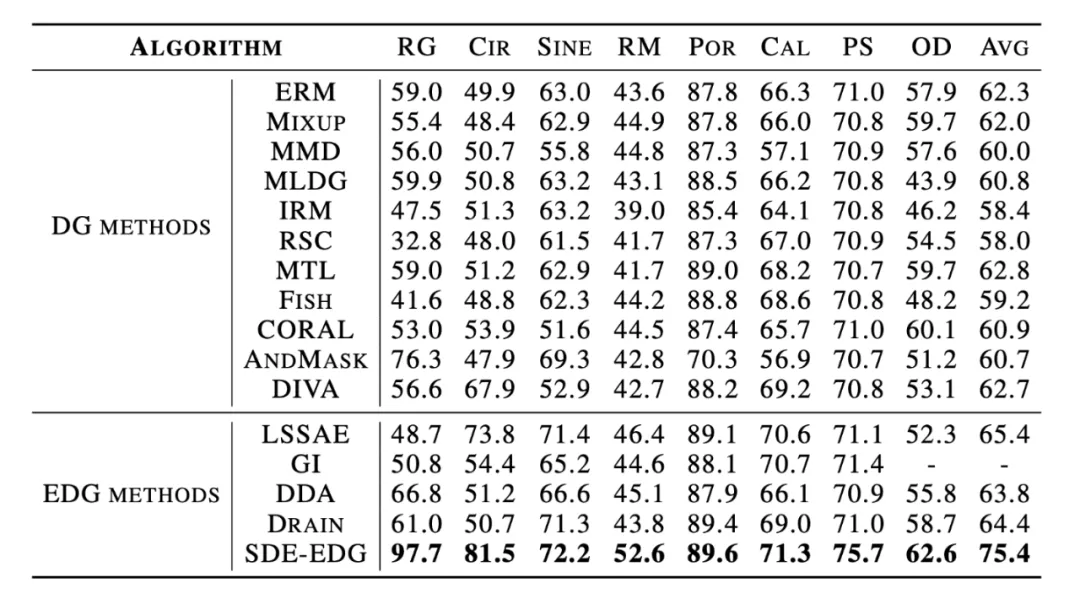
• 下表展示了 SDE-EDG 與其他基線方法在多個數(shù)據(jù)集上分類準(zhǔn)確率的比較。這些數(shù)據(jù)集包括 Rotated Gaussian (RG), Circle (Cir), Rotated MNIST (RM), Portraits (Por), Caltran (Cal), PowerSupply (PS), 和 Ocular Disease (OD)。結(jié)果顯示，SDE-EDG 在所有數(shù)據(jù)集上的平均準(zhǔn)確率均優(yōu)于其他方法。

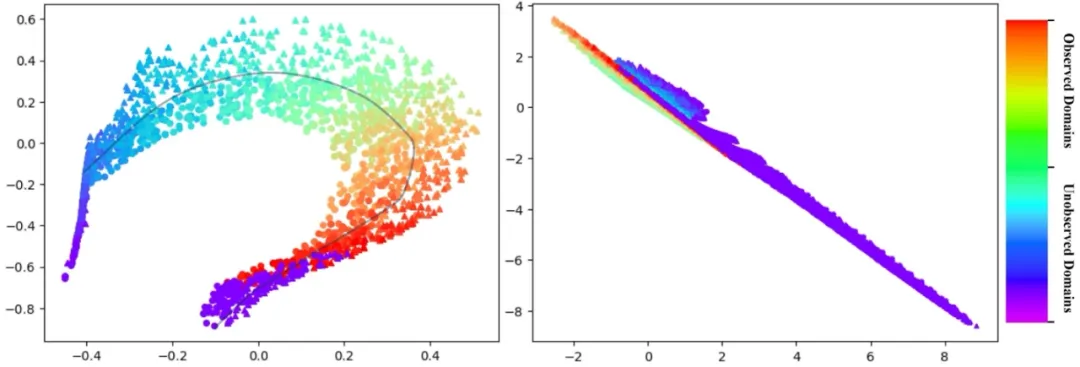
• 下圖提供了一個直觀的比較，展示了 SDE-EDG 算法（左）與傳統(tǒng) DG 方法 IRM（右）在特征表示方面的差異。通過數(shù)據(jù)特征空間的可視化，我們可以觀察到 SDE-EDG 學(xué)習(xí)到的特征表示具有明顯的決策邊界，其中不同類別的數(shù)據(jù)點被清晰地區(qū)分開來，以不同形狀表示，并且不同域的數(shù)據(jù)以彩虹條的顏色區(qū)分。這表明 SDE-EDG 能夠成功捕捉數(shù)據(jù)隨時間演變的動態(tài)，并在特征空間中保持類別的可分性。相比之下，IRM 的特征表示則傾向于將數(shù)據(jù)點坍縮到單一方向，導(dǎo)致決策邊界不明顯，這反映出 IRM 在捕捉時變分布趨勢方面的不足。

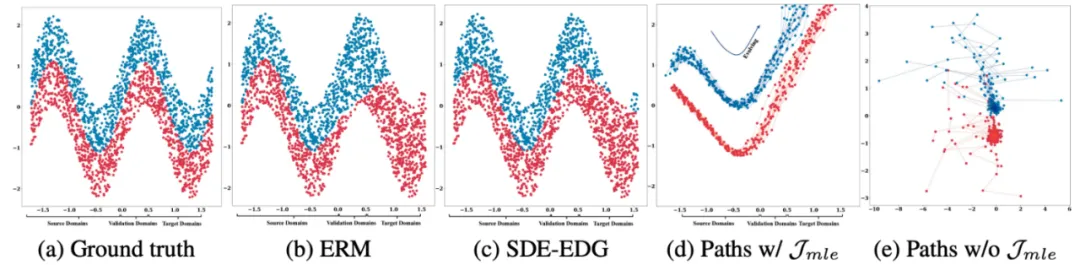
• 下圖通過一系列子圖深入展示了 SDE-EDG 算法在捕捉數(shù)據(jù)隨時間演變的能力方面的優(yōu)勢。子圖 (a) 提供了 Sine 數(shù)據(jù)集的真實標(biāo)簽分布，其中正例和負(fù)例用不同顏色的點表示，為后續(xù)的比較提供了基準(zhǔn)。接著，子圖 (b) 和 (c) 分別展示了基于 ERM 的傳統(tǒng)方法和 SDE-EDG 算法對同一數(shù)據(jù)集的預(yù)測結(jié)果，通過對比可以看出 SDE-EDG 在捕捉數(shù)據(jù)演變模式上的明顯優(yōu)勢。子圖 (d) 和 (e) 進(jìn)一步揭示了 SDE-EDG 學(xué)習(xí)到的演變路徑，其中 (d) 展示了應(yīng)用了路徑對齊損失（最大似然損失函數(shù)）后的路徑，而 (e) 展示了未應(yīng)用該損失時的路徑。通過這一對比，可以直觀地看到路徑對齊損失對于確保模型能夠正確捕捉和表征數(shù)據(jù)隨時間變化的重要性。

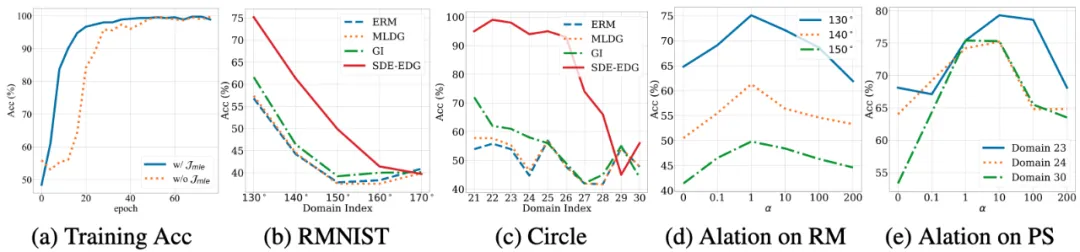
• 下圖子圖 (a) 展示了在 Portraits 數(shù)據(jù)集上，使用不同算法進(jìn)行訓(xùn)練時的準(zhǔn)確率收斂軌跡。這個子圖提供了一個直觀的視角，用以比較 SDE-EDG 算法與其他基線方法（如 ERM、MLDG、GI）在訓(xùn)練過程中性能的變化情況。通過觀察訓(xùn)練準(zhǔn)確率隨時間推移的增長趨勢，我們可以評估不同算法的學(xué)習(xí)能力和收斂速度。SDE-EDG 算法的收斂軌跡尤其值得關(guān)注，因為它揭示了該算法在適應(yīng)不斷演變的數(shù)據(jù)分布時的效率和穩(wěn)定性。
  
  下圖子圖 (b) 和 (c) 分別展示了 RMNIST 和 Circle 數(shù)據(jù)集上，SDE-EDG 算法在這些數(shù)據(jù)集上的表現(xiàn)顯示出其在處理時變分布時的優(yōu)越性，即使在面對較大時間跨度的目標(biāo)域時，也能保持較高的準(zhǔn)確率，這表明了 SDE-EDG 算法在捕捉和適應(yīng)數(shù)據(jù)演變模式方面的強(qiáng)大能力。
  
  下圖子圖 (d) 和 (e) 探討了最大似然損失（Maximum Likelihood Loss）在 RMNIST 和 PowerSupply 數(shù)據(jù)集上對 SDE-EDG 性能的影響。通過改變正則化權(quán)重 α 的值，這兩個子圖展示了不同 α 設(shè)置對模型性能的具體影響。實驗結(jié)果表明，適當(dāng)?shù)?α 值可以顯著提高 SDE-EDG 在特定數(shù)據(jù)集上的性能，這強(qiáng)調(diào)了在實際應(yīng)用中根據(jù)數(shù)據(jù)集特性和任務(wù)需求調(diào)整超參數(shù)的重要性。

結(jié)論

論文作者提出了一種新的 SDE-EDG 方法，用于建模時變域泛化（EDG）問題。方法涉及通過識別樣本到樣本的對應(yīng)關(guān)系并生成連續(xù)插值樣本來構(gòu)建 IFGET。隨后，作者采用隨機(jī)微分方程（SDE）并將其與 IFGET 對齊進(jìn)行訓(xùn)練。文章的貢獻(xiàn)在于揭示了通過收集個體的時間軌跡來捕獲演變模式的重要性，以及在時間間隔之間進(jìn)行插值以減輕源時間戳數(shù)量有限的問題，這有效地防止了 SDE-EDG 對有限時間戳的過擬合。