“ 反向傳播是大模型訓練的核心，沒有反向傳播就沒有大模型”

了解過大模型技術的人應該都知道，大模型有幾個核心模塊；對應的也有幾個核心技術點，比如訓練數據的準備，機器學習(神經網絡)模型的設計，損失函數的設計，反向傳播算法等。

而今天討論的就是反向傳播算法，其可以說是模型訓練的核心模塊，沒有反向傳播模型訓練就無從談起。

那么，反向傳播算法是怎么實現的呢？其技術原理是什么？有哪些注意點？

反向傳播算法的實現

介紹

反向傳播是深度神經網絡訓練的核心算法，旨在通過計算和傳播梯度來優(yōu)化模型參數；以下是從原理，實現和技術細節(jié)等多個方面對反向傳播進行介紹。

原理

反向傳播算法的核心是鏈式法則，目的是通過計算損失函數對模型參數的梯度來優(yōu)化模型。具體來說：

鏈式法則：反向傳播利用鏈式法則將損失函數對模型輸出的梯度逐層傳播到網絡中的每個參數。鏈式法則的核心思想是：

如果一個函數 zz 是由兩個函數 ff 和 gg 組合而成，即 z=f(g(x))z=f(g(x))，那么 zz 對 xx 的導數可以表示為 dzdx=dzdg?dgdxdxdz=dgdz?dxdg

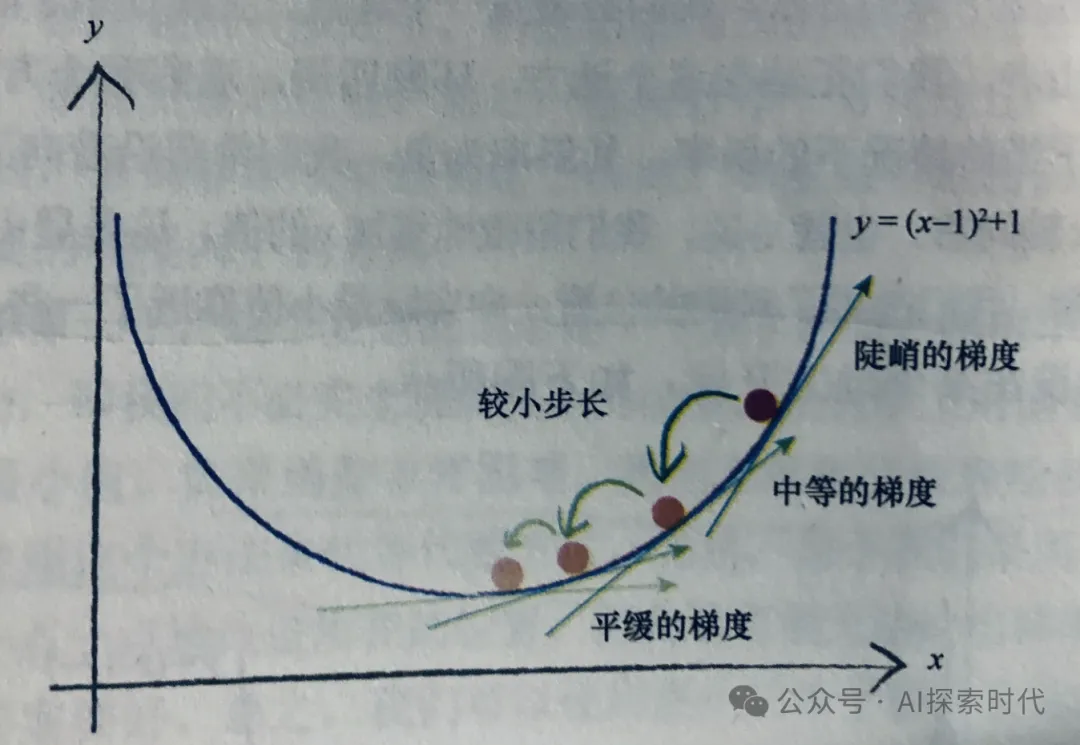
梯度下降：計算出的梯度用來調整模型參數，以減少損失函數值；參數更新的步驟通常是基于梯度下降算法

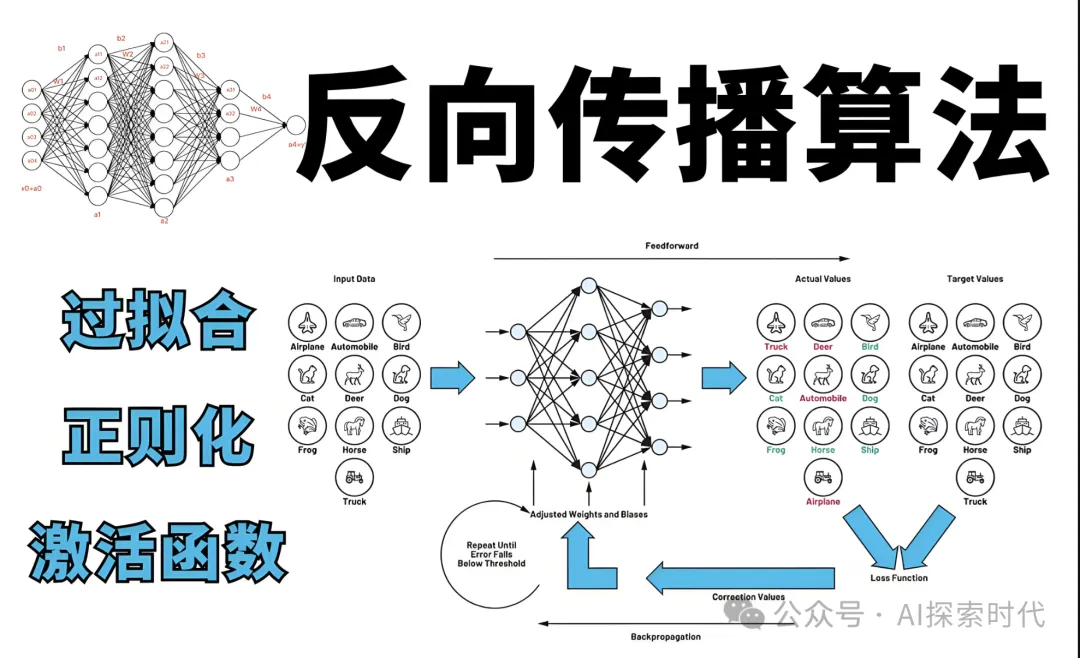
實現步驟

前向傳播

在反向傳播之前，首先要進行前向傳播以計算預測值和損失差：

輸入數據：將數據傳人網絡的輸入層

計算每層的輸出：

    對于沒一層計算加權和并加上偏執(zhí)

    應用激活函數得到該層的輸出

計算損失：用損失函數(如均方差，交叉熵等)計算預測值與實際標簽之間的差距

計算損失對輸出的梯度

損失函數對輸出的梯度：計算損失函數對網絡輸出的偏導數，這一過程取決于損失函數的類型

反向傳播梯度

輸出層到倒數第二層

計算輸出層的梯度(損失對輸出的梯度)，并通過鏈式法則計算每一層的梯度

對于每層 ll，計算：

• 激活函數的導數。
• 損失函數對每個神經元的梯度。
• 權重和偏置的梯度

從倒數第二層到第一層：

• 繼續(xù)向前一層傳播梯度。
• 更新每層的權重和偏置。

更新參數

使用計算得到的梯度來更新權重和偏置：

WL:=WL?η??L?WL

bL:=bL?η??L?bL

其中，η是學習率，?L?WL和 ?L?bL

技術細節(jié)

激活函數和其導數

常見激活函數：
Sigmoid：σ(x)=11+e?x


ReLU：ReLU(x)=max?(0,x)
Tanh：Tanh(x)=ex?e?xex+e?x


激活函數的導數：
Sigmoid：σ′(x)=σ(x)?(1?σ(x))


ReLU：ReLU′(x)={1 if x>00 if x≤0
Tanh：Tanh′(x)=1?Tanh2(x)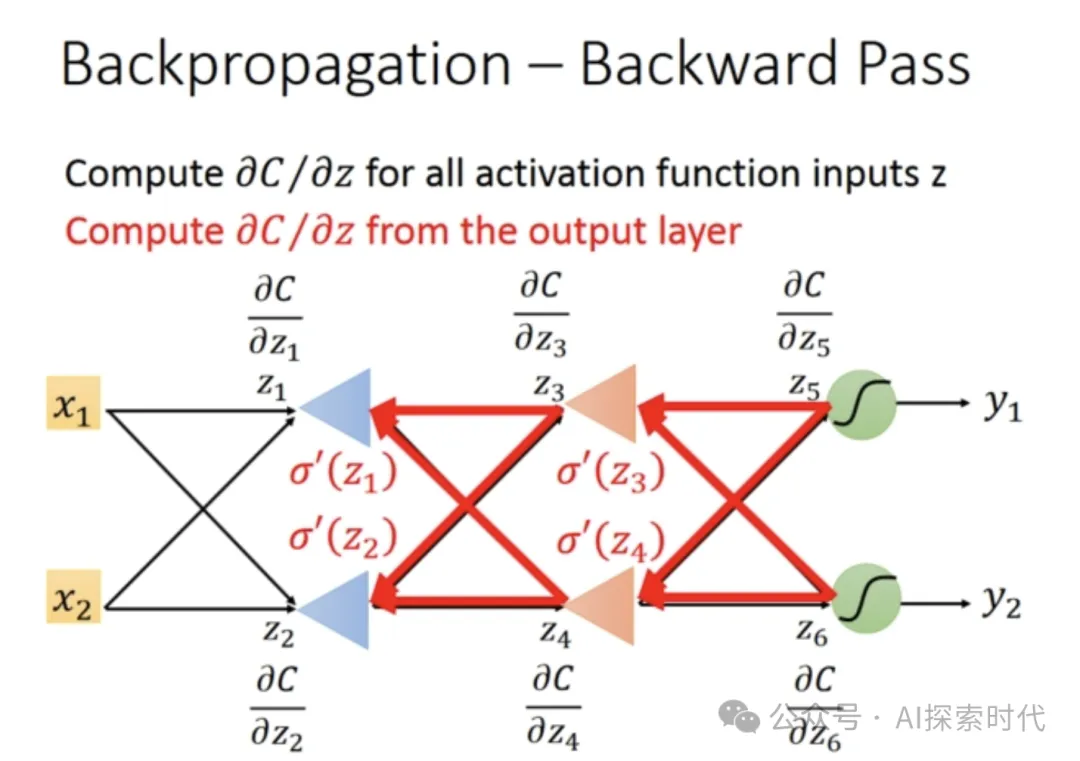

梯度計算

權重梯度：對于每個權重 WW，梯度為：

?W/?L=δ?Aprev

其中 δ是當前層的誤差項，aprev是前一層的激活值。

• 偏置梯度：對于每個偏置 bb，梯度為：

?L?b=δ

參數更新

學習率：決定了每次更新的步長，通常使用較小的學習率，以確保穩(wěn)定的收斂

優(yōu)化算法：除了標準的梯度下降，還可以使用動量，RMSprop、Adam 等優(yōu)化算法來提高訓練效率與效果

正則化

L1/L2正則化：通過在損失函數中加入權重的L1和L2范數來防止過擬合

Dropout：在訓練過程中隨機忽略一些神經元，以防止網絡對訓練數據的過擬合

數值穩(wěn)定性

梯度消失：在深層網絡中，梯度可能會變得非常小，導致學習過程緩慢或停滯。可以使用ReLU激活函數或歸一化技術(如批量歸一化)來緩解

梯度爆炸：梯度值變得非常大，可能導致訓練不穩(wěn)定，可以使用梯度裁剪來限制梯度大小

實際應用

框架支持：現代深度學習框架(如TensorFlow，PyTorch等)提供了自動微分功能，簡化了反向傳播的實現和梯度計算

并行計算：使用GPU加速前向傳播和反向傳播的計算，提高訓練效率

總結

反向傳播算法通過計算損失函數對網絡參數的梯度，利用鏈式法則將梯度從輸出層逐層傳播到輸入層，從而更新網絡的權重與偏執(zhí)；其核心在于計算梯度并利用優(yōu)化算法進行參數更新；掌握反向傳播的原理和技術細節(jié)對于訓練神經網絡非常重要。

本文轉載自公眾號AI探索時代 作者：DFires

原文鏈接：?????https://mp.weixin.qq.com/s/s8owdnwSZ4ggKiNfkCxDQg???