一、引言

現(xiàn)階段，程序代碼是解決基于大型語言模型（LLM）的復雜推理任務的有效的方式之一，這類方法通常被稱為"程序或代碼思維鏈" (program-of-thought)。與傳統(tǒng)思維鏈(chain-of-thought)方法相比，代碼思維鏈方法將復雜問題分解為可執(zhí)行的代碼片段，并且利用代碼執(zhí)行器逐步解決子問題，可以較大程度提升基于大型語言模型的推理能力。然而目前代碼程序數(shù)據(jù)本身的形式與大模型推理能力之間的相關(guān)性仍是未解之謎，我們對于構(gòu)造何種代碼指令數(shù)據(jù)才能提升基于代碼思維鏈的大模型推理能力仍知之甚少。因此，本文致力于分析以下問題：

什么情況下代碼思維鏈數(shù)據(jù)對語言模型推理最為有效？

本文分析了不同邏輯和結(jié)構(gòu)復雜度的代碼程序數(shù)據(jù)，初步探究了不同復雜度的代碼數(shù)據(jù)與語言模型推理能力的關(guān)系。

二、代碼程序復雜度估計

在這項工作中，我們提出Complexity-Impacted Reasoning Score (CIRS) 用來度量推理復雜度的分數(shù)。CIRS分數(shù)用于衡量代碼推理步驟（代碼思維鏈）對語言模型推理能力的影響。

我們假設代碼編程語言具有獨特的優(yōu)勢，原因如下：

• 首先，相較于扁平化的自然語言數(shù)據(jù)，得益于其面向?qū)ο蟮奶卣鳎a語言能夠更加有效建模復雜的結(jié)構(gòu)。
• 其次，程序語言具有相對固有的過程導向邏輯，其面向過程的特性有助于解決多步推理問題。

因此，合理的方式應該從結(jié)構(gòu)和邏輯兩個角度評估代碼的復雜性。

具體來說，為了衡量代碼思維鏈  的推理能力，我們定義為結(jié)構(gòu)復雜性  和邏輯復雜性  的乘積。

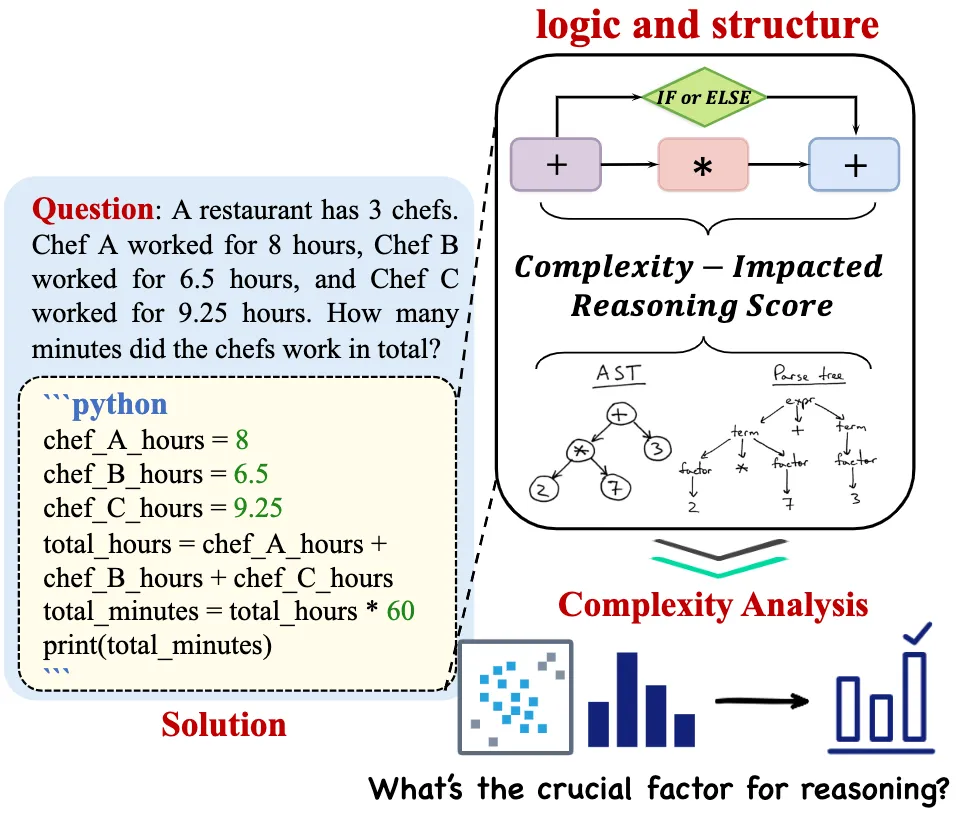
1.結(jié)構(gòu)復雜性定義

為了計算結(jié)構(gòu)復雜性，我們衡量抽象語法樹（AST）的結(jié)構(gòu)復雜性。具體來說，我們利用抽象語法樹中的三個指標來反映其結(jié)構(gòu)信息。

一般來說，節(jié)點數(shù)越多，復雜性越高。但是僅憑節(jié)點數(shù)無法全面衡量代碼的復雜性，因為一個具有簡單結(jié)構(gòu)的大代碼可能比一個具有復雜結(jié)構(gòu)的小代碼更容易理解。節(jié)點類型幫助識別代碼中存在的結(jié)構(gòu)元素，例如條件語句、循環(huán)和函數(shù)調(diào)用。不同的節(jié)點類型在代碼中扮演不同的角色，并對代碼的復雜性有不同的貢獻。因此，記錄各種節(jié)點類型的數(shù)量可以增進對代碼結(jié)構(gòu)復雜性的理解。最后，抽象語法樹 的深度反映了代碼中嵌套的級別。更大的樹深度可能意味著更復雜的控制流和邏輯，使代碼更難理解。同樣樹深度也不是唯一的衡量標準。一個具有多個簡單分支的淺樹可能比一個具有少數(shù)復雜分支的深樹更容易理解。

2.邏輯復雜性定義

受到 Halstead 復雜度 和 McCabe 的圈復雜度的啟發(fā)，我們定義代碼的邏輯復雜性 ，它包含了困難度和圈復雜度 。

其中表示代碼控制流圖中的邊數(shù)，表示代碼控制流圖中的節(jié)點數(shù)。高圈復雜度與潛在的程序錯誤之間存在顯著的相關(guān)性， 高圈復雜度的模塊和方法也會有最多的缺陷。我們注意到高圈復雜度表明程序代碼具有復雜的判斷邏輯，同時也可能導致較低的質(zhì)量，并且難以測試和維護。

總的來說，引入對于代碼塊困難度和圈復雜度的衡量指標，可以同時兼顧碼操作符、操作數(shù)和代碼控制流的復雜性對于代邏輯復雜度的影響。

三、實驗分析

本文的實驗分為兩部分，第一部分我們使用CIRS指標對代碼數(shù)據(jù)進行經(jīng)驗性分析，并且按照分數(shù)值進行劃分，最后探討不同復雜度代碼塊對大模型推理能力的影響。第二部分，我們將第一部分得到的結(jié)論用于代碼數(shù)據(jù)的過濾，篩選出對大模型推理能力增益最有效的代碼，在多個數(shù)據(jù)集上做驗證。

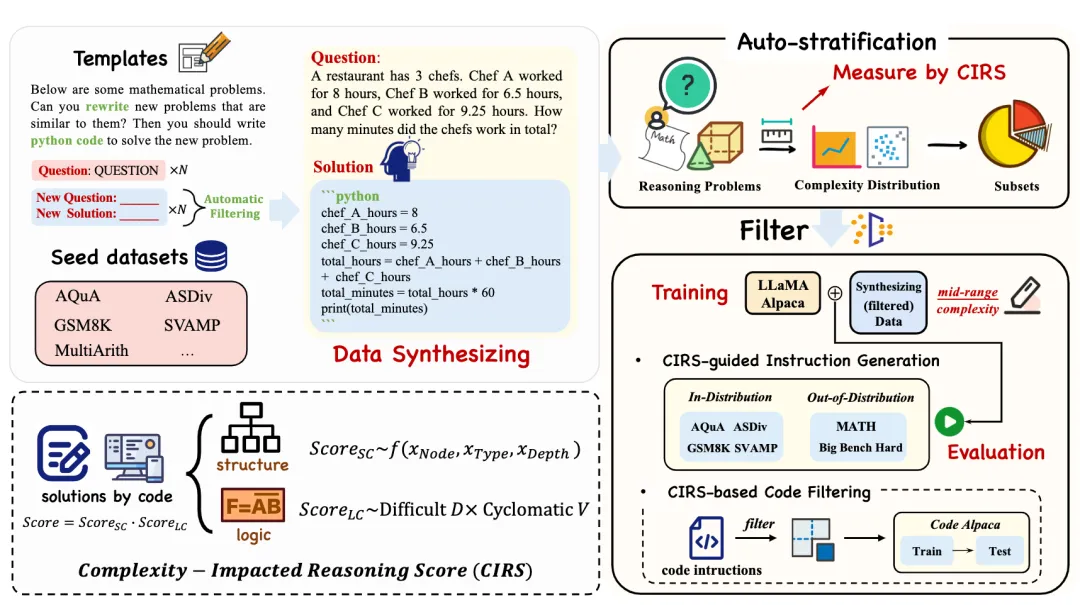
1.經(jīng)驗性實驗分析

為了盡量避免現(xiàn)有數(shù)據(jù)集本身造成的誤差，我們選擇模擬新的代碼數(shù)據(jù)，種子數(shù)據(jù)的來源包括GSM8K、MultiArith、Asdiv等訓練集。我們從五個種子數(shù)據(jù)集模擬合成了超過60,000個樣本。最后每個數(shù)據(jù)集生成了大約10,000個樣本，并且我們選擇盡可能多的數(shù)據(jù)集以確保數(shù)學問題的多樣性。在獲取到生成的代碼數(shù)據(jù)后，我們使用CIRS指標并根據(jù)代碼復雜性分布的分析手動將數(shù)據(jù)分成不同的子集。基于不同的復雜性分數(shù)，我們將劃分的子集命名為low（低分樣本）、medium（中分樣本）和high（高分樣本）。

（1）不同代碼程序復雜度分數(shù)的影響

合適代碼的復雜度對于代碼思維鏈的提示的推理能力至關(guān)重要：

從四個數(shù)據(jù)集的結(jié)果中，我們注意到當代碼數(shù)據(jù)的復雜性處于中等范圍時，模型的性能最佳。這表明學習性符號語言對于程序輔助提示的推理能力至關(guān)重要。其原因在于，過于簡單的復雜性數(shù)據(jù)對于大型語言模型（LLMs）來說太簡單，導致效果不太明顯。相反，當復雜性顯著增加時，邏輯語義和嵌套結(jié)構(gòu)變得難以理解或?qū)W習，這可能對大型語言模型的推理能力產(chǎn)生不利影響。

參數(shù)數(shù)量越大，代碼數(shù)據(jù)對于大型語言模型的推理能力提升越顯著：

隨著語言模型大小從70億增加到650億，其推理能力也在提高。實際上經(jīng)過微調(diào)后，大多數(shù)650億參數(shù)量的模型使用代碼數(shù)據(jù)可以達到與gpt-3.5-turbo相當?shù)慕Y(jié)果。這表明擁有足夠多的參數(shù)對于語言模型的實質(zhì)性推理能力至關(guān)重要。此外當語言模型足夠大時，不同復雜度代碼之間帶來的結(jié)果差異很小。這說明大量參數(shù)的語言模型能夠更加擅長處理符號數(shù)據(jù)，并且內(nèi)在的具有產(chǎn)生強大推理能力的潛力。

當前語言模型的架構(gòu)在理解推理能力方面存在局限性：

我們觀察到，當數(shù)據(jù)復雜性極高時，語言模型的性能傾向于下降，這反映了大型語言模型的推理能力有其固有的限制。首先，我們認為當前語言模型的架構(gòu)（例如decoder-only架構(gòu)）對于理解復雜知識的能力有限，這也限制了其推理能力的涌現(xiàn)。大模型展示強大推理能力的前提是它們能夠理解復雜數(shù)據(jù)中嵌入的結(jié)構(gòu)和邏輯知識。因此，未來的研究需要探索具有更強推理能力的模型基礎結(jié)構(gòu)。其次，進一步增強推理能力需要依賴外部工具。我們知道推理問題的范圍非常廣泛，不僅包括數(shù)學推理，還包括常識或更復雜的邏輯推理任務。因此，僅依靠LLM本身是不足以一次性解決所有問題的，需要更強大的外部工具的協(xié)助。

（2）不同復雜度分數(shù)的數(shù)據(jù)特征

不同CIRS分數(shù)的不同子集顯示出不同的結(jié)構(gòu)和邏輯差異，我們還發(fā)現(xiàn)不同復雜性分數(shù)的結(jié)果與推理問題的認知難度級別相對應。低分數(shù)的樣本包含很少的結(jié)構(gòu)信息。盡管它們包含一些中間推理過程，但這些主要以平面文本描述形式呈現(xiàn)。這些樣本通常對應于更簡單的、在結(jié)構(gòu)和邏輯上不足的問題。當分數(shù)在代碼推理步驟中增加時，具有簡單邏輯語義和結(jié)構(gòu)的編程語言的存在也隨之增加。這些樣本通常涉及簡單且直接的邏輯操作。得分極高的樣本包含大量的結(jié)構(gòu)化函數(shù)定義或推理過程，這表明存在許多復雜的條件語句和函數(shù)結(jié)構(gòu)。這些樣本通常是高度挑戰(zhàn)性的數(shù)學問題。

（3）排除數(shù)據(jù)分布本身的影響

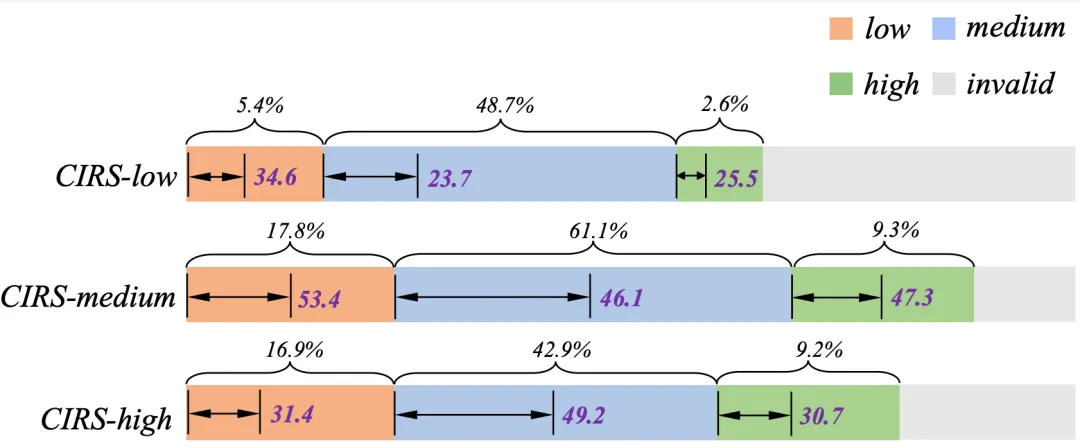
為了消除數(shù)據(jù)分布本身可能帶來的偏差，例如由于出現(xiàn)頻率較高而在中等數(shù)據(jù)范圍內(nèi)的性能提升，我們對不同復雜性分數(shù)的結(jié)果進行了更深入的分析。從實驗結(jié)果來看，模型對每種分布的預測準確率與訓練數(shù)據(jù)的數(shù)量無關(guān)。因此，我們可以初步得出結(jié)論，復雜性數(shù)據(jù)的有效性并非因為數(shù)據(jù)出現(xiàn)的頻率。

（4）代碼思維鏈和文本思維鏈的比較

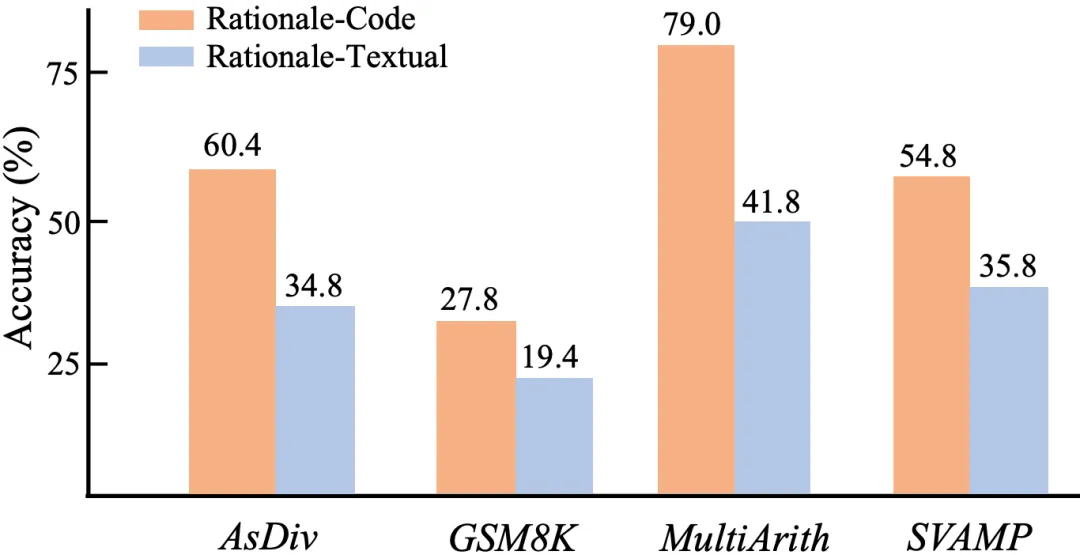
為了驗證代碼和文本推理鏈的效果，我們用文本替換了使用相同數(shù)據(jù)集的代碼程序推理過程。代碼數(shù)據(jù)集在所有四個數(shù)據(jù)集中都展示出明顯的優(yōu)勢。這是因為代碼本質(zhì)上包含了邏輯語義和結(jié)構(gòu)信息， 另一個原因是代碼可以被外部解釋器執(zhí)行。因此帶有代碼的提示方法優(yōu)于扁平化的文本信息。

2.使用CIRS提升大語言模型推理能力

（1）自動合成和劃分代碼數(shù)據(jù)算法

我們將第一部分實驗的步驟集成為一種自動合成和分層算法，然后將其應用于數(shù)學推理的指令生成任務，以及代碼生成任務中用來做代碼數(shù)據(jù)過濾。

（2）CIRS引導的指令生成

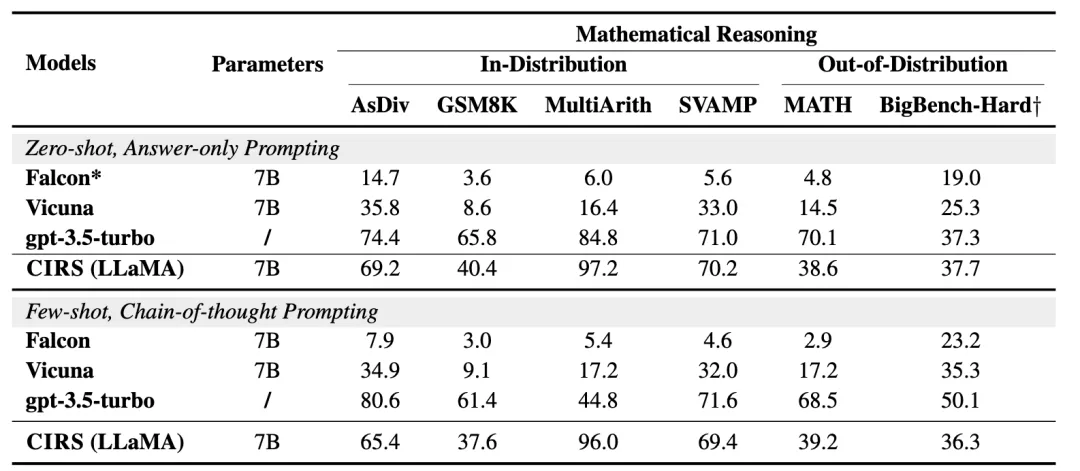
合適的代碼數(shù)據(jù)復雜性對于語言模型表現(xiàn)出最佳的推理能力更重要。因此，我們從源數(shù)據(jù)集中篩選出更多數(shù)據(jù)訓練一個針對中等復雜性范圍的代碼數(shù)據(jù)增強推理模型。在分布內(nèi)測試條件下，我們發(fā)現(xiàn)訓練的模型優(yōu)于Vicuna和Falcon。為了消除數(shù)據(jù)分布的影響，我們直接測試了模型在分布外設置中的性能。相同的參數(shù)下，我們的模型在零樣本和少樣本提示下表現(xiàn)更好。值得注意的是，我們的方法在零樣本設置下在BigBench-Hard與ChatGPT相當。對于MATH數(shù)據(jù)集，我們注意到我們的模型仍然優(yōu)于基線模型。但是由于代碼數(shù)據(jù)本身的局限性，我們的模型比ChatGPT差得多。

（3）不同推理復雜度分數(shù)的影響

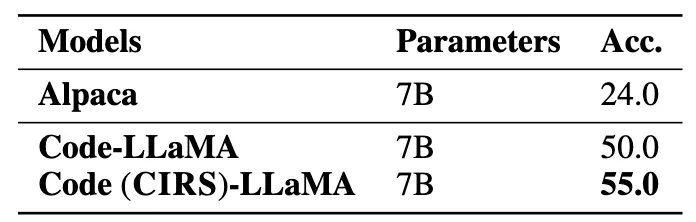
為了驗證我們方法在代碼相關(guān)任務中的有效性，我們過濾訓練數(shù)據(jù)集并獲得了更多高質(zhì)量代碼指令的子集。結(jié)果表明，Code (CIRS)-LLaMA在純代碼生成任務中表現(xiàn)出有效的性能。我們可以得出結(jié)論，優(yōu)化的結(jié)構(gòu)和邏輯語義對LLM的推理能力最有益。

四、討論與總結(jié)

1. 數(shù)學邏輯和代碼之間的深層聯(lián)系是什么?

柯里-霍華德同構(gòu)（Curry-Howard isomorphism）表明數(shù)學邏輯和計算機程序代碼之間的互為鏡像，同時這也說明了數(shù)學證明和計算機程序可以建立某種關(guān)聯(lián)，為我們理解語言模型也提供了啟發(fā)和思考。語言模型在處理代碼時，如果能夠理解和應用類型系統(tǒng)，就能更好地處理邏輯推理。類型系統(tǒng)在程序設計中用于約束和推理數(shù)據(jù)和函數(shù)之間的關(guān)系，類似于邏輯系統(tǒng)中命題和證明的關(guān)系。在編寫程序時，人需要對數(shù)據(jù)和操作進行邏輯推理。這與證明一個邏輯命題的過程有相似之處。語言模型如果能理解和生成程序代碼，就表明它在進行某種形式的邏輯推理。通過程序代碼的理解和生成，語言模型能夠更有效地進行邏輯推理，處理復雜的問題解決方案，這對于理解邏輯問題來解決特定問題是有用的。雖然柯里-霍華德同構(gòu)直接描述的是邏輯系統(tǒng)和類型系統(tǒng)之間的關(guān)系，但將這種理論應用于語言模型和程序代碼的融合，可以幫助模型更好地理解和處理邏輯推理和編程任務。這表明了邏輯學和計算機科學之間的深刻聯(lián)系也適用于人工智能和語言模型的領域。

2. 對于語言模型的推理能力來說，哪種數(shù)據(jù)格式至關(guān)重要？

在本文中，我們探討了程序思維提示鏈的推理能力。結(jié)果表明，具有某些邏輯和結(jié)構(gòu)特質(zhì)的優(yōu)化級別代碼數(shù)據(jù)是關(guān)鍵因素。代碼數(shù)據(jù)之所以高效，是因為它本質(zhì)上是半結(jié)構(gòu)化的，且在自然界中豐富存在。我們可以證明：(1) 數(shù)據(jù)的局部結(jié)構(gòu)特性對于提升推理能力至關(guān)重要，這與Prystawski等 (Why think step-by-step? Reasoning emerges from the locality of experience) 的觀點一致。數(shù)據(jù)中固有的邏輯連貫性或一定量的知識回路是必要的。(2) 過于復雜的結(jié)構(gòu)信息和邏輯對LLM來說是“太難學習”的。本文的實驗結(jié)果表明，最有效的是知識的最佳層次復雜度，因為它對大多數(shù)大型語言模型來說是可學習的。同時，我們還發(fā)現(xiàn)，隨著語言模型中參數(shù)數(shù)量的增加，它們對復雜知識的理解也在提高。

在本項工作中，我們致力于探究代碼思維鏈數(shù)據(jù)和大模型推理能力背后的機理，并提出CIRS來衡量代碼數(shù)據(jù)形式與大模型推理能力之間的關(guān)系。通過考慮代碼數(shù)據(jù)的結(jié)構(gòu)和邏輯屬性，我們使用AST來編碼結(jié)構(gòu)信息，并根據(jù)難度和圈復雜度編碼結(jié)構(gòu)特征。通過實證分析，我們發(fā)現(xiàn)代碼語言的合適水平在程序思維提示的推理能力中扮演著關(guān)鍵角色。進一步的，我們設計了應用數(shù)學推理和代碼生成任務的自動合成和分層算法。廣泛的結(jié)果證明了所提方法的有效性。在未來，我們將把這項工作擴展到更多場景，例如常識或邏輯推理任務，并以低計算成本訓練強大的推理模型。

本文轉(zhuǎn)載自：??ZJUKG??

作者：畢禎