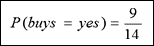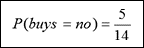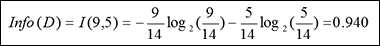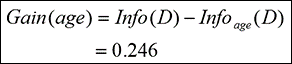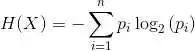如何創建完美的決策樹
譯文【51CTO.com快譯】眾所周知,決策樹在現實生活中有著許多實用的場景,它深刻地影響著包括分類和回歸在內的、非常廣泛的機器學習領域。可以說,在各種決策分析中,決策樹能夠起到直觀且明確的決策輔助性作用。
什么是決策樹?
決策樹是一系列相關選擇所產生的可能性結果的“展示圖”。它允許個人或組織根據其成本、概率和效益,來對各種可能采取的行動進行權衡。
顧名思義,決策樹使用的是樹狀的決策模型。它既可以被用于推進各種非正式的討論,又可以被用來通過“繪制”算法,以預測那些在數學上的***選擇。
決策樹通常是從單個節點開始的。該節點可以分支出各種可能性的結果。同時,這些結果都會導致新的節點產生,而這些節點則會繼續分枝出另一些其他類型的可能性。因此,這些最終形成一個樹狀的結構。
在決策樹中一般有三種不同類型的節點:機會節點、決策節點和末端節點(end node)。我們用圓形來表示的機會節點,代表某些結果的概率;用正方形來表示的決策節點,代表要做出的各種決策;結束節點表示某個決策路徑的最終結果。
決策樹的優缺點
優勢
- 決策樹能夠生成各種可理解的規則。
- 無需大量計算,決策樹即可執行分類。
- 決策樹能夠處理連續變量和分類變量。
- 決策樹能夠清楚地表明哪些字段對于預測或分類是最為重要的。
缺點
- 決策樹不太適合于那些目標為預測連續屬性值的估算類任務。
- 在面對有著多個類、和相對較少的訓練樣本的分類問題時,決策樹容易出現錯誤。
- 在訓練的過程中,決策樹在計算成本上的開銷比較高。在每個節點上,我們必須先對每個候選字段進行排序,然后才能找到其***的拆分方式。某些算法會使用字段的組合,以對***組合的權重進行搜索。另外,由于必須形成和比較各種候選子樹,因此修剪算法(Pruning algorithms,https://www.edureka.co/blog/implementation-of-decision-tree/)的開銷會更大。
創建決策樹
讓我們考慮一個場景,有一組天文學家發現了一顆新的行星,他們感興趣的問題是:它是否可能是下一個地球呢?
顯然,在做出明智的判斷之前,我們值得深入研究的決定性因素有許多,包括:該星球上是否存在著水、溫度是多少、地表是否容易持續遭受暴風雨的影響、動植物是否在此類特定的氣候中能生存活下來等方面。
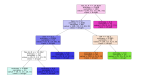
下面,讓我們通過創建一個決策樹,來判定它是否人類下一個“棲息地”。
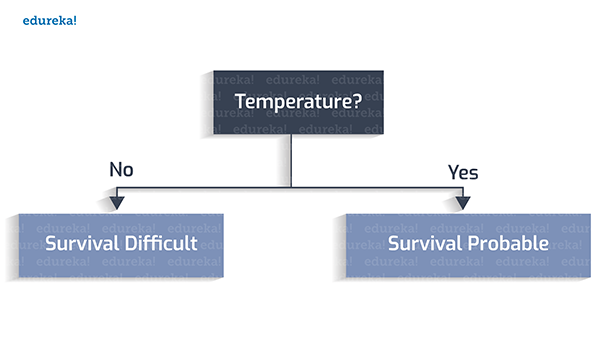
首先,我們設定宜居的溫度在0到100攝氏度之間。
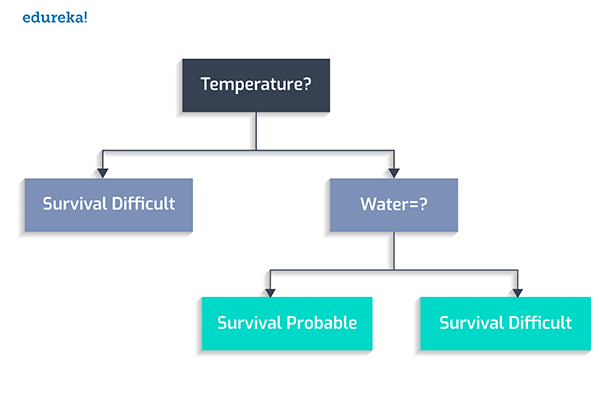
其次,是否存在著水?
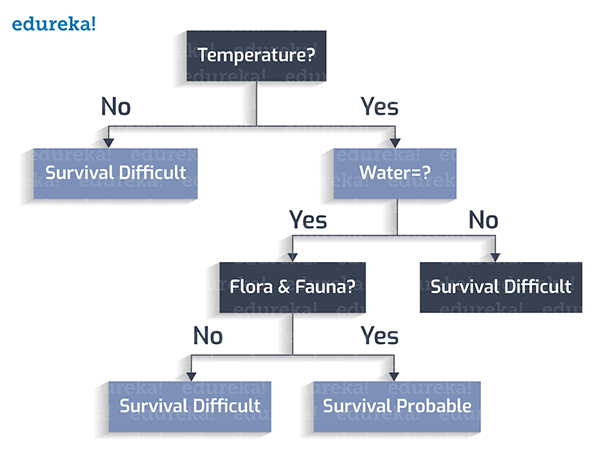
然后,動植物是否繁茂?
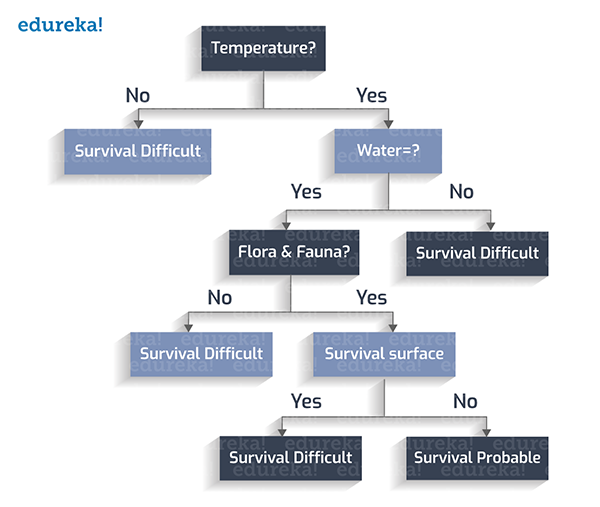
組后,該星球的表面是否有風暴?
至此,我們就得到了一個完整的決策樹。
分類規則
分類規則是:在考慮了所有的可能性之后,為每種方案分配一個類變量(class variable)的狀況。
類變量
我們為每一個葉節點都分配一個類變量。類變量將直接影響我們判斷的最終輸出。
下面讓我們從上面創建的決策樹中,推導出如下的分類規則:
1. 如果溫度不在273至373K(開爾文,熱力學單位)之間,則視為:生存困難。
2. 如果溫度在273至373K之間,且不存在水,則視為:生存困難。
3. 如果溫度在273至373K之間,存在水,但沒有動植物,則視為:生存困難。
4. 如果溫度在273至373K之間,存在水,存在動植物,且無地表暴風雨,則視為:生存可能。
5. 如果溫度在273至373K之間,存在水,存在動植物,但存在地表暴風雨,則視為:生存困難。
決策樹
本例的決策樹由如下部分組成:
- 根節點:在上例中,“溫度”因素被視為根。
- 內部節點:具有一個傳入邊(incoming edge)和兩到多個傳出邊(outgoing edge)的節點。
- 葉子節點:不再具有傳出邊的末端節點。
根據上述三個部分,我們從根節點開始,逐個檢查測試條件(test condition),并將判斷結果(或稱控制)分配給其中一個傳出邊,以便將其作為另一個節點的傳入邊,進行下一輪條件測試。當所有測試條件都遍歷完畢并到達葉子節點時,該決策樹完畢。而葉子節點則包含了是否認可該決策(判斷)的各種類標簽(class labels)。
您一定有些疑惑:為什么我們會將“溫度”屬性作為根,來構造決策樹呢?如果選擇其他屬性,將有什么不同呢?的確,不同的屬性特征會創建出許多不同的樹。我們需要通過遵循某種算法來選擇***的決策樹。下面我們來討論一種被稱為“貪婪法則(Greedy Approach)”的決策樹創建算法。
貪婪法則
根據維基百科,貪婪法則是基于啟發式問題解決(Heuristic Problem Solving)的概念,在每個節點上做出***的局部選擇。然后通過這些局部的***選擇,在全局范圍內找到了近似的***解。
該算法包括:
1. 在每個階段(節點),選擇出***特征作為測試條件。
2. 接著將節點拆分為各種可能性的輸出(內部節點)。
3. 重復上述步驟,直到所有測試條件都在葉子節點中被遍歷到。
我們回到剛才的問題:如何選擇初始的測試條件呢?這里會涉及到兩個概念:熵(Entropy)和信息增益(Information Gain)。
熵:在決策樹中,熵表示同質性。如果數據是完全均勻的,則熵為0;否則,如果數據被分割了(如50比50%),那么熵為1。
信息增益:信息增益表示節點被拆分時,其熵值的增與減。
我們的目的是,讓被選取進行拆分的屬性特征具有***的信息增益。因此,根據熵和信息增益的計算值,我們需要在任何特定步驟中,選取***的屬性。
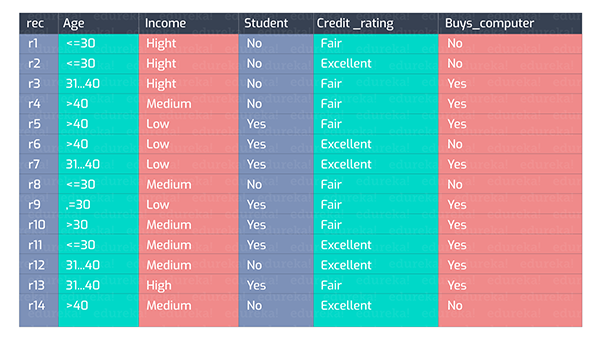
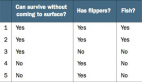
我們來看下圖的一組數據:
我們可以根據上圖中各種維度的屬性特征集合,得出一系列不同種類的決策樹。下面 是兩種創建試驗:
樹的創建試驗 1:
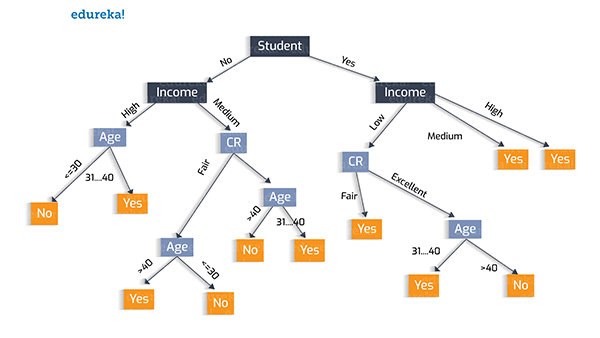
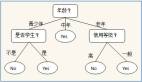
在此,我們使用“學生”,這一屬性特征作為初始化的測試條件,其決策樹如下圖所示。
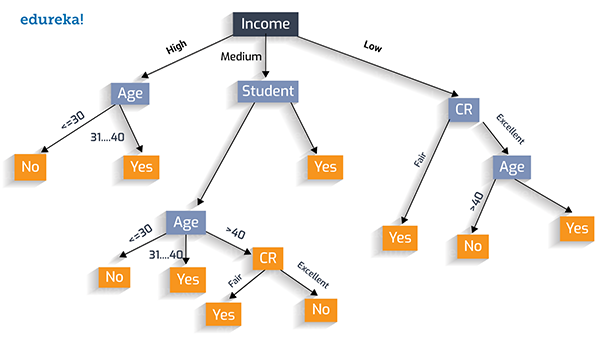
樹的創建試驗 2:
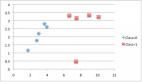
同樣,我們可以選擇“收入”作為測試條件,如下圖所示:
用貪婪法則創建***的決策樹
在此,我們涉及到兩個類:“Yes”表示此人會購買電腦;“No”表示不購買。為了計算熵和信息增益,我們來看看這兩個類分別的概率值。
»Positive:“buys_computer=yes”的概率為:
»Negative:“buys_computer=no”的概率為:
D的熵:我們將概率值放入上面的公式,以求出熵。
在準備階段,我們預先對熵的值進行了分類,它們分別為:
熵 = 0:數據完全是同質的 (純)
熵 = 1:數據被分為50%比50% (不純)
由于我們算出的熵值是0.940,可見是不純的。
下面讓我們通過深入研究,來找出合適的屬性特征,以計算信息增益。
如果我們在“年齡”上進行拆分,那么就能夠按照年齡的不同階段,來區分是否購買電腦產品。
例如,對于年齡在30歲及以下的人來說,有2人購買(Yes),3人不購買(No)電腦。那么我們針對三個年齡階段(將年齡屬性特征值進行拆分)的人,計算出針對***一列(是否購買電腦)的Info(D)。
可見,信息增益便是總的Info(0.940)與以年齡為屬性計算的Info(0.694)的差。
因此,這就是我們如果使用“年齡”為屬性進行拆分的因子。同理,我們也可以計算出其余屬性特征維度的“信息增益”,如:
信息增益 (年齡) = 0.246
信息增益 (收入) = 0.029
信息增益 (學生) = 0.151
信息增益 (信用評級) = 0.048
通過對上述值的綜合比較,我們不難發現:“年齡”的“信息增益”***,因此,拆分“年齡”是一個比較好的決策。
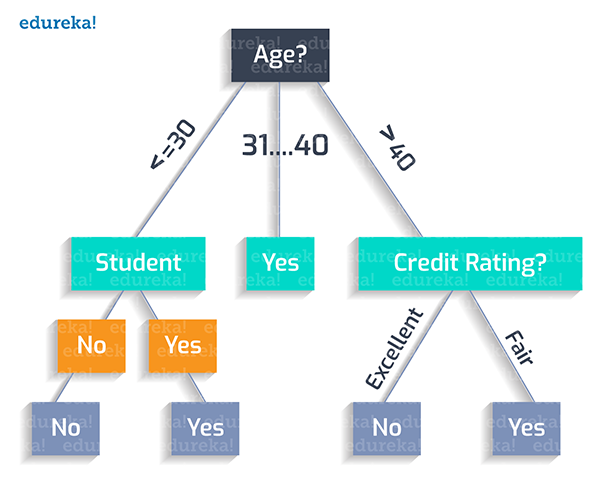
可見,我們應該創建的***決策樹應該如下圖所示:
由上圖可見,我們應該按照如下邏輯“繪制”出該決策樹的分類規則:
如果某人的年齡小于30歲,而且他不是學生,那么他就不會買產品。
Age (<30) ^ student(no) = NO
如果某人的年齡小于30歲,并且他是學生,那么他就會購買該產品。
Age (<30) ^ student(yes) = YES
如果某人的年齡在31歲至40歲之間,那么他最有可能購買產品。
Age (31…40) = YES
如果某人的年齡超過了40歲,且信用評級非常好,那么他就不會買產品。
Age (>40) ^ credit_rating(excellent) = NO
如果某人的年齡超過了40歲,且信用評級尚可,那么他很可能會購買產品。
Age (>40) ^ credit_rating(fair) = Yes
這便是我們根據上例所實現的***決策樹。
原文標題:How to Create a Perfect Decision Tree,作者:Upasana Priyadarshiny
【51CTO譯稿,合作站點轉載請注明原文譯者和出處為51CTO.com】