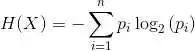本文轉(zhuǎn)載自公眾號“讀芯術(shù)”(ID：AI_Discovery)。

決策樹是機器學習中使用的最流行和功能最強大的分類算法之一。顧名思義，決策樹用于根據(jù)給定的數(shù)據(jù)集做出決策。也就是說，它有助于選擇適當?shù)奶卣饕詫浞殖深愃朴谌祟愃季S脈絡的子部分。

為了有效地構(gòu)建決策樹，我們使用了熵/信息增益和基尼不純度的概念。讓我們看看什么是基尼不純度，以及如何將其用于構(gòu)建決策樹吧。

[[375443]]

什么是基尼不純度?

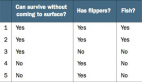
基尼不純度是決策樹算法中用于確定根節(jié)點的最佳分割以及后續(xù)分割的方法。這是拆分決策樹的最流行、最簡單的方法。它僅適用于分類目標，因為它只執(zhí)行二進制拆分。

基尼不純度的公式如下：

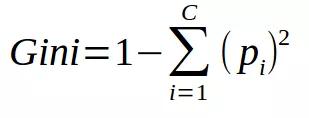
基尼不純度越低，節(jié)點的同質(zhì)性越高。純節(jié)點(相同類)的基尼不純度為零。以一個數(shù)據(jù)集為例，計算基尼不純度。

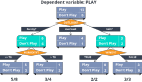
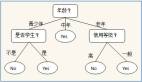
該數(shù)據(jù)集包含18個學生，8個男孩和10個女孩。根據(jù)表現(xiàn)將他們分類如下：

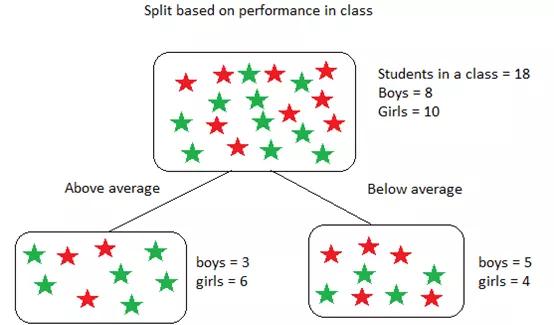
上述基尼不純度的計算如下：

上述計算中，為了找到拆分(根節(jié)點)的加權(quán)基尼不純度，我們使用了子節(jié)點中學生的概率。對于“高于平均值”和“低于平均值”節(jié)點，該概率僅為9/18，這是因為兩個子節(jié)點的學生人數(shù)相等，即使每個節(jié)點中的男孩和女孩的數(shù)量根據(jù)其在課堂上的表現(xiàn)有所不同，結(jié)果亦是如此。

如下是使用基尼不純度拆分決策樹的步驟：

• 類似于在熵/信息增益的做法。對于每個拆分，分別計算每個子節(jié)點的基尼不純度。
• 計算每個拆分的基尼不純度作為子節(jié)點的加權(quán)平均基尼不純度。
• 選擇基尼不純度值最低的分割。
• 重復步驟1-3，直到獲得同類節(jié)點。

基尼不純度小總結(jié)：

• 有助于找出根節(jié)點、中間節(jié)點和葉節(jié)點以開發(fā)決策樹。
• 被CART(分類和回歸樹)算法用于分類樹。
• 當節(jié)點中的所有情況都屬于一個目標時，達到最小值(零)。

總而言之，基尼不純度比熵/信息增益更受青睞，因為它公式簡單且不使用計算量大而困難的對數(shù)。