Python高級算法與數據結構:使用treap實現雙索引之一
前面介紹的堆結構只能對數據進行部分排序,也就是它只能知道部分元素的排序,例如從根節點出發,沿著左孩子或右孩子前行,我們能得知所遍歷的元素一定是遞增(小堆)或是遞減(大堆)關系,但是我們無法得知左子樹與右子樹兩部分節點的排序關系。
在很多應用場景下,我們不但需要堆的特性,例如快速知道數據最大值或最小值,同時還需要知道元素的排序信息,因此本節我們看看如何實現魚和熊掌如何兼得。假設我們有一系列數據,它的元素由兩部分組成,一部分對應商品的名稱,其類型為字符串,一部分對應商品的貨存數量,類型為整形,我們既需要將商品根據其名稱排序,同時我們又需要快速查詢當前貨存最小的商品,我們如何設計相應的算法和數據結構來滿足這樣特性呢。
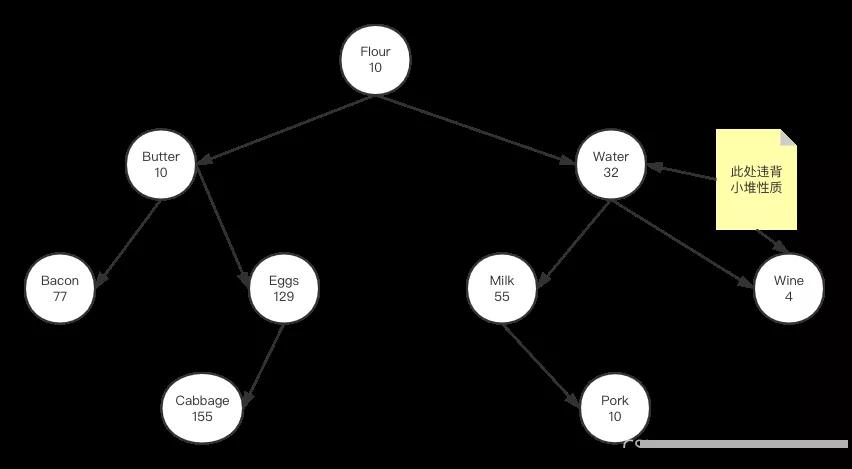
舉個例子,如下圖:
從上圖看,它對應元素字符串是排序二叉樹,因此根節點左子樹對應元素的字符串都小于根字符串,同時右子樹對應的字符串都大于根節點字符串,同時每個元素還對應著相應商品的貨存數量,我們需要及時掌握當前貨存最少的商品,這樣才能在其耗盡之前迅速補貨。但是從上圖可以看到,要保證字符串的排序性就得犧牲對于商品數量的小堆性質,例如上圖中water對應的貨存與wine對應的貨存違背了小堆的性質,現在問題是如何在保證字符串排序的情況下,確保數量同時能滿足小堆性質。
首先我們先定義一下數據結構:
- class Node:
- def __init__(self, key: str, priority: float):
- self._key = key
- self._priority = priority
- self._left: Node = None
- self._right: Node = None
- self._parent: Node = None
- @property
- def left(self):
- return self._left
- @property
- def right(self):
- return self._right
- @property
- def parent(self):
- return self._parent
- @left.setter
- def left(self, node):
- self._left = node
- if node is not None:
- node.parent = self
- @right.setter
- def right(self, node):
- self._right = node
- if node is not None:
- node.parent = self
- @parent.setter
- def parent(self, node):
- self._parent = node
- def is_root(self) -> bool:
- if self.parent is None:
- return True
- return False
- def __repr__(self):
- return "({}, {})".format(self._key, self._priority)
- def __str__(self):
- repr_str: str = ""
- repr_str += repr(self)
- if self.parent is not None:
- repr_str += " parent: " + repr(self.parent)
- else:
- repr_str += " parent: None"
- if self.left is not None:
- repr_str += " left: " + repr(self.left)
- else:
- repr_str += " left: None"
- if self.right is not None:
- repr_str += " right: " + repr(self.right)
- else:
- repr_str += " right: None"
- return repr_str
- class Treap:
- def __init__(self):
- self.root : Node = None
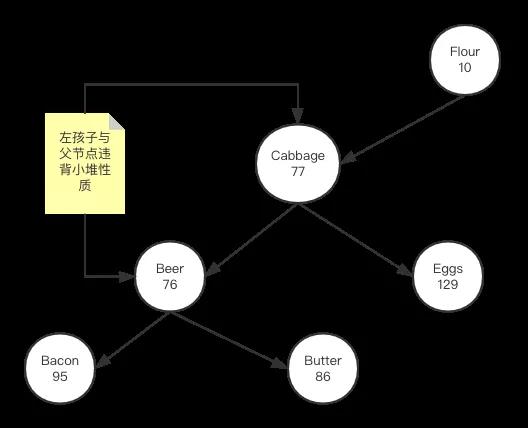
當前問題是,當上圖所示的矛盾出現時,我們如何調整,使得字符串依然保持排序性質,同時貨存數值能滿足小堆性質。我們需要根據幾種情況采取不同操作,首先看第一種,如下圖:
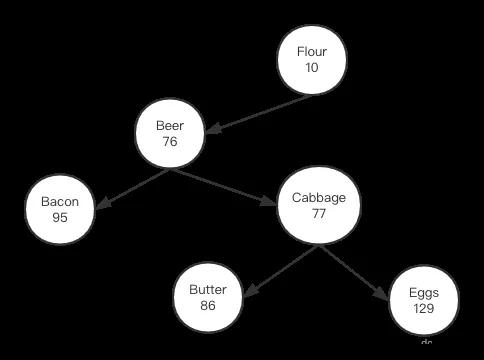
從上圖看到,一種情況是父節點與左孩子在數值上違背了堆的性質,此時我們執行一種叫右旋轉操作,其步驟是,1,Beer節點逆時針旋轉,替換其父節點;2,父節點Cabbage順時針旋轉,成為Beer的右孩子節點;3,原來Beer的右孩子節點轉變為Cabbage的左孩子節點;完成后結果如下圖所示:
可以看到,此時字符串依然保持排序二叉樹性質,同時數值對應的小堆性質也得到了滿足。我們看看代碼實現:
- class Treap:
- def __init__(self):
- self._root: Node = None
- def right_rotate(self, x: Node):
- if x is None or x.is_root() is True:
- return
- y = x.parent
- if y.left != x: # 必須是左孩子才能右旋轉
- return
- p = y.parent
- if p is not None: # 執行右旋轉
- if p.left == y:
- p.left = x
- else:
- p.right = x
- else:
- self._root = x
- y.left = x.right
- x.right = y
接下來我們構造一些數據測試一下上面的實現是否正確:
- def setup_right_rotate():
- flour: Node = Node("Flour", 10)
- cabbage: Node = Node("Cabbage", 77)
- beer: Node = Node("Beer", 76)
- bacon: Node = Node("Bacon", 95)
- butter: Node = Node("Butter", 86)
- flour.parent = None
- flour.left = cabbage
- flour.right = None
- cabbage.left = beer
- beer.left = bacon
- beer.right = butter
- return flour, beer
- def print_treap(n: Node):
- if n is None:
- return
- print(n)
- print_treap(n.left)
- print_treap(n.right)
- treap = Treap()
- root, x , cabbage = setup_right_rotate()
- print("---------before right rotate---------:")
- print_treap(root)
- treap.right_rotate(x)
- print("-------after right rotate-------")
- print_treap(root)
上面代碼執行后輸出內容如下:
- ---------before right rotate---------:
- (Flour, 10) parent: None left: (Cabbage, 77) right: None
- (Cabbage, 77) parent: (Flour, 10) left: (Beer, 76) right: (Eggs, 129)
- (Beer, 76) parent: (Cabbage, 77) left: (Bacon, 95) right: (Butter, 86)
- (Bacon, 95) parent: (Beer, 76) left: None right: None
- (Butter, 86) parent: (Beer, 76) left: None right: None
- (Eggs, 129) parent: (Cabbage, 77) left: None right: None
- -------after right rotate-------
- (Flour, 10) parent: None left: (Beer, 76) right: None
- (Beer, 76) parent: (Flour, 10) left: (Bacon, 95) right: (Cabbage, 77)
- (Bacon, 95) parent: (Beer, 76) left: None right: None
- (Cabbage, 77) parent: (Beer, 76) left: (Butter, 86) right: (Eggs, 129)
- (Butter, 86) parent: (Cabbage, 77) left: None right: None
- (Eggs, 129) parent: (Cabbage, 77) left: None right: None
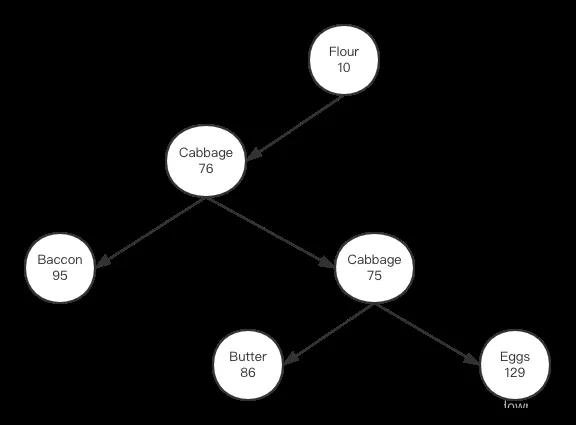
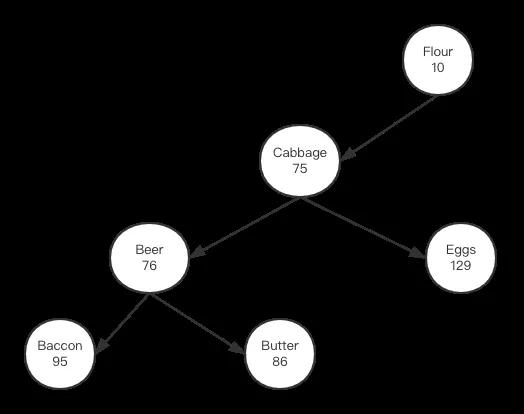
對比右旋轉前后輸出的二叉樹看,旋轉后的二叉樹打印信息的確跟上面我們旋轉后對應的圖像是一致的。接下來我們實現左旋轉,先把上圖中cabbage節點對應的值改成75,這樣它與父節點就違背了小堆性質:
我們要做的是:1,把cabbage節點向“左”旋轉到beer的位置;2,beer的父節點設置為cabbage;3:beer的右孩子設置為cabbage的左孩子;4,cabbage的左孩子變成beer;左旋轉后二叉樹應該成形如下:
從上圖看,左旋轉后,字符串依然保持二叉樹排序性,同時數值的排放也遵守小堆原則,我們看相應的代碼實現:
- class Treap:
- ...
- def left_rotate(self, x : Node):
- if x is None or x.is_root() is True:
- return
- y = x.parent
- if y.right is not x: # 只有右孩子才能左旋轉
- return
- p = y.parent
- if p is not None:
- if p.left is y:
- p.left = x
- else:
- p.right = x
- else:
- self._root = x
- y.right = x.left
- x.left = y
為了測試上面代碼實現,我們首先把cabbage的值修改,然后調用上面代碼:
- cabbage._priority = 75
- print("-------before left rotate--------")
- print_treap(root)
- treap.left_rotate(cabbage)
- print("-------after left rotate---------")
- print_treap(root)
代碼運行后輸出結果為:
- -------before left rotate--------
- (Flour, 10) parent: None left: (Beer, 76) right: None
- (Beer, 76) parent: (Flour, 10) left: (Bacon, 95) right: (Cabbage, 75)
- (Bacon, 95) parent: (Beer, 76) left: None right: None
- (Cabbage, 75) parent: (Beer, 76) left: (Butter, 86) right: (Eggs, 129)
- (Butter, 86) parent: (Cabbage, 75) left: None right: None
- (Eggs, 129) parent: (Cabbage, 75) left: None right: None
- -------after left rotate---------
- (Flour, 10) parent: None left: (Cabbage, 75) right: None
- (Cabbage, 75) parent: (Flour, 10) left: (Beer, 76) right: (Eggs, 129)
- (Beer, 76) parent: (Cabbage, 75) left: (Bacon, 95) right: (Butter, 86)
- (Bacon, 95) parent: (Beer, 76) left: None right: None
- (Butter, 86) parent: (Beer, 76) left: None right: None
- (Eggs, 129) parent: (Cabbage, 75) left: None right: None
輸出結果的描述與上圖左旋轉后的結果是一致的。由于Treap相對于元素的key是排序二叉樹,因此在給定一個字符串后,我們很容易查詢字符串是否在Treap中,其本質就是排序二叉樹的搜索,其實現我們暫時忽略。
雖然查詢很簡單,但是插入節點則稍微麻煩,因為插入后,新節點與其父節點可能會違背小堆性質,因此在完成插入后,我們還需使用上面實現的左旋轉或右旋轉來進行調整。