神經網絡中常見的激活函數
深度學習中已經成為了人工智能領域的必備工具,源于人工神經網絡的研究,含多個隱藏層的多層感知器就是一種深度學習結構。尋找隱藏層的權重參數和偏置的過程,就是常說的“學習”過程,其遵循的基本原則就是使得網絡最終的輸出誤差最小化。在神經?絡中,激活函數是必須選擇的眾多參數之?,從而使神經?絡獲得最優的結果和性能。
經常用到的激活函數有哪些呢?如何進行選擇呢?
關于激活函數
激活函數(Activation Function),就是在人工神經網絡的神經元上運行的函數,負責將神經元的輸入映射到輸出端,激活函數將神經網絡中將輸入信號的總和轉換為輸出信號。激活函數大多是非線性函數,才能將多層感知機的輸出轉換為非線性,使得神經網絡可以任意逼近任何非線性函數,進而可以應用到眾多的非線性模型中。
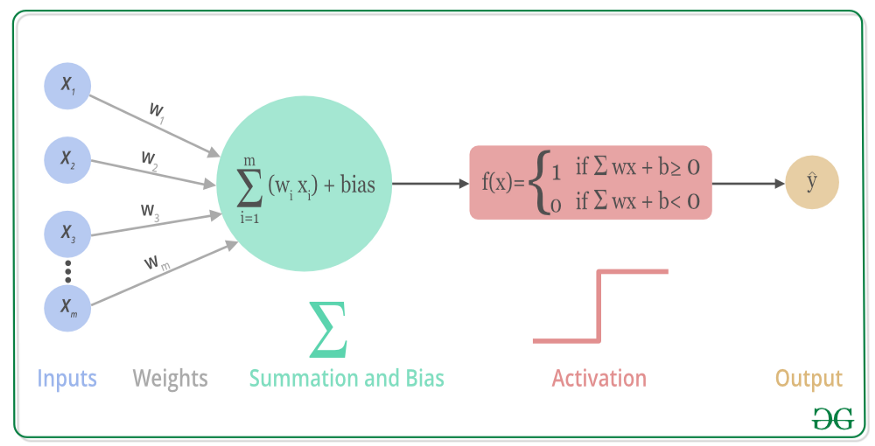
也就是說,非線性激活函數可以創建輸入與輸出鍵的復雜映射關系,神經網絡也能通過“學習”來更新參數。并且,因為非線性函數的導數與輸入有關,從而可以通過向后傳播算法計算梯度,也可以構建多層神經網絡,以處理復雜問題。
常見的激活函數有用于淺層網絡的sigmoid 系列,用于深層網絡的ReLU系列,用于遞歸網絡的tanh系列以及Softmax 系列等等。
sigmoid 系列
sigmoid函數也叫Logistic函數,用于隱層神經元輸出,能將( ? ∞ , + ∞ )的數值映射到(0,1)的區間,當以概率形式表示預測值時,一般使用這個函數。sigmod激活函數的Python 代碼如下:
import numpy as np
def sigmoid(x):
s = 1 / (1 + np.exp(-x))
return s
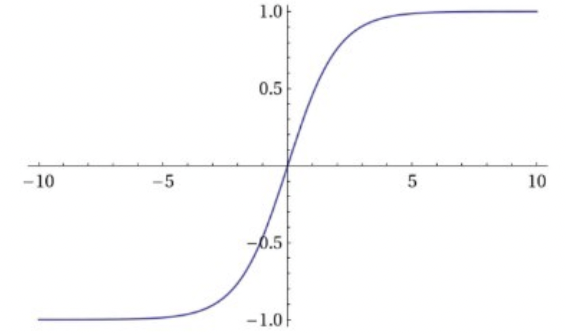
函數的圖像如下所示:
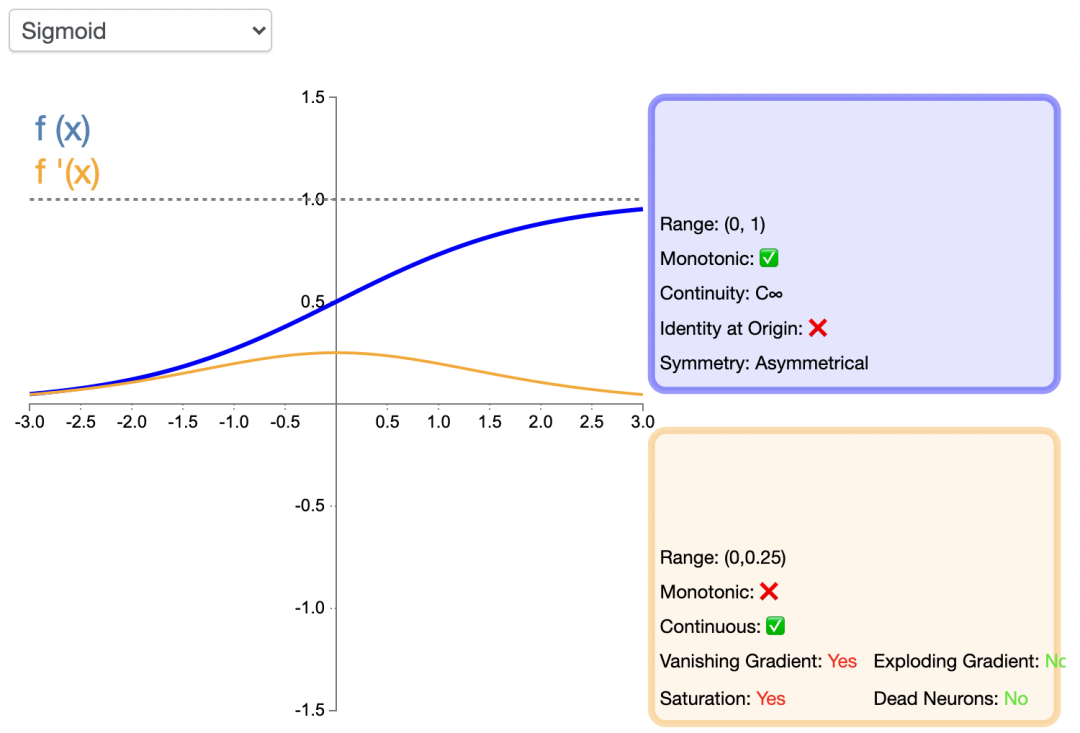
Sigmoid函數的優點在于它可導,并且值域在0到1之間,使得神經元的輸出標準化,是神經網絡最早采用的激活函數。它的不足也很明顯,在增加或減少到一定程度時,函數值變化很小,這就是所謂的“梯度消失”,致使網絡的收斂速度變慢,進而耗費計算資源。另外,輸出值不是以0為中心,而是0.5。
一般的Sigmoid 函數應用于淺層網絡。
HardSigmoid
在Sigmoid的基礎上,又有HardSigmoid,因為當輸入值趨向無窮大的時候,輸出值趨向于1;當輸入值趨向無窮小的時候,輸出值趨向于0。所以,顧名思義,HardSigmoid是在Sigmoid的基礎上,當輸入值超過某個范圍強行置1和0。HardSigmoid 的python 代碼如下:
def Hard_sigmoid(x):
y = []
for i in x:
if i < -2.5:
y_i = 0
elif i >= -2.5 and i <= 2.5:
y_i = 0.2 * i + 0.5
else:
y_i = 1
y.append(y_i)
return y
HardSigmoid 激活函數的函數圖像如下:
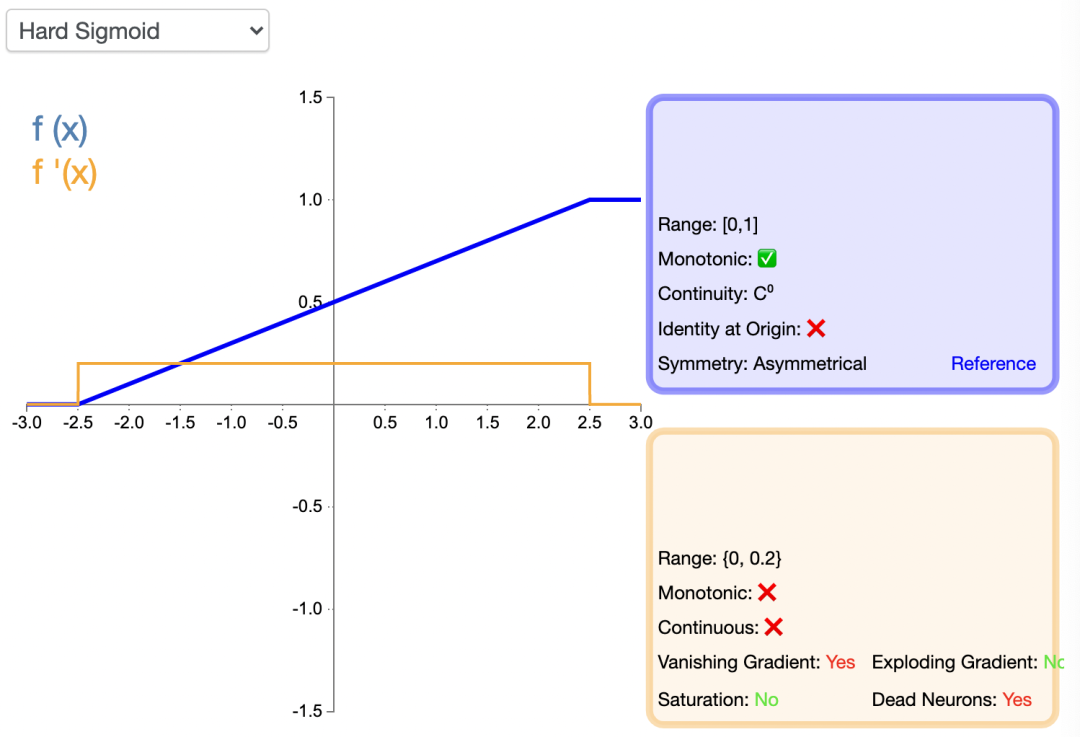
Swish
swish的表達式為:f ( x ) = x ? s i g m o i d ( b x ),python代碼如下:
def Swish(x):
return x / (1 + np.exp(-b*x))
其中b是可學參數, Swish 具備無上界有下界、平滑、非單調的特性。
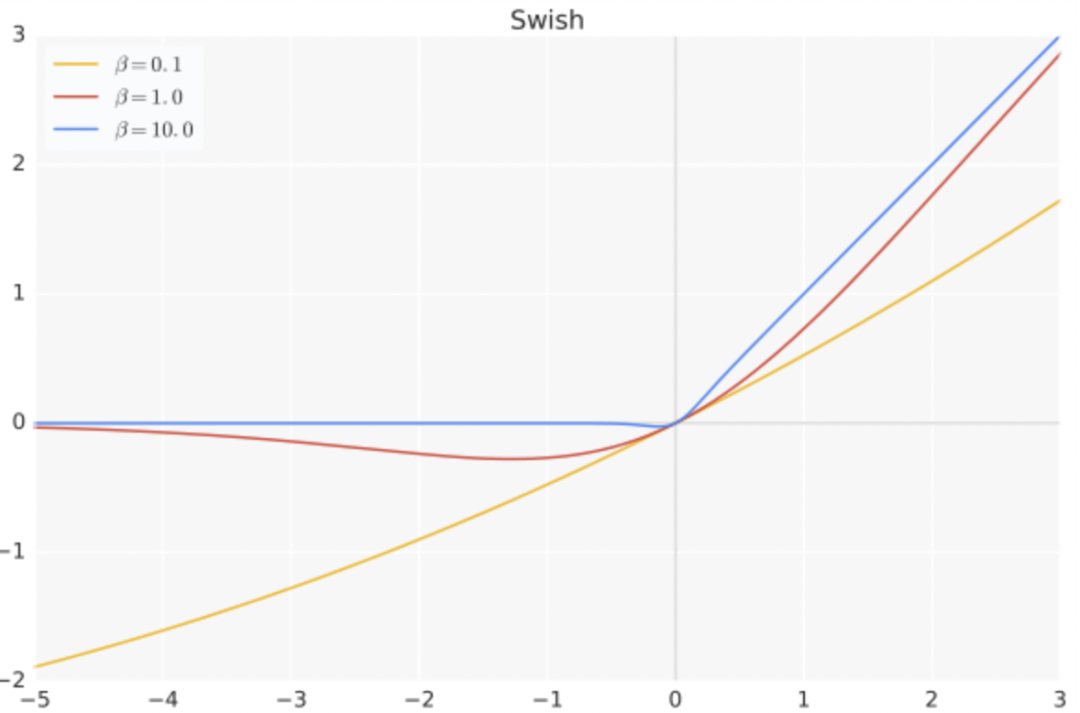
Swish 在深層模型上的效果優于 ReLU。例如,僅僅使用 Swish 單元替換 ReLU 就能把 Mobile NASNetA 在 ImageNet 上的分類準確率提高 0.9%。
maxout
Maxout可以看做是在深度學習網絡中加入一層激活函數層,包含一個參數k。這一層相比ReLU,sigmoid等,其特殊之處在于增加了k個神經元,然后輸出激活值最大的值。
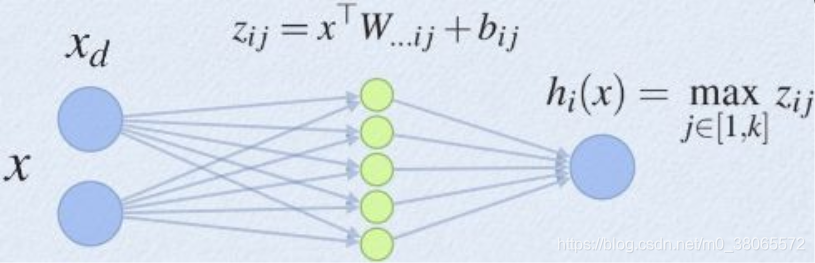
maxout是一個函數逼近器,對于一個標準的MLP網絡來說,如果隱藏層的神經元足夠多,那么理論上是可以逼近任意的函數的。Maxout的擬合能力非常強,可以擬合任意的凸函數,具有ReLU的所有優點,線性、不飽和性,同時沒有ReLU的一些缺點,如神經元的死亡。
Relu系列
Relu (Rectified Linear Unit)稱為“線性整流函數”或者“修正線性單元”,通常就直接稱為 ReLU 函數,是解決梯度消失問題的方法。將 ReLU 函數引入神經網絡時,也引入了很大的稀疏性。然而,由于稀疏性,時間和空間復雜度更低,不涉及成本更高的指數運算,允許網絡快速收斂。
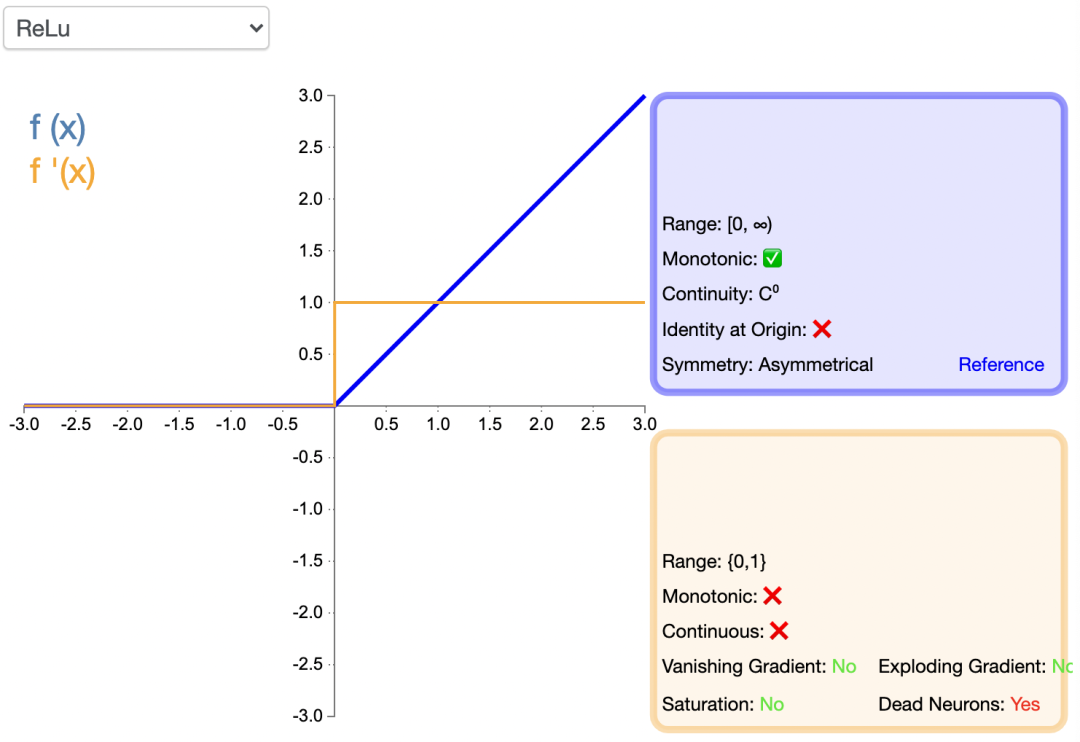
盡管Relu看起來像線性函數,但它具有導數函數并允許反向傳播,python 代碼如下:
import numpy as np
def relu(x):
s = np.where(x < 0, 0, x)
return s
ReLU引入了神經元死亡問題,當輸入接近零或為負時,函數的梯度變為零,網絡將無法執行反向傳播,也無法學習,也就是說,網絡的大部分分量都永遠不會更新,另外,它不能避免梯度爆炸問題。
ReLU是現在DNN模型中比較常用的激活函數。
ELU
指數線性單元激活函數ELU解決了 ReLU 的一些問題,同時也保留了一些好的方面。這種激活函數要選取一個 α 值;常見的取值是在 0.1 到 0.3 之間。但α =0.3時的函數圖像如下:
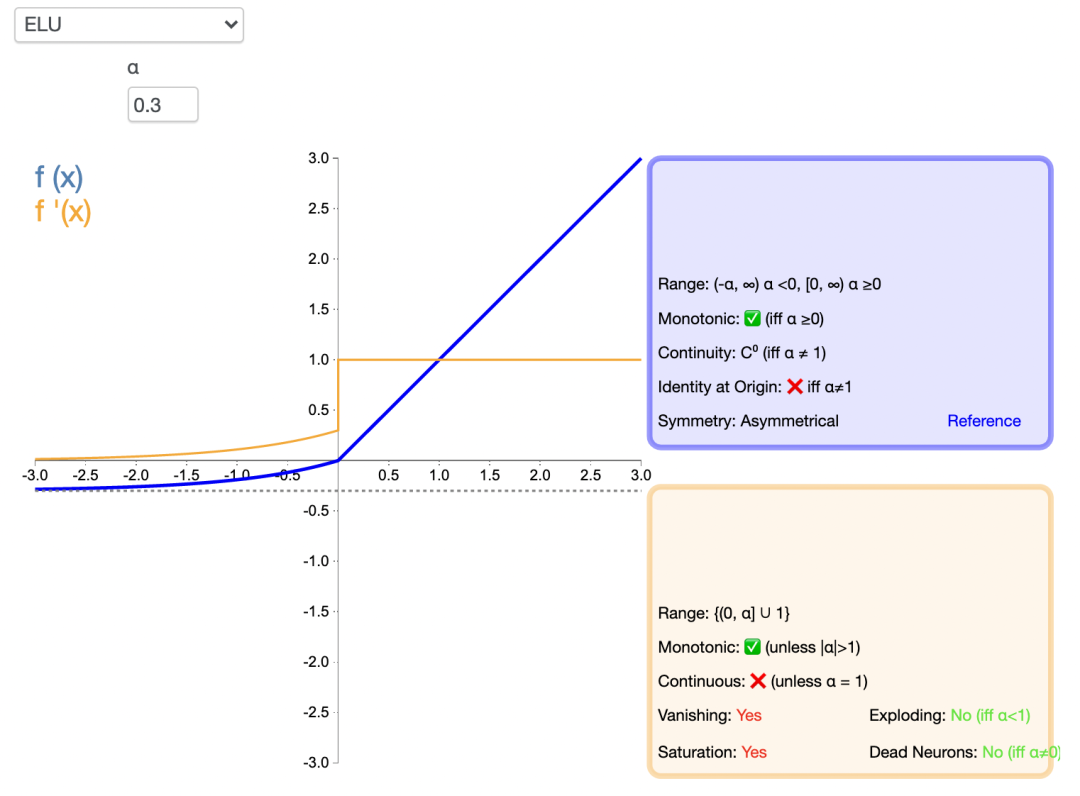
ELU能避免神經元死亡問題,能得到負值輸出,這能幫助網絡向正確的方向推動權重和偏置變化,在計算梯度時能得到激活,而不是讓它們等于 0。ELU 的python 代碼如下:
import numpy as np
def elu(x):
s = np.where(x >= 0, x, α(np.exp(x)-1)
return s
但是,由于包含了指數運算,計算時間更長,同樣無法避免梯度爆炸問題,另外,神經網絡不學習 α 值。
Leaky ReLU
滲漏型整流線性單元激活函數也有一個 α 值,通常取值在 0.1 到 0.3 之間。Leaky ReLU 激活函數很常用,相比于 ELU 也有一些缺陷,但比 ReLU 具有一些優勢。
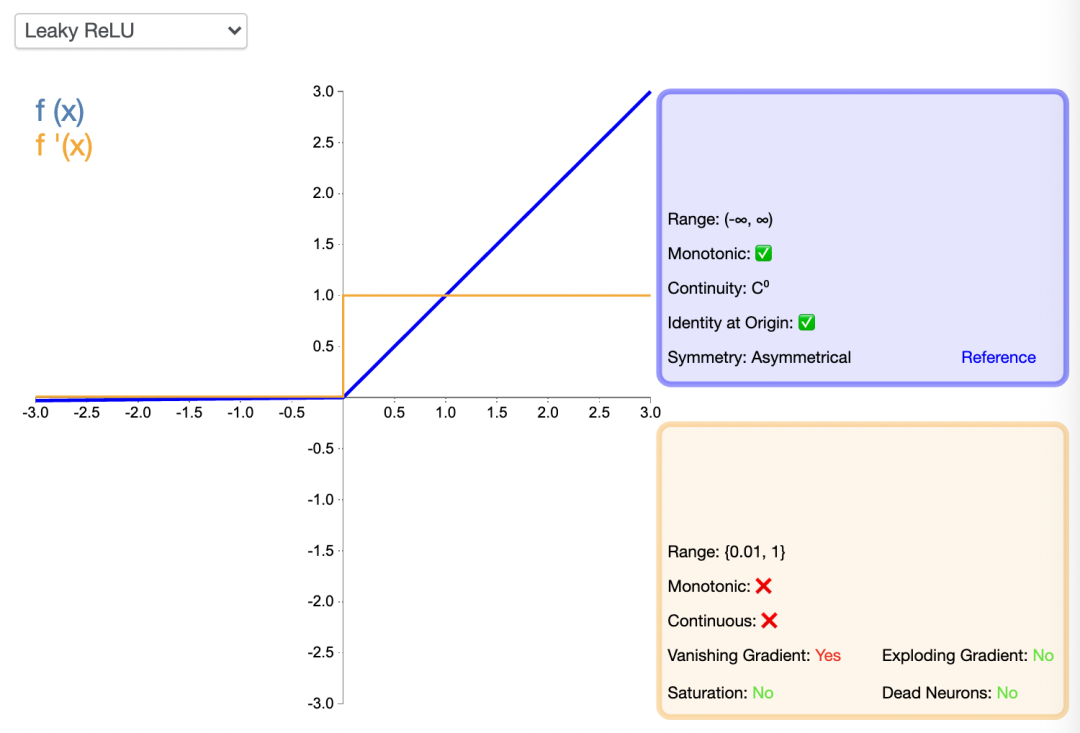
LeakyReLU的負值斜率很小,而不是平坦的斜率。斜率系數需要在訓練前確定,即在訓練過程中不學習。這種類型的激活函數在可能遇到稀疏梯度的任務中很流行,例如訓練生成式對抗網絡。
import numpy as np
def lrelu(x):
s = np.where(x >= 0, x, αx)
return s
類似 ELU,Leaky ReLU 也能避免死亡 ReLU 問題,因為其在計算導數時允許較小的梯度,由于不包含指數運算,所以計算速度比 ELU 快。
擴展型指數線性單元激活函數(SELU)
SELU 激活能夠對神經網絡進行自歸一化,歸一化就是首先減去均值,然后除以標準差。因此,經過歸一化之后,網絡的組件(權重、偏置和激活)的均值為 0,標準差為 1,而這正是 SELU 激活函數的輸出值。通過歸一化,網絡參數會被初始化一個正態分布。
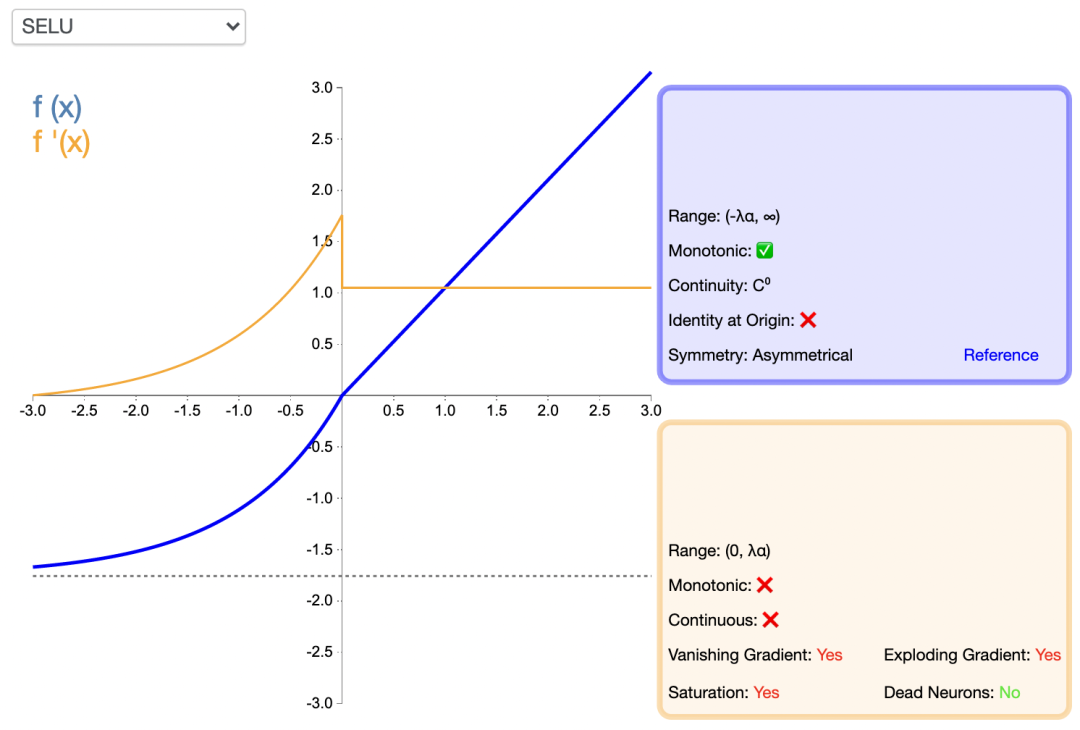
通過歸一化,網絡參數會被初始化一個正態分布。
def SeLU(x,alpha=1.6732632423543772848170429916717,scale=1.0507009873554804934193349852946):
y = []
for i in x:
if i >= 0:
y_i = scale * i
else:
y_i = scale * alpha * (np.exp(i) - 1)
y.append(y_i)
return y
SELU內部歸一化的速度比外部歸一化快,這意味著網絡能更快收斂,而且避免了出現梯度消失或爆炸問題,在CNN或RNN 網絡架構中有所應用。
高斯誤差線性單元激活函數GELU
GELU是某些函數(比如雙曲正切函數 tanh)與近似數值的組合,
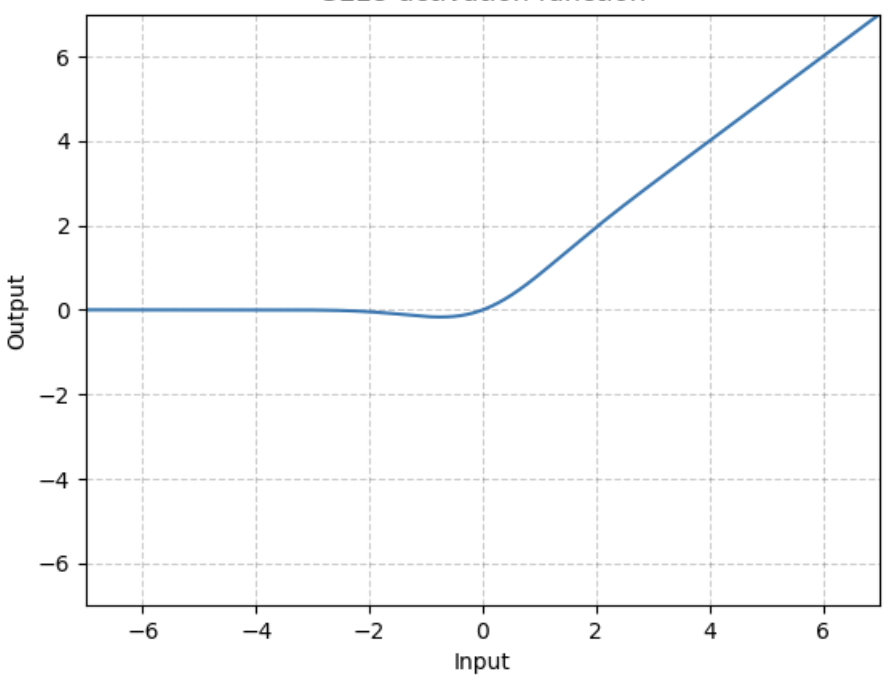
當 x 大于 0 時,輸出為 x;但 x=0 到 x=1 的區間除外,這時曲線更偏向于 y 軸。
import numpy as np
def tanh(x):
s1 = np.exp(x) - np.exp(-x)
s2 = np.exp(x) + np.exp(-x)
s = s1 / s2
return s
gelu = lambda x:0.5 * x * (1 + tanh(np.sqrt(2 / np.pi) * (x + 0.044715 * np.power(x, 3))))
GELU 在NLP 領域有較好表現,尤其在 Transformer 模型中表現最好,能避免梯度消失問題。
tanh系列
tanh
Tanh函數,即雙曲正切函數,比sigmoid函數更受歡迎,能為多層神經網絡提供更好的性能。
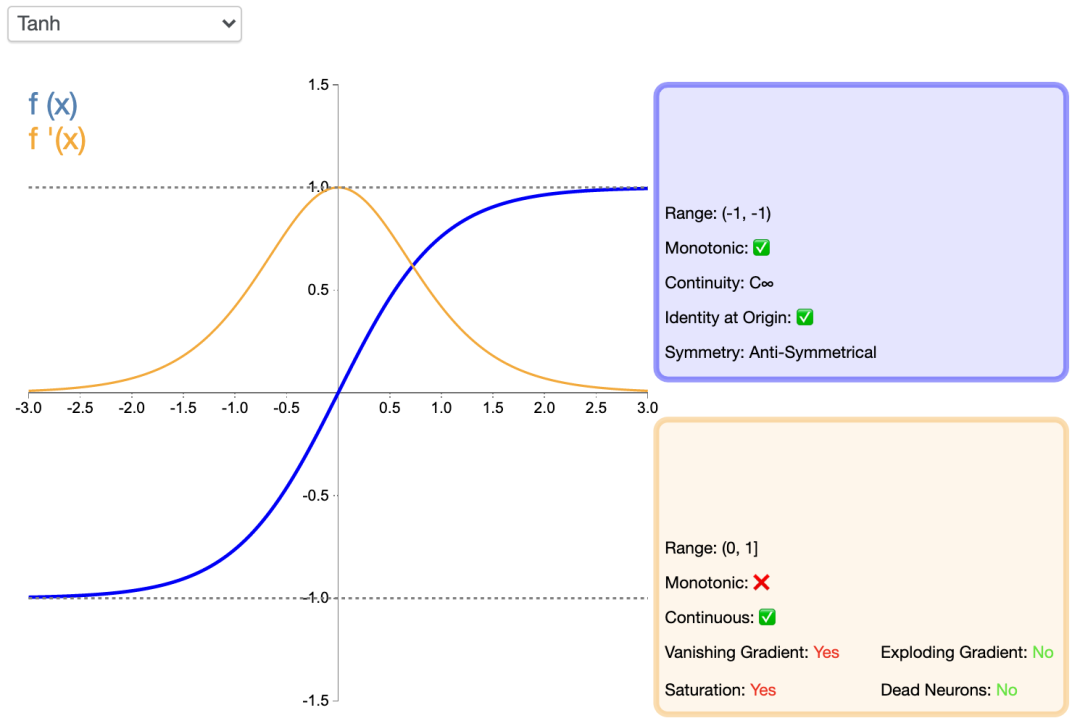
它的輸出更多地以零為中心,這有助于加速收斂,尤其是在訓練初期。雙曲線正切函數的python代碼如下:
import numpy as np
def tanh(x):
s1 = np.exp(x) - np.exp(-x)
s2 = np.exp(x) + np.exp(-x)
s = s1 / s2
return s
Tanh函數的最大優點是輸出值以 0為中心,即關于坐標原點對稱,分屬為正數和負數兩大類別,函數及其導數都是單調的,收斂速度比sigmoid快,從而可以減少迭代次數。這使得它具有了Sigmoid函數的優勢,又克服了某些不足。但是,“梯度消失”的問題都還存在,進而導致收斂速度變慢。
Tanh 一般用于遞歸神經網絡。
HardTanh
Hardtanh激活函數是Tanh的線性分段近似。相較而言,它更易計算,這使得學習計算的速度更快,盡管首次派生值為零可能導致靜默神經元/過慢的學習速率。
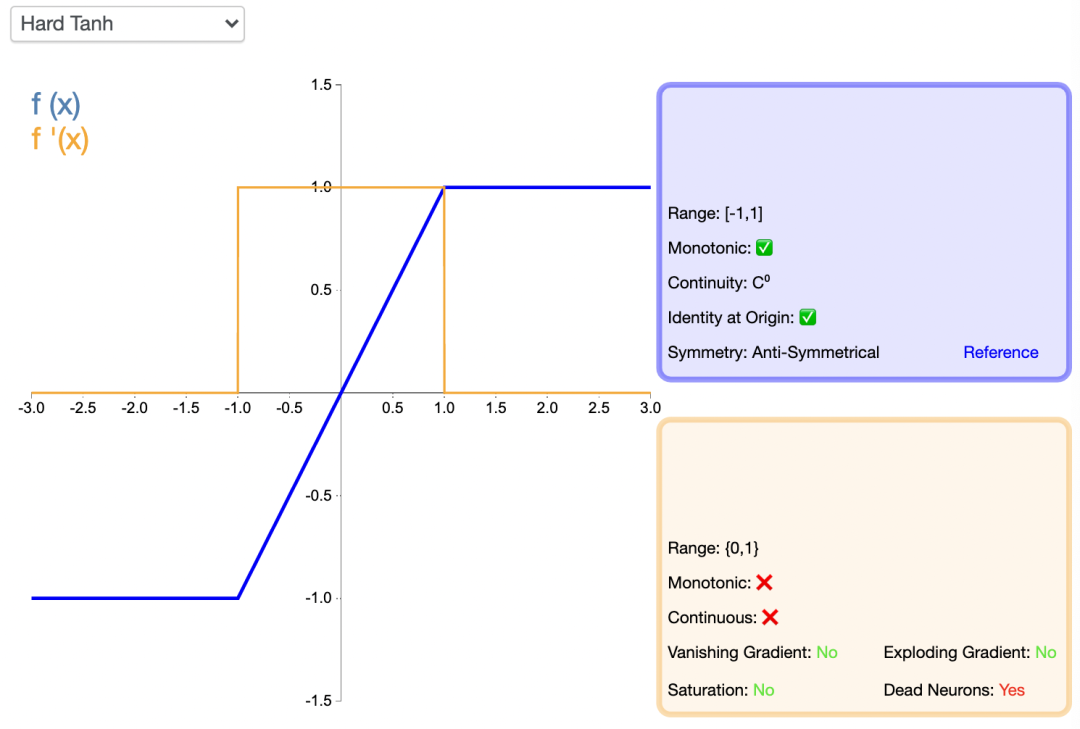
TanhShrink
基于Tanh之上,計算輸入輸出的差值,即為TanhShrink,函數圖像如下。
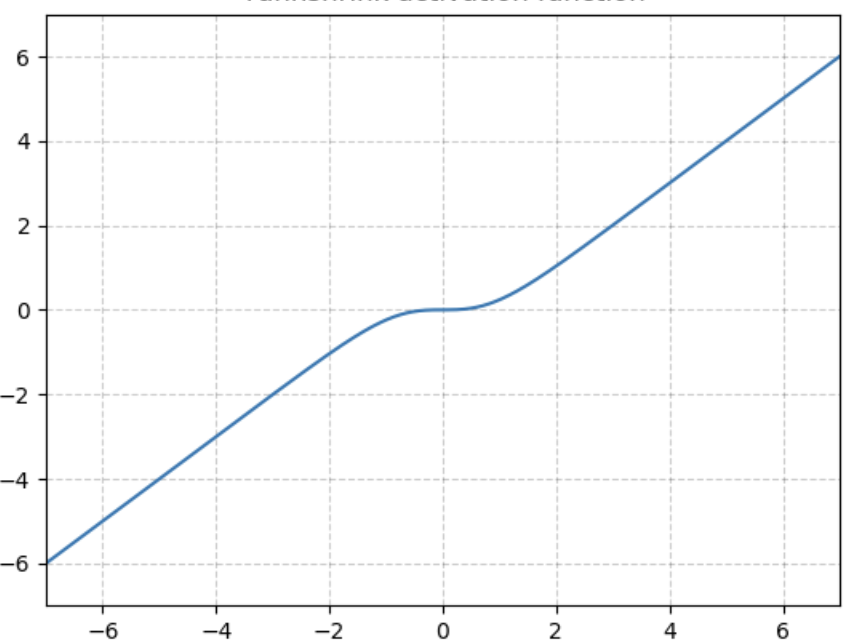
在當輸入在0附近時,梯度近乎為0,而在輸入極大或極小時,梯度反而為正常梯度。
softmax 系列
Softmax函數比較適合作為多分類模型的激活函數,一般會與交叉熵損失函數相配。
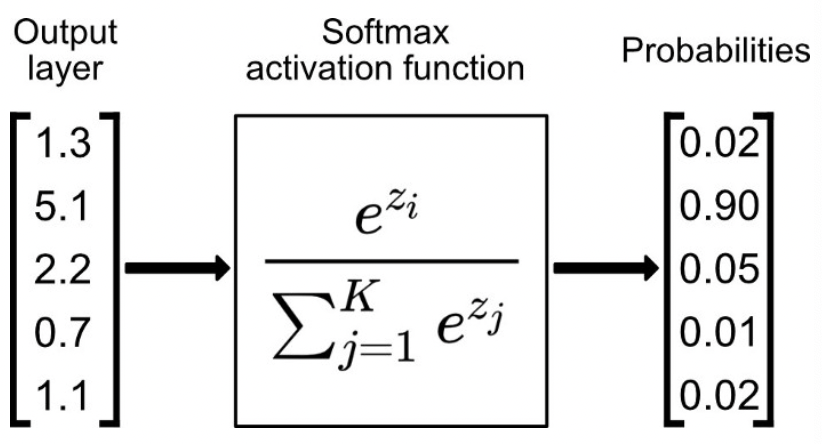
通常,Softmax函數只應用于輸出層,把一堆實數的值映射到0-1區間,并且使他們的和為1,可以理解為對應每個類別對應的預測概率。python代碼如下:
def softmax(x):
x_exp = np.exp(x)
x_sum = np.sum(x_exp, axis=1, keepdims=True)
s = x_exp / x_sum
return s
如果某一個zj大過其他z,那這個映射的分量就逼近于1,其他就逼近于0。
Softmax函數用于將輸入進行歸一化到(0,1),并且其和為1,普遍應用于分類模型(互斥)的預測概率值。事實上,但凡涉及到概率的地方基本都會用到softmax,典型的就比如attention layer當中,都會使用softmax來計算attention值。
LogSoftMax
LogSoftmax是基于Softmax函數之上,計算其對應的對數值,范圍在(-∞,0)用來計算交叉熵損失函數(根據groundtruth的標簽取出對應的值即可)。LogSoftMax 加快了運算速度,提高數據穩定性。
Softmin
Softmin是在Softmax的基礎上,做相反變換。Softmin是在Softmax的基礎上,做相反變換。 跟softmax類似,輸入n維t數據,對它們進行重新縮放使得n維輸出的每個元素都在[0, 1]區間內,且和為1。不同的是,softmax是單調遞增而softmin是單調遞減,意味著softmax操作會使得最大的值在激活操作后依然保持最大,而softmin會使得最小的數在經過了softmin后變成最大值。
激活函數的選擇
以終為始,激活函數的選擇也是為最終的任務目標服務的。不存在普遍適用各種神經網絡的萬能的激活函數,在選擇激活函數的時候,要考慮不同的條件限制,例如,如果函數可導,求導數的計算難度如何?函數光滑程度如何?輸出是否保持標準化?網絡的收斂速度如何?等等。
一般地,在用于分類器時,Sigmoid函數及其組合通常效果更好。為了避免梯度消失問題,又需要避免使用Sigmoid和TanH。如果是回歸模型,在輸出層上可以使用線性激活函數。如果是淺層神經網絡,如不超過4層的,可選擇使用多種激勵函數,沒有太大的影響。如果網絡中存在大量未激活神經元,可以考慮leaky ReLU函數。
ReLU函數是應用比較廣泛的激活函數,可以作為默認選項。深度學習往往需要大量時間來處理大量數據,模型的收斂速度是尤為重要的所以要盡量選擇輸出具有zero-centered特點的激活函數以加快模型的收斂速度。
一個經驗上的建議是:SELU > ELU > Leaky ReLU > ReLU> tanh > sigmoid,但是,如果網絡的體系結構阻止自歸一化,那么 ELU 可能是比 SELU 更好的選擇。如果速度很重要,Leaky ReLU 將是比慢很多的 ELU 更好的選擇。
更重要的是,激活函數仍在發展,需要跟蹤業界的最新進展,并勇于探索和創新。
一句話小結
激活函數是神經網絡中的重要參數,一般地,Sigmoid 系列用于二分類任務輸出層,softmax系列用于多分類任務輸出層,tanh系列用于模型隱藏層,Relu系列用于回歸任務以及卷積神經網絡隱藏層。但事無絕對,而且,新研究的激活函數仍在涌現。
附,reddit上有一張激活函數的圖,挺有意思的!