多智能體路徑規劃新突破:AA-CCBS算法詳解
多智能體路徑規劃(MAPF)是一個在機器人、交通控制和自動化倉庫等領域具有廣泛應用的重要問題。MAPF的核心目標是為一組智能體找到一組無沖突的路徑,使它們能夠從起點移動到目標位置。傳統的MAPF問題通常限制智能體只能在預定義的圖上移動,這種限制在實際應用中可能不夠靈活。
任意角度路徑規劃(Any-Angle Pathfinding)是一種更為靈活的方法,允許智能體在不碰撞障礙物的情況下在任意位置之間移動。這種方法在提高路徑規劃效率和適應復雜環境方面具有顯著優勢。然而任意角度路徑規劃也帶來了新的挑戰,特別是在多智能體環境中,如何確保路徑的無沖突性和最優性成為一個關鍵問題。
被IROS 2024會議接收論文《Optimal and Bounded Suboptimal Any-Angle Multi-agent Pathfinding》提出了第一個針對任意角度多智能體路徑規劃的最優算法,并介紹了其有界次優變體。這些算法在解決復雜路徑規劃問題時表現出色,具有重要的理論和實際意義。通過引入連續沖突搜索(CCBS)和安全區間路徑規劃(TO-AA-SIPP),以及多約束(MC)和分離拆分(DS)技術,論文的算法顯著提高了路徑規劃的效率和效果。
研究團隊由Konstantin Yakovlev、Anton Andreychuk和Roni Stern組成,他們分別隸屬于多個知名研究機構。Konstantin Yakovlev隸屬于FRC CSC RAS(俄羅斯科學院計算機科學與控制研究中心)、AIRI(人工智能研究所)、HSE University(高等經濟學院)和MIPT(莫斯科物理技術學院)。Anton Andreychuk隸屬于AIRI(人工智能研究所)。Roni Stern隸屬于Ben-Gurion University of the Negev(內蓋夫本-古里安大學)。他們在多智能體路徑規劃領域具有豐富的研究經驗和深厚的學術背景,為論文的研究提供了堅實的基礎。
研究背景
多智能體路徑規劃(MAPF)是一個在機器人、交通控制和自動化倉庫等領域具有廣泛應用的重要問題。MAPF的核心目標是為一組智能體找到一組無沖突的路徑,使它們能夠從起點移動到目標位置。傳統的MAPF問題通常限制智能體只能在預定義的圖上移動,這種限制在實際應用中可能不夠靈活。
近年來,研究人員開始探索放寬這些經典假設的方法。Yakovlev和Andreychuk提出了一種基于優先級規劃的任意角度MAPF算法,這種算法允許智能體在不碰撞障礙物的情況下在任意位置之間移動。這一方法在提高路徑規劃效率和適應復雜環境方面具有顯著優勢。然而任意角度路徑規劃也帶來了新的挑戰,特別是在多智能體環境中,如何確保路徑的無沖突性和最優性成為一個關鍵問題。
其他研究也提出了支持運動學約束的技術。例如,Yan和Li提出了一種基于優先級搜索的三階段求解器,能夠處理加速和減速動作。這些研究雖然在一定程度上解決了MAPF中的一些問題,但它們大多不是最優的。
在最優MAPF求解器方面,許多研究是對沖突基搜索(CBS)的改進。例如,Solis等人提出了為每個機器人構建路線圖并使用CBS進行規劃的方法,并結合軌跡優化方法為異構智能體團隊(如四旋翼機)構建無碰撞路徑。Kinodynamic變體的CBS也被提出,用于處理具有不同運動學特性的智能體。
盡管這些研究在一定程度上解決了MAPF中的一些問題,但它們大多集中在經典MAPF假設的基礎上。論文的研究旨在進一步放寬這些假設,提出一種新的任意角度多智能體路徑規劃算法(AA-CCBS),并通過引入多約束(MC)和分離拆分(DS)技術來提高算法的效率和效果。
問題陳述
在多智能體路徑規劃(MAPF)中,目標是為一組智能體找到一組無沖突的路徑,使它們能夠從起點移動到目標位置。傳統的MAPF問題通常限制智能體只能在預定義的圖上移動,這種限制在實際應用中可能不夠靈活。論文研究的任意角度多智能體路徑規劃問題(AA-MAPF)則放寬了這一限制,允許智能體在不碰撞障礙物的情況下在任意位置之間移動。
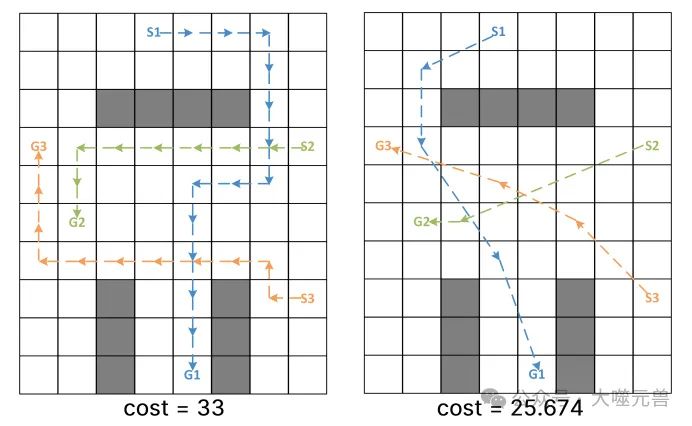
圖1:同一MAPF實例的兩個最優解:由基數組成的一個只移動(左),而具有任何角度的一個移動(右)。后者的成本降低了22%。
具體來說,AA-MAPF問題的目標是找到一組將智能體從起點傳送到目標位置的無沖突路徑,并且這些路徑的總成本最小。每個智能體可以在任意角度上移動,只要它們的路徑不與障礙物相交。這種任意角度的移動方式使得路徑規劃更加靈活和高效,但也帶來了新的挑戰,特別是在多智能體環境中,如何確保路徑的無沖突性和最優性成為一個關鍵問題。
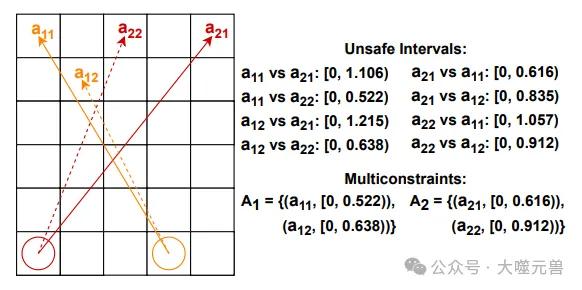
圖2:vanilla AA-CCBS多約束的示例。
論文提出的AA-CCBS算法結合了連續沖突搜索(CCBS)和安全區間路徑規劃(TO-AA-SIPP),旨在解決這些挑戰。CCBS算法通過在連續時間間隔上進行搜索,避免了時間離散化的問題,而TO-AA-SIPP算法則能夠處理動態障礙物環境中的任意角度路徑規劃。通過結合這兩種方法,AA-CCBS算法能夠在保證路徑最優性的同時,提高路徑規劃的效率。
此外,為了進一步提高算法的性能,論文引入了多約束(MC)和分離拆分(DS)技術。多約束技術通過添加多個約束來減少高層搜索迭代次數,而分離拆分技術則通過在沖突解決時添加正負約束來減少搜索工作量。這些技術的結合使得AA-CCBS算法在處理復雜路徑規劃問題時表現出色。
算法介紹
研究團隊提出了一種新的任意角度多智能體路徑規劃算法,稱為AA-CCBS(Any-Angle Continuous Conflict-Based Search)。該算法結合了連續沖突搜索(CCBS)和安全區間路徑規劃(TO-AA-SIPP),并通過引入多約束(MC)和分離拆分(DS)技術來提高算法的效率和效果。
連續沖突搜索(CCBS)
CCBS是沖突基搜索(CBS)的變體,適用于非離散時間線。它通過在連續時間間隔上進行搜索,避免了時間離散化的問題。CCBS的工作原理是為每個智能體單獨找到路徑,檢測這些路徑之間的沖突,并通過對個別智能體重新規劃來解決沖突。CCBS通過高層搜索選擇要約束的智能體,并通過低層搜索找到滿足約束的路徑。
安全區間路徑規劃(TO-AA-SIPP)
TO-AA-SIPP是SIPP(Safe Interval Path Planning)的變體,旨在為在動態障礙物環境中導航的智能體找到最優的任意角度路徑。TO-AA-SIPP的搜索節點由一個元組(頂點,安全時間間隔)標識,表示智能體可以在該時間間隔內安全地駐留在該頂點。與SIPP不同,TO-AA-SIPP不會通過擴展搜索節點來迭代構建搜索樹,而是預先生成所有搜索節點,并迭代嘗試識別節點之間的正確父子關系,以獲得最優解。
多約束(MC)
多約束技術通過添加多個約束來減少高層搜索迭代次數。論文提出了三種MC方法。
MC1:識別出所有源頂點相同的動作子集,并為每個智能體添加相應的多約束。盡管MC1方法有效,但在AA-MAPF中,互相沖突的動作數量可能很大,導致不安全區間過短,從而削弱約束效果。
MC2:為解決上述問題,MC2方法通過僅考慮有限的動作集和過濾掉導致原始不安全區間縮短的動作來增強約束效果。MC2方法在約束效果上更強。
MC3:進一步擴展MC2,包含不同源頂點但相同目標頂點的動作。這些動作可能導致相同智能體在幾乎相同位置發生碰撞,因此自然地包含在同一多約束中。
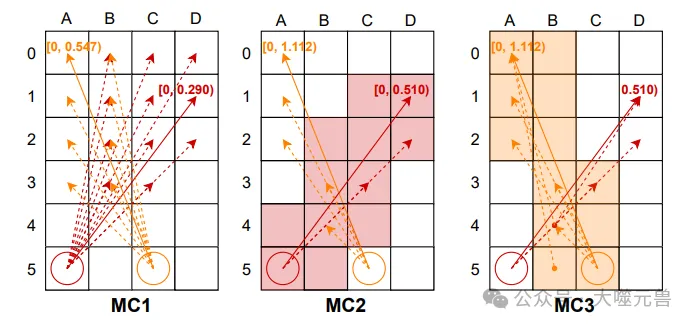
圖3:包含多約束的不同版本的動作。請注意,MC2和MC3中動作的時間間隔明顯大于MC1。因此,預計MC2和MC3將表現出更大的修剪能力。
分離拆分(DS)
分離拆分技術通過在沖突解決時添加正負約束來減少搜索工作量。一個CCBS子節點對智能體i添加負約束,另一個子節點對智能體i添加正約束并對智能體j添加負約束。論文提出了兩種實現方式:
直接使用DS:這種方式較為直接,通過在沖突解決時添加正負約束來減少搜索工作量。
結合MC使用DS:這種方式需要處理多個起點位置的連續搜索,較為復雜。為了簡化DS和MC的集成,論文建議避免將多約束作為地標,而是使用常規的負多約束。
通過結合這些技術,AA-CCBS算法能夠在保證路徑最優性的同時,提高路徑規劃的效率和效果。實驗結果表明,這些改進顯著提高了算法的性能,使其在處理復雜路徑規劃問題時表現出色。
實驗結果
為了評估AA-CCBS算法的性能,研究團隊在MovingAI基準測試中進行了廣泛的實驗。實驗使用了多個不同類型的地圖,包括空地圖、隨機地圖、迷宮地圖和倉庫地圖。每個地圖提供了25個場景,每個場景包含一組起點和目標位置。實驗通過逐步增加智能體數量,直到算法在300秒的時間限制內無法找到解決方案為止。
實驗結果顯示,AA-CCBS算法的多種變體在不同場景下表現出色。具體來說,MC3、DS和DS+MC3變體顯著優于其他變體。MC3在快速解決簡單實例方面表現尤為突出,而DS和DS+MC3在處理復雜實例時表現更佳。
在評估有界次優AA-CCBS時,研究團隊使用了不同的次優性界限(w = 1.01, 1.1, 1.25)進行實驗。結果表明,MC3在尋找有界次優解時顯著提高了AA-CCBS的性能,而DS變體未能超越原始AA-CCBS。這可能是因為DS的正約束在次優搜索中效果較差,不能立即消除沖突,而MC3通過對更多動作施加約束,在貪婪搜索中更有效地消除沖突。
具體實驗結果如下:
- 覆蓋率:MC3、DS和DS+MC3變體在300秒時間限制內解決了更多的實例。MC3在快速解決簡單實例方面表現尤為突出,而DS和DS+MC3在處理復雜實例時表現更佳。
- 解決時間:MC3在次優性界限較小時(w = 1.01)表現最佳,而DS和DS+MC3在次優性界限較大時(w = 1.25)表現更佳。這表明MC3適合快速解決較容易的實例,而DS和DS+MC3更適合解決較難的實例。
- 高層迭代次數:在解決不同MAPF問題實例時,MC3需要的高層迭代次數較少,尤其是在較容易的實例中。DS和DS+MC3在較難的實例中表現更佳,盡管需要更多的高層迭代次數。
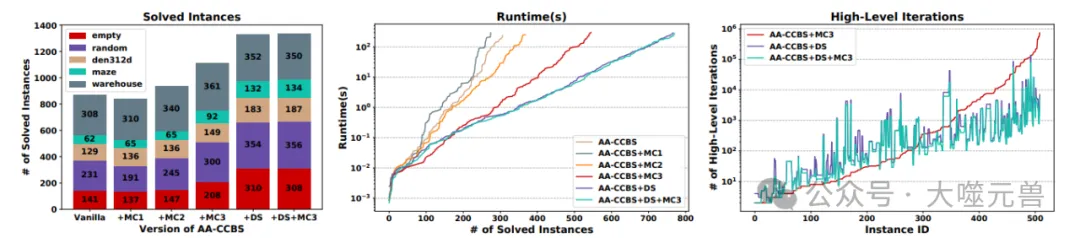
圖4:AA-CCBS不同變體的評估。左側窗格顯示了AA-CCBS每個版本在5分鐘時間限制內完全解決的實例數量。中間窗格顯示了找到解決方案所需的時間(Y軸以對數刻度表示)。
每個數據點告訴算法在一定時間內(Y軸)能夠解決多少個實例(X軸)。右側面板展示了解決不同MAPF問題實例所需的高級迭代次數。X軸顯示實例id。每個數據點告訴算法(Y軸)對特定問題實例(X軸)進行了多少次高級迭代。
實驗結果表明,AA-CCBS算法及其增強版本在處理任意角度多智能體路徑規劃問題時表現出色。MC3在快速解決簡單實例和尋找有界次優解方面表現尤為突出,而DS和DS+MC3在處理復雜實例時表現更佳。這些結果驗證了多約束和分離拆分技術在提高算法性能方面的有效性。
有界次優AA-CCBS
在實際應用中,找到最優解往往需要耗費大量時間和計算資源。為了在保證解的質量的同時提高算法的效率,論文提出了有界次優(Bounded Suboptimal, BS)AA-CCBS算法。該算法通過允許解的成本在最優解成本的某個倍數范圍內,從而在一定程度上放寬了最優性的要求,以換取更快的求解速度。
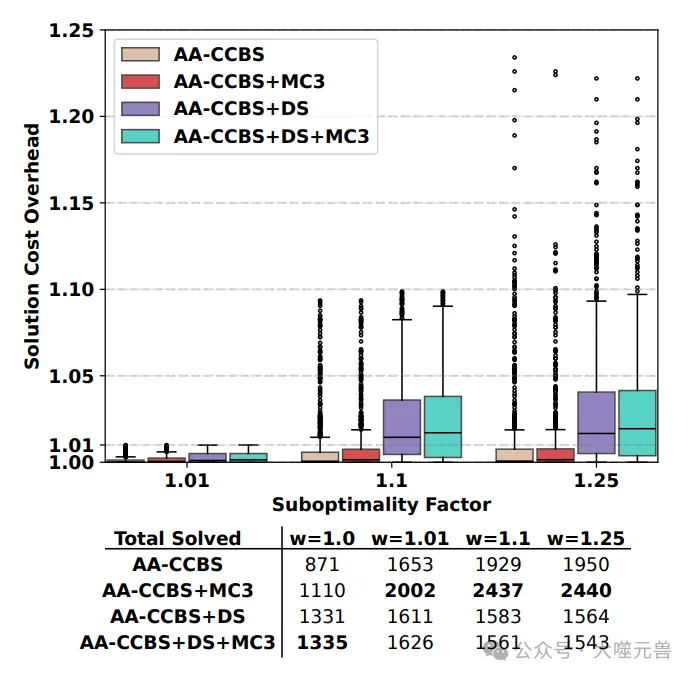
圖5:AA-CCBS的評估結果及其在不同次優因素下的修改。
實現方法
有界次優AA-CCBS的實現基于在高層搜索中引入焦點搜索(Focal Search)。具體來說,在每次高層迭代中,算法會創建一個名為FOCAL的節點列表。FOCAL包含所有生成的節點,這些節點的成本不超過 ( w \cdot f_{\text{min}} ),其中 ( w ) 是次優性界限, ( f_{\text{min}} ) 是常規AA-CCBS將擴展的節點的成本。
在FOCAL中,算法選擇沖突最少的節點進行擴展,并在節點數量相同時優先選擇約束更多的節點。這種方法迫使搜索更貪婪地解決沖突,同時保持所需的次優性界限。
實驗結果
研究團隊對BS AA-CCBS進行了廣泛的實驗,評估了不同次優性界限( ( w = 1.01, 1.1, 1.25 ) )下的算法性能。實驗結果顯示:
- 覆蓋率:MC3在尋找有界次優解時顯著提高了AA-CCBS的性能,而DS變體未能超越原始AA-CCBS。這可能是因為DS的正約束在次優搜索中效果較差,不能立即消除沖突,而MC3通過對更多動作施加約束,在貪婪搜索中更有效地消除沖突。
- 解決時間:MC3在次優性界限較小時( ( w = 1.01 ) )表現最佳,而DS和DS+MC3在次優性界限較大時( ( w = 1.25 ) )表現更佳。這表明MC3適合快速解決較容易的實例,而DS和DS+MC3更適合解決較難的實例。
- 解決方案成本:MC3版本的解決方案成本溢出不超過2%,即使在次優性界限 ( w = 1.25 ) 時也是如此。這表明MC3在保持較低成本溢出的同時,顯著提高了算法的求解速度。
結論與未來工作
論文提出了第一個針對任意角度多智能體路徑規劃(AA-MAPF)的最優算法AA-CCBS,并通過引入多約束(MC)和分離拆分(DS)技術顯著提升了算法的性能。實驗結果表明,這些改進在處理復雜路徑規劃問題時表現出色,能夠有效地解決沖突并找到最優解。
具體來說,MC3在快速解決簡單實例和尋找有界次優解方面表現尤為突出,而DS和DS+MC3在處理復雜實例時表現更佳。這些結果驗證了多約束和分離拆分技術在提高算法性能方面的有效性。
未來工作可以從以下幾個方面進一步探索和改進。
多約束形成過程:探索更復雜和高效的多約束形成過程,以進一步提高算法的剪枝能力和搜索效率。
增量搜索技術:在任意角度低層搜索中適應增量搜索技術,以減少重復計算和提高求解速度。
實際應用場景:將AA-CCBS算法應用于更多實際場景,如自動駕駛、無人機編隊和智能交通系統,驗證其在真實環境中的性能和魯棒性。
算法優化:進一步優化算法的實現,減少計算資源的消耗,提高算法的可擴展性和適用性。
總之,研究團隊為任意角度多智能體路徑規劃提供了一種高效且實用的解決方案,具有重要的理論和實際意義。通過進一步的研究和改進,AA-CCBS算法有望在更多領域中得到廣泛應用,為復雜路徑規劃問題提供更優的解決方案。(END)
參考資料:https://arxiv.org/pdf/2404.16379
本文轉載自??大噬元獸??,作者: FlerkenS

















