多智能體路徑規劃（MAPF）是一個在共享環境中為多個智能體規劃無碰撞路徑的問題。傳統上MAPF問題主要在離散環境中研究，時間和空間都被離散化為固定的步長和網格。隨著實際應用需求的增加，如倉庫物流和自動駕駛車輛，研究逐漸轉向連續環境中的路徑規劃。在連續環境中，時間和空間都是連續的，智能體的運動需要考慮更復雜的運動學和動力學約束。

在離散環境中，MAPF問題通常通過圖模型來表示，智能體在圖的頂點之間移動，避免在同一時間步出現在同一頂點。然而在連續環境中，智能體的路徑需要表示為平滑曲線，避免在任何時間點發生碰撞。這種連續表示更符合實際應用場景，如機器人在復雜環境中的導航。

在連續環境中，時間和空間都是連續的，智能體的運動需要考慮更復雜的運動學和動力學約束。例如，車輛在路徑規劃中需要考慮加速度和轉彎半徑，以避免突然的方向變化帶來的不穩定性。這種連續表示更符合實際應用場景，如機器人在復雜環境中的導航。

9 月 18 日arXiv的 熱門論文《Multi-agent Path Finding in Continuous Environment》提出一種在連續環境中進行多智能體路徑規劃的新方法，以解決實際應用中的挑戰。研究提出了一種新的連續環境沖突基搜索（CE-CBS）算法，該算法結合了高層次搜索框架的沖突基搜索（CBS）和低層次路徑規劃的RRT*算法。通過這種方法，智能體能夠在連續時間和空間中規劃平滑的無碰撞路徑，滿足各種運動學約束。

研究的主要挑戰在于如何在連續環境中有效地解決智能體之間的沖突。傳統的離散算法在處理連續時間和空間時效率較低，因此需要新的算法來提高路徑規劃的效率和可靠性。CE-CBS算法通過結合RRT*和B樣條曲線平滑處理，展示了在實際應用中的潛力。

本研究由布拉格捷克技術大學信息技術學院的Kristyna Janovská和Pavel Surynek領導。Kristyna Janovská是該學院的研究員，主要研究領域包括多智能體系統、路徑規劃和連續環境中的智能體運動。Pavel Surynek是該學院的教授，研究領域涵蓋人工智能、多智能體系統、路徑規劃和優化算法。

他們的研究致力于開發新的算法和模型，以解決多智能體在連續環境中的路徑規劃問題，旨在提高路徑規劃的效率和可靠性。通過提出的連續環境沖突基搜索（CE-CBS）算法，他們展示了在實際應用中的潛力，并為未來的研究方向提供了新的思路。

理論背景?

連續環境中的MAPF問題

在多智能體路徑規劃（MAPF）中，傳統的研究主要集中在離散環境中，即時間和空間都被離散化為固定的步長和網格。然而隨著實際應用需求的增加，如倉庫物流和自動駕駛車輛，研究逐漸轉向連續環境中的路徑規劃。在連續環境中，時間和空間都是連續的，智能體的運動需要考慮更復雜的運動學和動力學約束。

在離散環境中，時間通常表示為離散的時間步，環境則表示為圖的頂點和邊，智能體在圖的頂點之間移動，避免在同一時間步出現在同一頂點。然而在連續環境中，時間和空間都是連續的，智能體的路徑需要表示為平滑曲線，避免在任何時間點發生碰撞。這種連續表示更符合實際應用場景，如機器人在復雜環境中的導航。

為了應對連續環境中的MAPF問題，研究者們提出了多種算法。例如，連續沖突基搜索（CCBS）算法、擴展的增量沖突樹搜索（E-ICTS）算法和擴展的沖突基搜索-連續時間（ECBS-CT）算法。這些算法在處理連續時間和空間時表現出色，特別是CCBS算法，它無需時間離散化，直接在連續時間下工作，提供了更為精確的路徑規劃解決方案。

平滑連續MAPF（SC-MAPF）

平滑連續多智能體路徑規劃（SC-MAPF）問題是指在度量空間中找到一組平滑曲線，使得多個智能體在移動過程中不發生碰撞。SC-MAPF問題的定義如下：

• 路徑約束：路徑必須滿足一定的運動學約束，如最小角度約束，確保路徑段之間的角度不小于某個最小值。這是為了避免智能體在路徑上進行突然的方向變化，從而保證運動的平滑性和穩定性。
• 沖突定義：沖突定義為兩個智能體在某個時間段內重疊。解決沖突的方法是禁止智能體在沖突時間段內移動到特定曲線上。

在SC-MAPF問題中，智能體的路徑被定義為平滑曲線，這些曲線需要滿足一定的運動學約束，以確保智能體在移動過程中不會發生碰撞。例如，路徑段之間的角度必須大于某個最小值，以避免智能體在路徑上進行突然的方向變化。此外，智能體的路徑還需要考慮其物理尺寸和運動特性，以確保路徑的可行性和安全性。

通過引入平滑機制，如B樣條曲線，可以使路徑更加平滑，從而限制路徑的曲率，防止突然轉向變化。這不僅可以處理連續時間，還可以處理連續環境，考慮各種運動學或動力學約束，使得路徑規劃更加符合實際應用需求。

沖突基搜索（CBS）和連續時間沖突基搜索（CCBS）?

沖突基搜索（CBS）是一種用于多智能體路徑規劃（MAPF）的成本最優算法，主要應用于離散環境中。其基本原理是通過分層次的搜索框架來解決智能體之間的路徑沖突。CBS算法分為兩個層次：高層次和低層次。

在高層次，CBS算法首先為所有智能體計算初始路徑，然后檢查這些路徑是否存在沖突。沖突的定義是在同一時間步內，兩個或多個智能體出現在同一個頂點。如果發現沖突，算法會生成兩個新的約束，每個約束禁止其中一個沖突智能體在沖突時間步內進入沖突頂點。然后，算法將這兩個約束分別添加到兩個新的子問題中，并遞歸地解決這些子問題。

在低層次，CBS算法使用單智能體路徑規劃算法（如A*）為每個智能體計算路徑。路徑必須滿足高層次提供的約束，即智能體不能在特定時間步內進入特定頂點。通過這種方式，CBS算法能夠逐步解決沖突，找到一組無沖突的路徑。

CBS算法的優點在于其解決方案的成本最優性，即找到的路徑集的總成本最小。然而，由于其在離散環境中工作，時間和空間都被離散化為固定的步長和網格，這在處理實際應用中的連續環境時可能會遇到效率問題。

連續時間沖突基搜索（CCBS）算法是CBS算法的擴展，旨在解決連續時間下的多智能體路徑規劃問題。與CBS算法不同，CCBS算法在連續時間下工作，不需要將時間離散化為固定的時間步。

在CCBS算法中，沖突的定義和解決方式有所不同。由于時間是連續的，沖突不再僅僅是兩個智能體在同一時間步內出現在同一個頂點，而是兩個智能體在某個時間段內的路徑重疊。具體來說，CCBS算法定義了一個不安全時間間隔，如果一個智能體在這個時間間隔內到達沖突位置，則認為存在沖突。

CCBS算法的高層次和低層次操作與CBS算法類似，但在處理沖突時需要考慮連續時間。高層次仍然負責檢測沖突并生成約束，但這些約束現在包括不安全時間間隔。低層次則使用RRT*算法進行路徑規劃，確保路徑在連續時間和空間下無沖突。

結合RRT*算法和B樣條曲線平滑處理，CCBS算法能夠在連續環境中生成平滑的無沖突路徑。與CBS算法相比，CCBS算法在處理實際應用中的連續時間和空間時表現出更高的效率和可靠性。

快速擴展隨機樹（RRT）和RRT*?

RRT算法

快速擴展隨機樹（RRT）是一種用于路徑規劃的經典算法，特別適用于高維度的連續度量空間。RRT算法的基本概念是通過隨機采樣來構建一棵快速擴展的樹，從而探索路徑空間。其主要特點是能夠在復雜環境中高效地找到一條從起點到目標點的路徑。

RRT算法的工作原理如下：

初始化：從起點開始，創建一個包含起點的樹。

隨機采樣：在搜索空間中隨機生成一個點。

擴展樹：找到樹中距離隨機點最近的節點，并嘗試從該節點向隨機點擴展一條路徑。如果路徑不與障礙物相交，則將隨機點添加到樹中。

迭代：重復上述步驟，直到找到一條從起點到目標點的路徑，或者達到預設的迭代次數。

RRT算法的優點在于其簡單性和高效性，特別是在處理高維度和復雜環境時。然而，RRT算法生成的路徑通常不是最優的，可能包含許多不必要的繞行和急轉彎。

RRT*

為了克服RRT算法的不足，研究者們提出了RRT算法。RRT是RRT的改進版本，通過引入A*算法的成本函數，使得生成的路徑逐漸收斂到最優解。

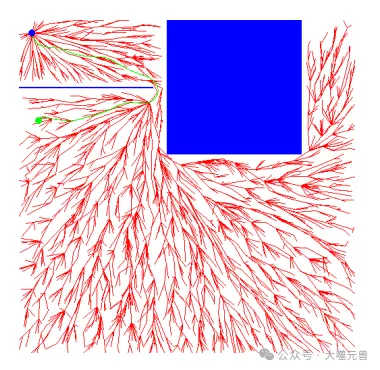
圖1：成功避開狹窄障礙物的平滑路徑。從藍色圓圈起始位置到綠色圓圈目標位置的結果路徑以綠色突出顯示。紅色顯示了采樣的RRT*樹。

RRT*算法的改進主要體現在以下幾個方面：

路徑優化：在每次擴展樹時，不僅考慮從最近的節點擴展路徑，還會檢查新節點是否可以通過其他路徑更優地連接到樹中。這種優化過程使得路徑逐漸接近最優解。

重連操作：在添加新節點后，RRT*會嘗試重新連接樹中的其他節點，以進一步優化路徑。這種重連操作可以消除不必要的繞行和急轉彎，使路徑更加平滑和高效。

RRT算法在路徑規劃中的優勢在于其能夠生成更優的路徑，同時保持RRT算法的高效性。通過結合路徑優化和重連操作，RRT能夠在復雜環境中找到更短、更平滑的路徑，適用于需要高精度路徑規劃的應用場景。

在連續環境中的多智能體路徑規劃中，RRT算法被廣泛應用于低層次路徑規劃。通過結合高層次的沖突基搜索（CBS）算法，RRT能夠在連續時間和空間中生成無沖突的平滑路徑，滿足各種運動學約束。

路徑平滑處理?

B樣條曲線

B樣條曲線是一種廣泛應用于計算機圖形學和路徑規劃中的數學工具。它是一種分段多項式曲線，通過一組控制點來定義曲線的形狀。B樣條曲線的一個顯著特點是它能夠生成平滑的曲線，這對于路徑規劃中的平滑處理尤為重要。

B樣條曲線的定義如下：

• 控制點：B樣條曲線由一組控制點定義，這些點決定了曲線的形狀。
• 節點向量：節點向量是一個非遞減序列，用于定義曲線的參數范圍。
• 基函數：B樣條基函數是分段多項式函數，用于計算曲線上的點。

通過這些元素，B樣條曲線可以表示為控制點和基函數的線性組合。具體來說，給定一組控制點和節點向量，B樣條曲線上的任意一點都可以通過基函數的加權和來計算。

路徑平滑算法

在多智能體路徑規劃中，路徑平滑處理是為了確保生成的路徑不僅無碰撞，而且平滑且符合運動學約束。使用B樣條曲線進行路徑平滑處理的步驟如下：

1. 路徑生成：首先，通過RRT算法生成初始路徑。RRT算法能夠在連續度量空間中高效地找到一條從起點到目標點的路徑，但生成的路徑可能包含許多急轉彎和不必要的繞行。
2. 控制點選擇：從RRT*生成的路徑中選擇一組關鍵點作為B樣條曲線的控制點。這些控制點通常是路徑上的轉折點或關鍵位置。
3. 曲線擬合：使用選定的控制點和節點向量，計算B樣條基函數，并通過基函數的加權和生成B樣條曲線。這個過程將初始路徑轉換為一條平滑的曲線。
4. 路徑插值：在生成的B樣條曲線上插值出更多的點，以確保路徑的平滑性和連續性。通常，每個路徑長度單位插值一個新點。
5. 路徑驗證：驗證生成的平滑路徑是否滿足所有運動學約束和避障要求。具體來說，需要檢查路徑上的每個點是否與障礙物相交，以及路徑段之間的角度是否滿足最小角度約束。
6. 調整和優化：如果生成的平滑路徑不滿足約束，可以調整控制點或節點向量，重新計算B樣條曲線，直到找到滿足要求的平滑路徑。

通過上述步驟，使用B樣條曲線進行路徑平滑處理，可以有效地生成符合實際應用需求的平滑路徑。這種方法不僅提高了路徑的可行性和安全性，還能夠顯著減少智能體在路徑上的急轉彎和不必要的繞行，從而提高路徑規劃的效率和可靠性。

提出的模型?

CE-CBS算法

連續環境沖突基搜索（CE-CBS）算法是本文提出的一種新方法，旨在解決連續環境中的多智能體路徑規劃問題。該算法結合了沖突基搜索（CBS）和快速擴展隨機樹（RRT*）算法，并通過B樣條曲線進行路徑平滑處理。

算法概述

高層次搜索：CE-CBS算法的高層次部分基于傳統的CBS算法。首先為所有智能體計算初始路徑，然后檢查這些路徑是否存在沖突。如果發現沖突，算法會生成新的約束，禁止沖突智能體在沖突時間段內進入沖突位置。

低層次搜索：在低層次部分，CE-CBS使用RRT算法進行路徑規劃。RRT算法通過隨機采樣和路徑優化，生成無沖突的路徑。與傳統的RRT*不同，CE-CBS在路徑規劃過程中考慮了連續時間和空間的約束。

路徑平滑處理：生成的路徑可能包含急轉彎和不必要的繞行。為了提高路徑的平滑性和可行性，CE-CBS使用B樣條曲線對路徑進行平滑處理。通過控制點和基函數的線性組合，生成平滑的曲線，確保路徑滿足運動學約束。

算法步驟

1. 初始化：從起點開始，為每個智能體生成初始路徑。
2. 沖突檢測：檢查所有智能體的路徑，檢測是否存在沖突。如果存在沖突，生成新的約束。
3. 路徑規劃：使用RRT*算法為每個智能體重新規劃路徑，確保路徑滿足新的約束。
4. 路徑平滑：使用B樣條曲線對生成的路徑進行平滑處理，確保路徑平滑且無沖突。
5. 迭代：重復上述步驟，直到找到無沖突的平滑路徑。

通過這種方法，CE-CBS算法能夠在連續時間和空間中生成無沖突的平滑路徑，適用于實際應用中的復雜環境。

智能體模型

在CE-CBS算法中，智能體被定義為具有固定半徑和速度的圓形物體。智能體在已知環境中移動，避開靜態和動態障礙物。具體來說，智能體模型包括以下幾個方面。

智能體定義：智能體被定義為具有固定半徑和速度的圓形物體。智能體的初始位置和目標位置在環境中預先設定。

運動學約束：智能體的路徑必須滿足一定的運動學約束，如最小轉彎半徑和最大加速度。這些約束確保智能體在路徑上移動時不會發生突然的方向變化，從而保證運動的平滑性和穩定性。

避障策略：智能體在路徑規劃過程中需要避開靜態和動態障礙物。靜態障礙物是環境中的固定物體，如墻壁和家具。動態障礙物是其他智能體，它們在環境中移動，可能與當前智能體發生碰撞。

路徑驗證：生成的路徑需要經過驗證，確保路徑段之間的角度滿足最小角度約束，路徑上的每個點都不與障礙物相交。如果路徑不滿足約束，需要重新規劃和調整，直到找到滿足要求的路徑。

通過結合RRT*算法和B樣條曲線平滑處理，CE-CBS算法能夠生成符合實際應用需求的平滑路徑。智能體在已知環境中移動，避開靜態和動態障礙物，確保路徑的可行性和安全性。

實驗結果?

實驗設置

為了驗證CE-CBS算法在連續環境中的性能，研究團隊設計了一系列實驗，測試不同參數設置和場景類型下的模型表現。實驗主要關注以下幾個參數。

• RRT*的最大節點數（ηmax）：這是RRT算法在路徑規劃過程中能夠采樣的最大節點數。較大的ηmax值允許RRT更深入地探索環境，但也會增加計算時間。
• 路徑段之間的最小角度值（α）：這是路徑段之間的最小允許角度，用于確保路徑的平滑性和可行性。較大的α值可以避免急轉彎，但可能會增加路徑長度。
• 智能體半徑（r）：這是智能體的物理尺寸，影響智能體在路徑規劃過程中避開障礙物和其他智能體的能力。

實驗場景包括不同大小和復雜度的環境，包含靜態和動態障礙物。智能體的起點和目標位置在環境中隨機分布，以模擬實際應用中的多種情況。

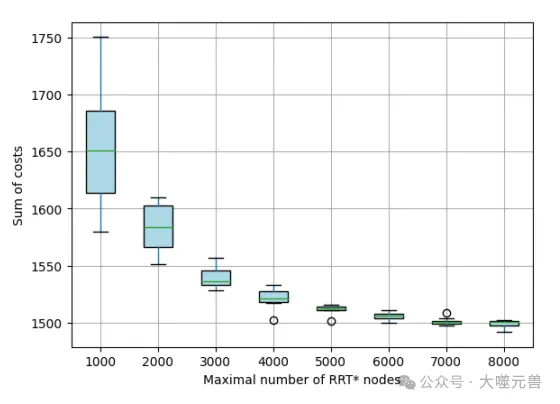
圖2：顯示每個代理的平均路徑長度與ηmax之間關系的實驗結果圖。

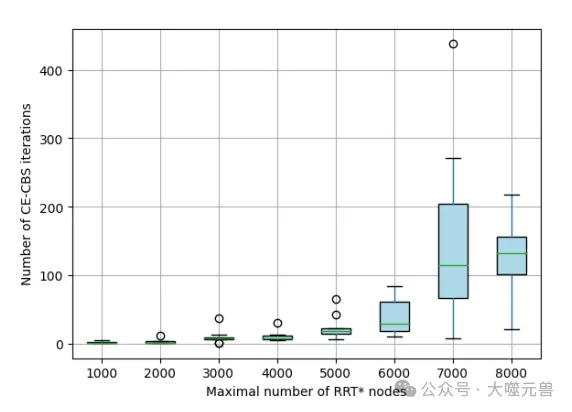
圖3：顯示CE-CBS迭代次數如何根據不同的ηmax而變化的圖。

實驗結果分析

實驗結果顯示，隨著ηmax的增加，路徑質量顯著提高。較大的ηmax值允許RRT*更深入地探索環境，生成更接近最優的路徑。然而較大的ηmax值也增加了計算時間，特別是在復雜環境中。實驗還發現，當ηmax超過一定值（如5000）后，路徑質量的提升變得不明顯，但計算時間顯著增加。因此，在實際應用中，需要在路徑質量和計算時間之間找到平衡。

圖 6：不同設置參數ηmax的運行結果比較——樣本RRT*節點的最大數量。

實驗表明，較大的α值可以有效避免路徑中的急轉彎，提高路徑的平滑性和可行性。然而，較大的α值也可能導致路徑長度增加，因為智能體需要繞過更多的障礙物。實驗結果顯示，當α值在90度左右時，路徑質量和計算時間之間的平衡效果最佳。

實驗結果顯示，隨著智能體半徑r的增加，路徑成本總和也隨之增加。較大的智能體需要更長的繞行路徑以避免與障礙物和其他智能體發生碰撞。實驗還發現，較大的智能體半徑可以減少路徑規劃中的沖突次數，因為智能體需要保持更大的安全距離，從而減少了搜索空間。

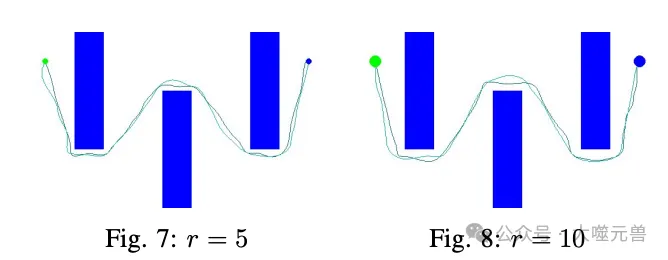
圖9：不同設置參數r-代理半徑的運行結果比較。

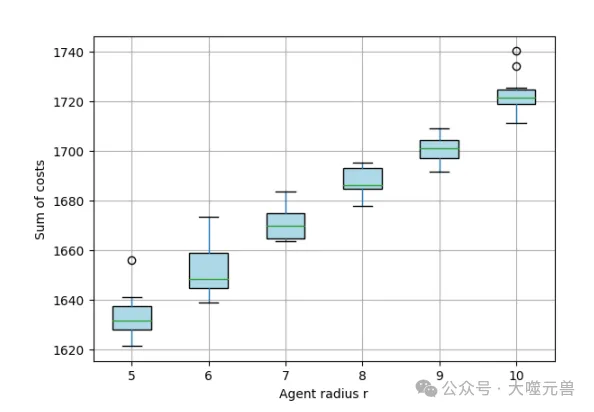
圖10：關于試劑半徑r的實驗結果。

CBS與CE-CBS比較

為了評估CE-CBS算法在連續環境中的優勢，研究團隊將其與標準CBS算法進行了比較。實驗設置為將連續環境轉換為2D網格，使用A*作為低層算法的標準CBS進行比較。結果顯示，CE-CBS算法在連續環境中表現出顯著優勢。

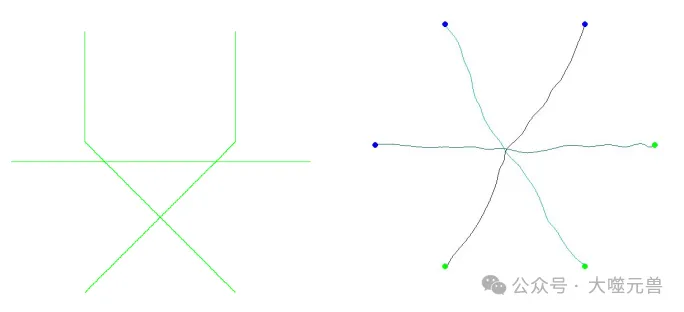
圖11：使用離散CBS（左）和連續CE-CBS（右）規劃的路徑。

路徑質量：CE-CBS算法生成的路徑更短、更平滑，因為它不受網格移動限制。實驗結果顯示，CE-CBS算法在所有測試案例中都找到了無沖突的解決方案，而標準CBS算法在某些情況下未能解決時間沖突。

計算時間：盡管CE-CBS算法在某些情況下需要更多的計算時間，但其生成的路徑質量顯著提高，特別是在復雜環境中。實驗結果表明，CE-CBS算法在處理連續時間和空間時表現出更高的效率和可靠性。

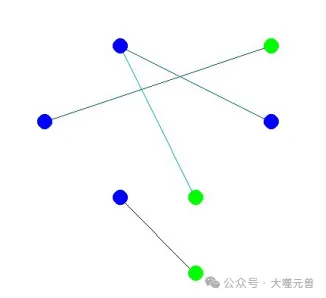
圖12:CE-CBS在地圖4×4網格上，4個代理從藍色位置開始，綠色目標位置。

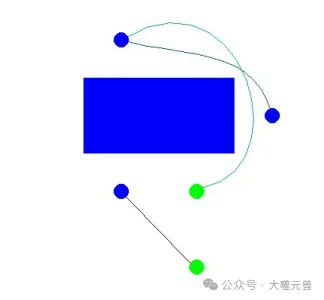
圖13:CE-CBS在地圖4×4網格上，一個矩形障礙物阻擋了兩個單元和三個代理。

從實驗結果來看，CE-CBS算法在連續環境中的多智能體路徑規劃中展示了顯著的優勢，能夠生成高質量的無沖突路徑，適用于實際應用中的復雜環境。

討論?

在實驗中，不同參數對CE-CBS算法的解決方案質量和計算時間產生了顯著影響。

RRT*的最大節點數（ηmax）

隨著ηmax的增加，RRT算法能夠更深入地探索環境，生成更接近最優的路徑。然而，當ηmax超過一定值（如5000）后，路徑質量的提升變得不明顯。這是因為RRT在較大搜索空間中已經找到了接近最優的路徑，進一步增加節點數對路徑質量的影響有限。

較大的ηmax值顯著增加了計算時間，特別是在復雜環境中。實驗結果顯示，隨著ηmax的增加，CE-CBS算法的迭代次數和計算時間也相應增加。因此，在實際應用中，需要在路徑質量和計算時間之間找到平衡。

路徑段之間的最小角度值（α）

較大的α值可以有效避免路徑中的急轉彎，提高路徑的平滑性和可行性。實驗表明，當α值在90度左右時，路徑質量和計算時間之間的平衡效果最佳。

較大的α值可能導致路徑長度增加，因為智能體需要繞過更多的障礙物。然而，這種增加是可以接受的，因為它顯著提高了路徑的平滑性和智能體的運動穩定性。

智能體半徑（r）

隨著智能體半徑r的增加，路徑成本總和也隨之增加。較大的智能體需要更長的繞行路徑以避免與障礙物和其他智能體發生碰撞。

較大的智能體半徑可以減少路徑規劃中的沖突次數，因為智能體需要保持更大的安全距離，從而減少了搜索空間。這種減少沖突的效果在復雜環境中尤為明顯。

CE-CBS算法在不同類型的環境中展示了良好的適應性，特別是在狹窄通道和多沖突區域中的導航能力。

狹窄通道

在狹窄通道中，智能體需要精確地規劃路徑，以避免與障礙物發生碰撞。CE-CBS算法通過結合RRT*和B樣條曲線，能夠生成平滑且無沖突的路徑，確保智能體在狹窄通道中順利導航。

在狹窄通道中，智能體之間的沖突更容易發生。CE-CBS算法通過高效的沖突檢測和解決機制，能夠及時發現并解決沖突，確保智能體的安全移動。

多沖突區域

在多沖突區域中，智能體需要頻繁調整路徑以避免與其他智能體發生碰撞。CE-CBS算法通過動態調整RRT*的最大節點數和路徑段之間的最小角度值，能夠靈活應對復雜環境中的多種沖突情況。

盡管多沖突區域增加了路徑規劃的復雜性，CE-CBS算法仍然能夠在合理的計算時間內找到無沖突的路徑。實驗結果表明，CE-CBS算法在處理多沖突區域時表現出較高的計算效率和路徑質量。

總體而言，CE-CBS算法在不同類型的環境中展示了良好的適應性和魯棒性，能夠有效解決連續環境中的多智能體路徑規劃問題。通過合理調整參數，CE-CBS算法能夠在保證路徑質量的同時，顯著提高計算效率，適用于實際應用中的復雜場景。（END）

?參考資料：???https://arxiv.org/pdf/2409.10680??

本文轉載自??大噬元獸??，作者： FlerkenS ????