ICLR 2024 Spotlight | 無懼中間步驟,MUSTARD可生成高質量數學推理數據
近年來,大型語言模型(LLM)在數學應用題和數學定理證明等任務中取得了長足的進步。數學推理需要嚴格的、形式化的多步推理過程,因此是 LLMs 推理能力進步的關鍵里程碑, 但仍然面臨著重要的挑戰。
以往的研究工作,如思維鏈(CoT),揭示了中間步驟引導的有效性。然而,人工地去標注這樣的中間步驟需要花費大量人力和時間成本,而自動合成的數據也容易在正確性和人類易讀性上面出現問題。
本文中,來自香港城市大學、中山大學、華為諾亞方舟實驗室等機構的研究人員提出了一個統一的數學推理數據合成框架 MUSTARD,能夠生成大量的、正確的且人類可讀可理解的高質量數學推理數據。

- 論文題目:MUSTARD: Mastering Uniform Synthesis of Theorem and Proof Data
- 論文鏈接:https://openreview.net/forum?id=8xliOUg9EW
- 代碼鏈接:https://github.com/Eleanor-H/MUSTARD
- 數據集鏈接:https://drive.google.com/file/d/1yIVAVqpkC2Op7LhisG6BJJ_-MavAMr1B/view
- 作者主頁:https://eleanor-h.github.io/
利用形式化證明器的高質量數據合成框架
MUSTARD 框架由三階段組成:
第一階段,概念采集:首先定義并建立了一個數學概念庫,涵蓋小學、初中、高中和高等教育四個教育階段的概念,每個教育階段有 5 至 9 個數學領域,涵蓋代數和幾何等不同類型的數學問題。每個領域都包含細分的數學概念,如多項式運算或因式分解。隨后從數學概念庫當中抽取一個或多個數學概念作為種子,規定所生成的問題類別。
第二階段,數據生成:根據數學概念提示大型語言模型生成數學問題和多步的求解過程。具體來說,MUSTARD 利用大型語言模型生成自然語言和代碼的能力,提示大型語言模型完成三項任務:(T1)生成與給定概念相關的數學問題;(T2)用自然語言給出問題的求解;(T3)自動形式化,將自然語言求解轉化為 Lean 3 的形式化求解。
第三階段,形式化驗證:使用交互式的形式化定理證明器的驗證篩選出準確的求解過程。MUSTARD 將 Lean 3 的形式化求解輸送給 Lean 形式化驗證器后,如果定理證明器沒有返回錯誤信息,則相應的數據會被收集到有效集合中。否則,MUSTARD 會從定理證明器那里收集錯誤信息,并提示語言模型修改形式化求解。MUSTARD 會進行多輪驗證和自我糾正,直到獲得有效的形式化求解。
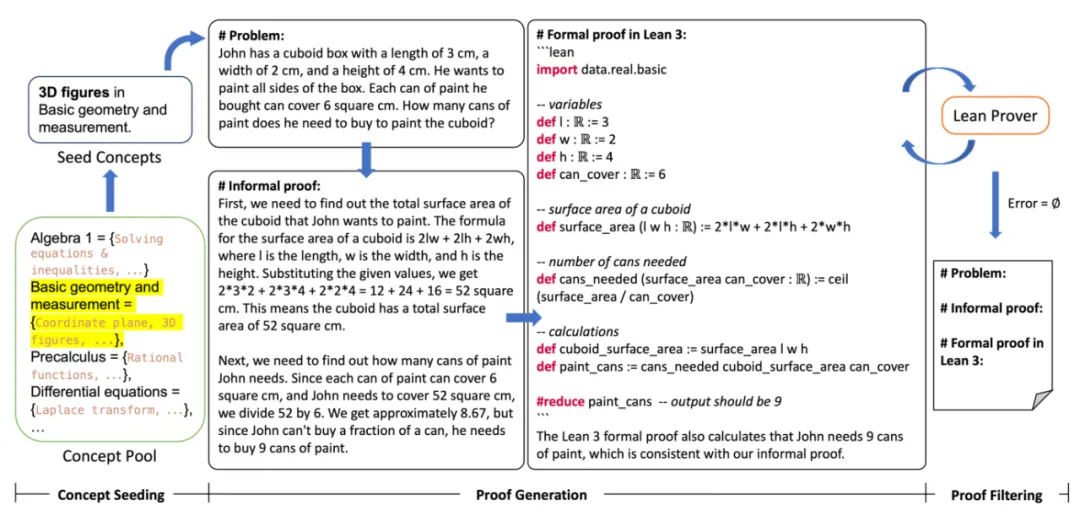
MUSTARD 框架由概念采集、數據生成、形式化驗證三階段組成。
數據質量的人工評價
為了探究 MUSTARD 生成數據的質量,研究團隊請掌握數學和 Lean 3 語言專業人士對數據進行了質量檢查。他們從生成的數據中隨機抽取 200 條,其中 100 條通過 Lean 定理證明器的驗證(有效組),100 條沒有通過驗證(無效組)。質量檢查涵蓋每條數據的四個部分(即自然語言問題描述、自然語言求解、形式化問題描述和形式化求解),包括了正確性和一致性的檢查。具體來說,高質量的數據應該有正確的自然語言問題描述 (D1) 和正確的問題求解 (D4)。形式化問題描述和求解應該與自然語言的問題描述和求解保持一致(D5、D6)。此外,數據應該符合指定的數學概念 (D2) 和問題類型 (D3)。表 3 展示了這六個檢查維度及要求。如果數據符合要求,則在維度中得 1 分,否則得 0 分。

表 3 顯示了有效組和無效組在每個維度上的準確率和相應的 p 值。(D1)和(D4)的顯著差異性說明了 MUSTARD 生成的問題和答案的正確性。(D6)的顯著差異性表明了所生成的數據的自然語言描述和形式化描述的高度一致性。
數據對模型數學推理能力的有效性
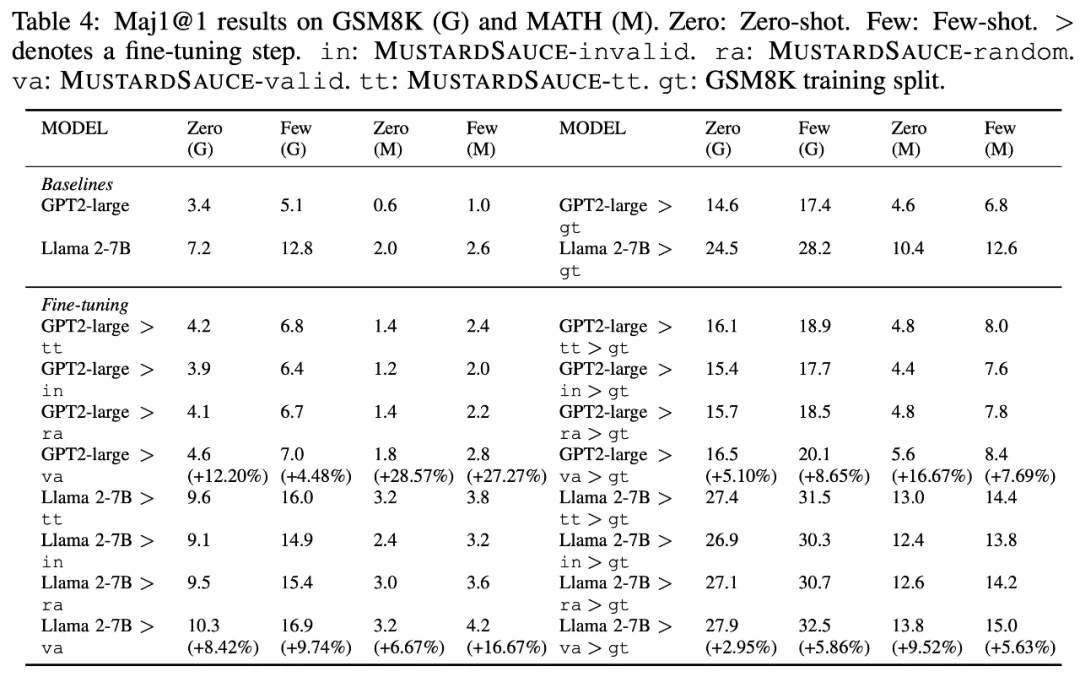
為了評估 MUSTARDSAUCE 對提高數學推理能力的影響,研究團隊利用這些數據對較小規模的語言模型進行了微調,并在數學應用題(MWP)和自動定理證明(ATP)上對其進行了評估。本文對比了 MUSTARDSAUCE 數據集的以下組合數據的有效性:
- MUSTARDSAUCE-valid:經過了 Lean 形式化證明器驗證的 5866 條數據;
- MUSTARDSAUCE-invalid:未能通過 Lean 形式化證明器驗證的 5866 條數據;
- MUSTARDSAUCE-random:隨機的 5866 條數據;
- MUSTARDSAUCE-tt:MUSTARD 生成的所有 28316 條數據。
研究團隊采用 LoRA [1] 在每個組合數據上微調開源 GPT2-large [2]、Llama 2-7B 和 Llama 2-70B [3]。對于數學應用題任務,他們使用 GSM8K [4] 和 MATH [5][6] 數據集進行評估。在評估自動定理證明時,研究團隊使用了 Mathlib [8]和 miniF2F [7] 基準。此外,他們也在 MUSTARDSAUCE-test 上進行了評估。
總的來說,在 MUSTARDSAUCE 上對模型進行微調提高了模型的數學推理能力。在自動定理證明(下表 5)和數學應用題求解(下表 4),使用 MUSTARDSAUCE-valid 進行微調與使用 MUSTARDSAUCE-random 進行微調相比,平均相對性能提高了 18.15%(下表 5)和 11.01%(下表 4)。
對于自動定理證明,經過微調的 Llama 2-7B 平均性能提升 15.41%,經過微調的 GPT 2-large 平均性能提升 20.89%。
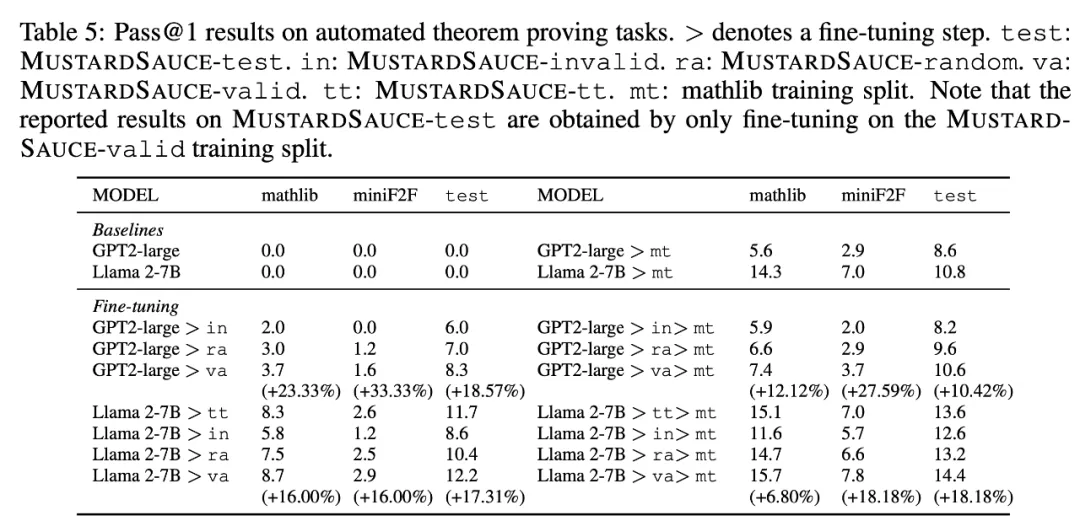
對于數學應用題求解,經過微調的 Llama 2-7B 平均性能提升 8.18%,經過微調的 GPT 2-large 平均性能提升 15.41%。此外,經過 MUSTARDSAUCE-tt 微調的模型雖在微調數據量上有絕對優勢,但其性能不及經過 MUSTARDSAUCE-valid 微調的模型性能。
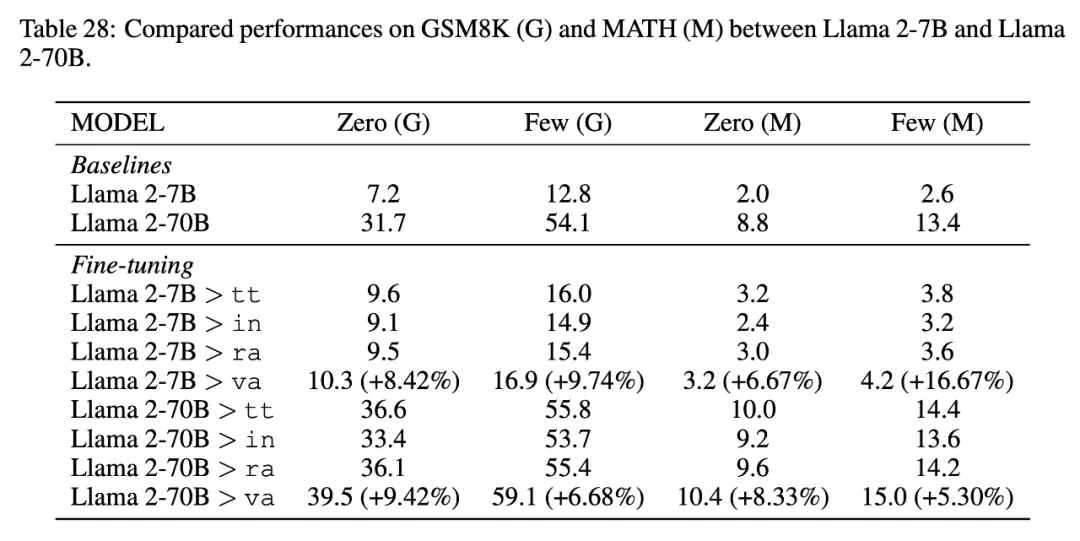
Llama 2-70B 的更多結果。在微調更大的語言模型時,MUSTARDSAUCE 數據仍然有效。
MUSTARDSAUCE 數據集
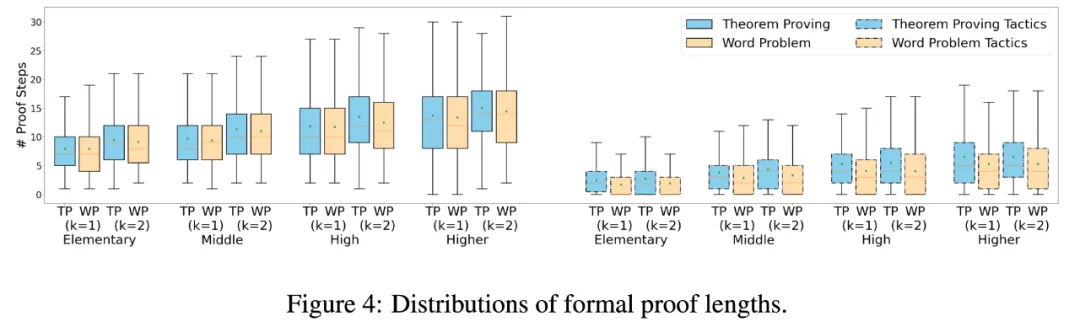
本文開源了 MUSTARDSAUCE 數據集。其中每一個數據都包含了自然語言的問題描述和多步求解,以及對偶的形式化語言 Lean 3 的問題描述和多步求解。MUSTARDSAUCE 的數據包括了數學應用題和定理證明題,涵蓋了從小學到高等教育階段的難度分級。題目的推理步數隨著題目難度的增長而增長。最難的題目需要 30 步左右的求解步驟,約 20 個 Lean 3 tactics。
數據集下載:https://drive.google.com/file/d/1yIVAVqpkC2Op7LhisG6BJJ_-MavAMr1B/view
自動形式化 / 非形式化挑戰賽
研究團隊還基于 MUSTARDSAUCE 數據集的自然語言和 Lean 形式語言的對偶數據,開放了一個自動形式化(autoformalization)和一個自動非形式化(auto-informalization)的挑戰賽。此外,研究團隊還同步開放了自動定理生成和證明(automated theorem generation and proving)和代碼輔助的運籌優化問題自動求解(automated optimization problem-solving with code)等兩個挑戰賽賽道。比賽時間為 2024 年 4 月 3 日 – 5 月 27 日。優勝隊伍將有機會參加 7 月 26 日于奧地利維也納舉辦的 ICML 2024 AI for Math 研討會。
- 賽道 1-1 (自動形式化):https://www.codabench.org/competitions/2436/
- 賽道 1-2 (自動非形式化):https://www.codabench.org/competitions/2484/
- 賽道 2 (自動定理生成和證明):https://www.codabench.org/competitions/2437/
- 賽道 3 (代碼輔助的運籌優化問題自動求解):https://www.codabench.org/competitions/2438/
本文轉自 機器之心 ,作者:機器之心

















